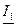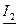Резонанс в электрических цепях

Резонансом в электрических цепях называется явление, когда цепь, содержащая реактивные элементы, ведет себя как чисто активная.

В электрических цепях могут наблюдаться 2 типа резонанса: резонанс токов и резонанс напряжений.

1. Резонанс напряжений наблюдается в цепях с последовательным соединением реактивных элементов.

Здесь ;

, где ;

, где .

, где ; .

В соответствии с определением резонанса, в электрической цепи при резонансе . При резонансе :

, где - резонансная частота данной цепи.

(Ом)

(Ом)

(Ом) – реактивное сопротивление при резонансе, волновое сопротивление данной цепи.

При резонансе:

При резонансе:

Таким образом, при резонансе .

- добротность контура

Например, если , то . j

- декремент затухания

Пусть

1

При резонансе:

Энергетически резонансную цепь можно представить в виде двух контуров: 1 контур содержит только резистор, а 2 контур содержит катушку индуктивности и конденсатор. В идеальном случае там будут происходить незатухающие колебания с частотой . За полпериода энергия будет накапливаться на катушке индуктивности, а в следующие полпериода – на конденсаторе.

2. Резонанс токов

, где

, где

, где ;

.

В соответствии с определением резонанса, в электрической цепи при резонансе .

, где - резонансная частота данной цепи.

( )

( )

, где - реактивные проводимости при резонансе.

Вывод: 1. При резонансе токов, который происходит при параллельном соединении реактивных элементов, проводимость всей цепи принимает минимальное значение .

2. Ток через резистор равен общему току .

3. Токи через реактивные элементы равны между собой, противоположны по фазе и в раз превышают входной ток.

Эквивалентная энергетическая схема выглядит следующим образом:

Резонанс в реальных цепях

При резонансе ( ).

- угол сдвига фаз между и , ;

- угол сдвига фаз между и , .

Определим резонансную частоту этой цепи:

Если , то . Подставив , определяем .

Мощность цепи переменного тока

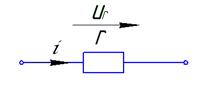
Пусть имеем двухполюсник

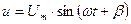
- мгновенная мощность

, где , - действующие значения переменного напряжения и тока.

Мощность в цепи переменного тока равна произведению действующих значений напряжения и тока на косинус угла между ними.

активная мощность, полезная мощность.

(ВАР – вольт-ампер-реактивная) – реактивная мощность.

( ) – полная мощность.

- полная мощность в комплексной форме.

,

или ,

или ,

Тема 5. Взаимоиндуктивность

Физические основы

Пусть имеем 2 катушки индуктивности, расположенные близко друг к другу.

Ток 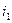, протекая по 1 катушке, создает магнитное поле.

_~

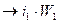_{~ ~} (магнитодвижущая сила) _~

_~

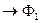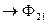В соответствии с правилом правого винта укажем направление магнитного потока.

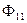- магнитный поток, охватывающий 1-ую катушку и созданный 1-ым током, т.е. первый индекс соответствует номеру катушки, а второй индекс – номеру тока.

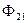- магнитный поток, охватывающий 2-ую катушку и созданный 1-ым током.

При переменном токе потоки тоже переменные, т.е. пульсируют. Начинает действовать закон электромагнитной индукции:

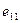- э.д.с. самоиндукции, т.е. э.д.с., наводимая в собственной катушке.

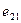- э.д.с. взаимоиндукции.

Пусть по 2-ой катушке протекает ток .

_~

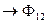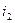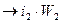_{~ ~} (магнитодвижущая сила) _~

_~

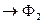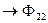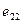- э.д.с. самоиндукции, т.е. э.д.с., наводимая в собственной катушке.

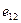- э.д.с. взаимоиндукции.

Таким образом, - э.д.с., наводимая в 1-ой катушке;

- э.д.с., наводимая во 2-ой катушке.

(18)

(Вб) – потокосцепление

(Гн) – индуктивность

Для линейной среды (магнитная проницаемость неизменная ) индуктивность для каждой катушки неизменна. Во сколько раз увеличивается ток, во столько же раз увеличивается потокосцепление.

(19)

Подставив соотношение (19) в уравнение (18), получим

Здесь , - индуктивности 1-ой и 2-ой катушек соответственно, т.е. ; .

, - взаимоиндуктивности между «1-ой и 2-ой» и «2-ой и 1-ой» катушками соответственно, т.е.

(Гн)

(Гн)

, так как пути замыкания магнитных потоков 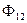и 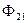одни и те же.

Уравнения индуктивно связанных между собой катушек

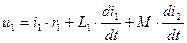
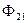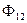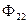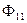Здесь магнитные потоки и имеют противоположное направление потокам и соответственно.

Для того чтобы определить суммироваться будут э.д.с. самоиндукции и э.д.с. взаимоиндукции или вычитаться, вводится понятие одноименных зажимов. Одноименными зажимами двух индуктивно связанных катушек называются такие, относительно которых токи, ориентированные одинаково, создают магнитные потоки в катушках одного направления. На схемах одноименные зажимы обычно помечаются.

В общем виде уравнение индуктивно связанных катушек для мгновенных значений имеет вид:

(20)

В комплексной форме эти уравнения имеют следующий вид:

(21)

Здесь