Расчет погрешности измерительных каналов
Любые измерения выполняются с ошибкой, т.е. с погрешностью – отклонением измеренного значения величины от ее истинного значения: ΔX = Xизм – X. Свой вклад в эту ошибку вносят:
• неидеальность метода измерений (эта составляющая полной погрешности называется методической погрешностью);
• неидеальность использованных технических средств (эта составляющая называется инструментальной или приборной погрешностью).
Важной технической характеристикой любых средств измерений, будь то линейка, градусник, датчик, АЦП или целый измерительный канал автоматизированной системы, является приписываемая им величина предельной инструментальной погрешности. Она характеризует предельное значение погрешности, которая может возникать при использовании данного средства измерения, и указывается в одной из трех форм:
1) абсолютной Δ = Xизм – X;
2) относительной γ = Δ/X;
3) приведенной δ =( Xmax – Xmin) × Δ× 100%
В качестве математической модели погрешности обычно принимается нормально распределенная случайная величина, которая может быть охарактеризована одним из двух способов:
1) как совокупность математического ожидания m (характеризующего систематическую составляющую погрешности) и дисперсии σ2 (характеризующей случайную составляющую); 2) в виде минимальной Δmin и максимальной Δmax границ возможных значений и доверительной вероятности Pдов попадания в этот интервал. Между двумя этими формами представления случайной величины существует простая связь:
• m = (Δmin+Δmax)/2; (4.1)
• Δ = Δmax-m = m-Δmin= K⋅σ, (4.2)
где K – некий коэффициент, зависящий от Pдов и выбираемый из таблицы квантилей нормального распределения (например, при Pдов=0.95 принимают K=1.96). Если средство измерений существует, то свойственная ему предельная погрешность измерений Δ определяется экспериментально в результате применения одного из двух методов (см. рис. 4.8). Именно эта характеристика указывается в документации на средство измерения
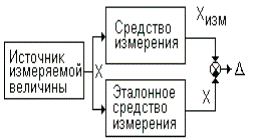
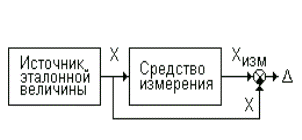
| а) Метод эталонного компонента | б) Метод источника эталонной величины |
Рис. 23. Два метода определения погрешности средств измерений
На этапе проектирования, когда средство измерений еще не существует, можно приближенно рассчитать свойственную ему погрешность измерений по известным характеристикам погрешности отдельных компонентов.
Первый способ расчета полной погрешности средства измерений заключается в том, что погрешности отдельных компонентов, пересчитанные на вход всей измерительной цепи, представляются в форме (m, σ2), а расчет характеристик суммарной погрешности выполняется по правилам:
• mΣ = m1+m2+…mM = Σ=M1ii m; (4.3)
• Σ=Σσ=σ++σ+σ=σM1i2i2M2221.... (4.4)
Второй способ расчета:
• ΔminΣ=Δmin1+Δmin2+…+ΔminM; (4.5)
• ΔmaxΣ=Δmax1+Δmax2+…+ΔmaxM. (4.6)
Первым способом обычно складываются основные, а вторым –дополнительные погрешности компонентов.
В нашем случае средствами измерения являются измерительные каналы автоматизированной системы. Рассчитаем их погрешности. Аппаратная часть обоих каналов имеет одинаковую структуру .
Для простоты расчетов предположим, что у всех компонентов систематическая составляющая погрешности пренебрежимо мала, т.е. равна нулю, а функции преобразования линейны.
Датчик измерения перемещений каретки имеет погрешность (разрешающую способность) Δ1=2 мм. В 12-разрядном АЦП с диапазоном измерения 0..10В погрешность дискретизации составляет h/2=(10В/4096)×0.5=0.0012В. Пересчитаем ее на вход датчика, т.е. определим, какое перемещение на входе датчика вызвало бы такое изменение напряжения у него на выходе. Для этого определим линейную функцию преобразования датчика Y=(10B/6000мм)⋅X=0.00167⋅X В/мм, следовательно, искомая погрешность на входе датчика составила бы Δ2= 0.0012/0.00167=0.73 мм. Считая, что K=1.96, в соответствие с (4.2), получаем θ1=Δ1/K=1.02 мм и θ2=Δ2/K=0.37 мм.
Таким образом, с.к.о. полной погрешности, согласно (4.4), составит θ=θ1+θ2= 1.086 мм, что, согласно (5), соответствует ΔΣИК1=K⋅θИК1=2.12 мм.
Датчик измерения биений вала имеет основную погрешность 3% от ширины диапазона измерения (0..5 мм), что составляет Δ1=0.15 мм. Погрешность дискретизации АЦП имеет порядок 10-4 мм и пренебрежимо мала, поэтому ΔΣИК2=0.15 мм.
Итак, можно сделать вывод, что рассчитанные характеристики погрешности измерительных каналов автоматизированной системы удовлетворяют требованиям, приведенным выше.
