Порядок выполнения работы. Определить количество информации (по Хартли), содержащееся в заданном сообщении

Определить количество информации (по Хартли), содержащееся в заданном сообщении, при условии, что значениями являются буквы кириллицы.

«Фамилия Имя Отчество» завершил ежегодный съезд эрудированных школьников, мечтающих глубоко проникнуть в тайны физических явлений и химических реакций

Построить таблицу распределения частот символов, характерные для заданного сообщения. Производится так называемая частотная селекция, текст сообщения анализируется как поток символов и высчитывается частота встречаемости каждого символа. Сравнить с имеющимися данными в табл 1.

На основании полученных данных определить среднее и полное количество информации, содержащееся в заданном сообщении. Оценить избыточность сообщения.

1. Построить таблицу распределения частот символов, характерныx для заданного сообщения путём деления количества определённого символа в данном сообщении на общее число символов

По формуле

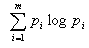
H= вычислил энтропию сообщения

2. Далее по формуле Шеннона для определения кол-ва информации

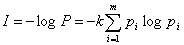вычислил кол-во информации в передаваемом сообщении

3. Вычислил избыточность D по формуле

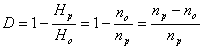
Отчет

Отчет должен быть оформлен в текстовом редакторе и содержать:

¾ наименование работы;

¾ цель работы;

¾ задание;

¾ последовательность выполнения работы;

¾ ответы на контрольные вопросы;

¾ вывод о проделанной работе.

Контрольные вопросы

1. Дать определение понятие энтропия?

2. Что означает вероятностный способ измерения информации?

3. Что означает статическое определение вероятности?

4. Запишите уравнение Хартли?

5. Какие основные разработки внес в основу теории информации Шеннон?

Расчет вероятностей Тема программы: Смысл энтропии Шеннона.

Тема: Составление закона распределения вероятностей.

Цель: научиться составлять законы распределения вероятностей.

Время выполнения: 2 часа

Оборудование: ПК.

Программное обеспечение: операционная система, калькулятор.

Теоретические основы

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными ненулевыми вероятностями. Число возможных значений может быть конечным или бесконечным (счетным).

Законом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей. Закон распределения может быть задан одним из следующих способов.

1. Таблицей

х	х1	х2	…	хn
р	р1	р2	…	pn

где .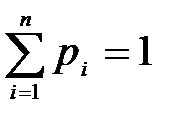

2. Аналитически 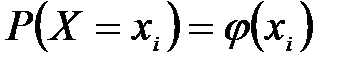. Например:

а) биномиальное распределение

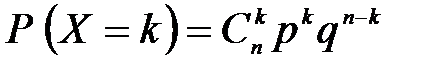, 0<р<1, k=0, 1, 2, …, n;

б) распределение Пуассона

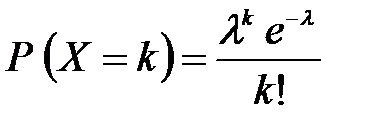, l>0, k=0, 1, 2, … .

3. С помощью функции распределения F(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т. е. .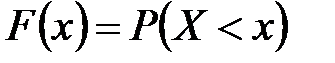

Свойства F(x):

1) ;

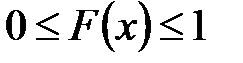2) 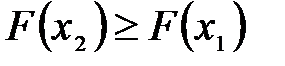, если ;

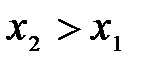3)

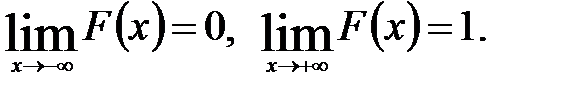
4. Закон распределения может быть задан графически - многоугольником распределения (см. пример 1).

Числовые характеристики дискретных случайных величин

Математическое ожидание ;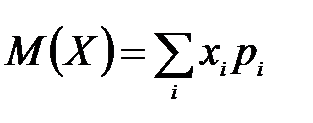

Дисперсия 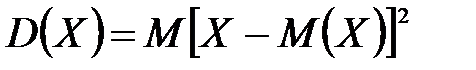или ;

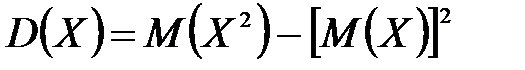Среднее квадратическое отклонение s(X)= .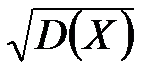

Для биномиального распределения М(X)=np, D(X)=npq. Для распределения Пуассона М(X)=l, D(X)= l.

Пример 1.

Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить её график. Найти М(X), D(X), s(X).

Решение: Дискретная случайная величина Х (число отказавших элементов в одном опыте) имеет следующие возможные значения: х₁=0 (ни один из элементов устройства не отказал), х₂=1 (отказал один элемент), х₃=2 (отказало два элемента) и х₄=3 (отказали три элемента).

Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1 (следовательно, q=1–0,1=0,9), получим: Р₃(0)=q³=0,9³=0,729;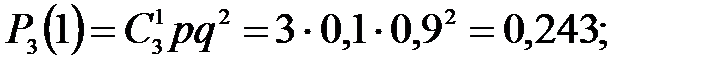

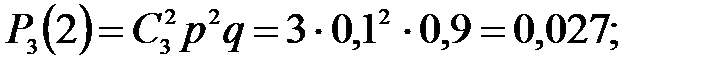
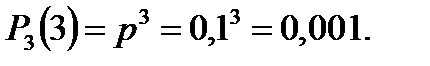
Контроль: 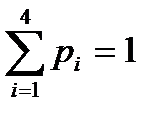; 0,729+0,243+0,027+0,001=1.

Искомый биномиальный закон распределения Х:

Х
р	0,729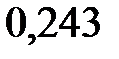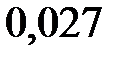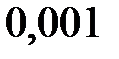

Для построения многоугольника распределения строим прямоугольную систему координат. По оси абсцисс откладываем возможные значения х_i, а по оси ординат – соответствующие им вероятности р_i. Построим точки М₁(0;0,729), М₂(1;0,243), М₃(2;0,027), М₄(3;0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения (Рис.1).

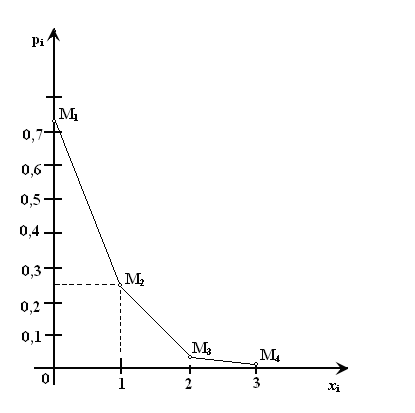
Рис.1

Найдем функцию распределения F(x)=Р(Х<х).

Для 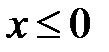имеем F(x)=Р(Х<0)=0;

для 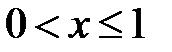имеем F(x)=Р(Х<1)=Р(Х=0)=0,729;

для 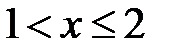F(x)=Р(Х<2)=Р(Х=0)+Р(Х=1)=0,729+0,243=0,972;

для 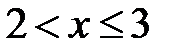F(x)=Р(Х<3)=Р(Х=0)+Р(Х=1)+ Р(Х=2)=0,972+0,027=0,999;

для х>3 будет F(x)=1, т. к. событие достоверно.

.

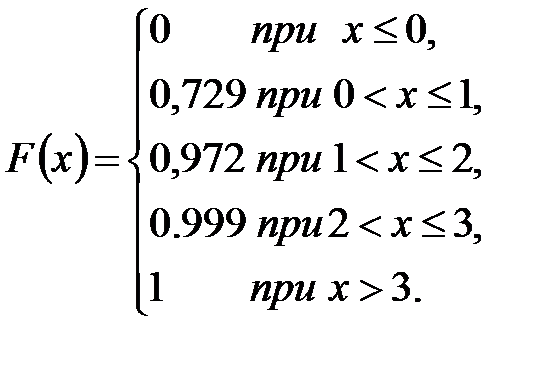График этой функции приведен на Рис. 2.

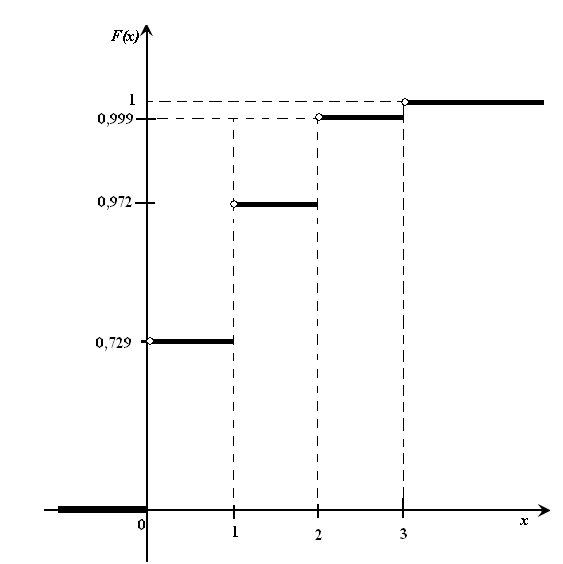
Рис. 2

Для биномиального распределения М(X)=np=3×0,1=0,3; D(X)=npq=3×0,1×0,9=0,27; s(X)= .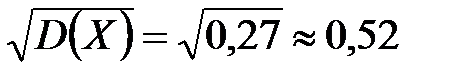

Пример 2.

В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения случайной величины X – числа стандартных деталей среди отобранных. Найти М(X), D(X).

Решение: Случайная величина Х – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: х₁=0; х₂=1; х₃=2. Найдем вероятности возможных значений Х по формуле (пример 2) 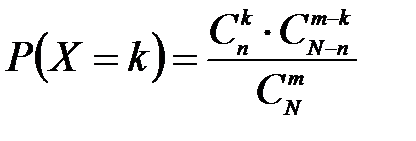(N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим: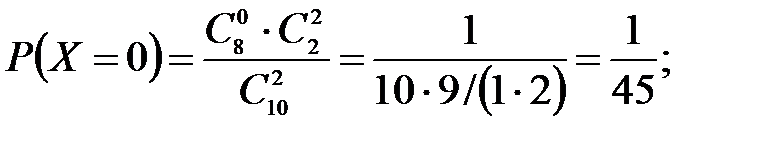

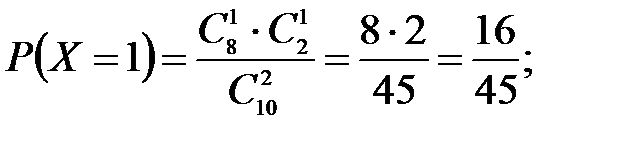
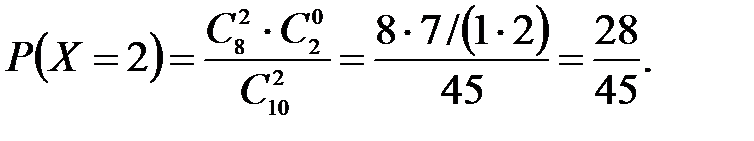
Составим искомый закон распределения:

Х
р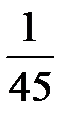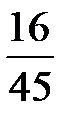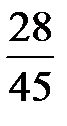

Контроль: 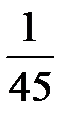+ + 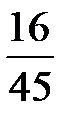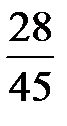=1.

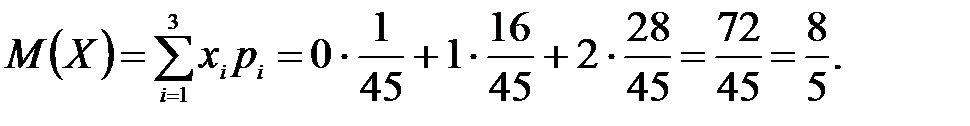
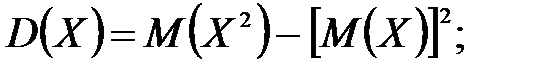
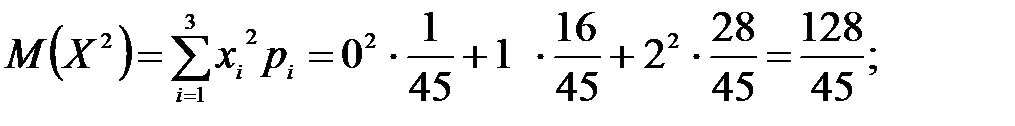
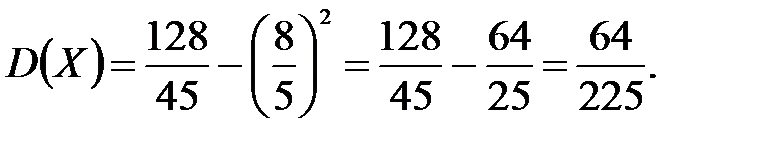
Пример 3.

В устройстве независимо друг от друга выходят из строя три элемента. Вероятность выхода из строя первого элемента – 0,3, второго – 0,2, третьего – 0,4. Составить закон распределения случайной величины Х – числа вышедших из строя элементов.

Решение: случайная величина Х имеет следующие возможные значения: х₁=0, х₂=1, х₃=2, х₄=3. р₁=0,3,q₁=1- р₁=0,7, р₂=0,2, q₂=1- р₂=0,8, р₃=0,4, q₃=1- р₃=0,6.

P(X=k) вычисляем по следующим формулам (см. пример 4) ;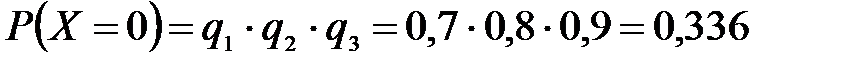

;

;

.

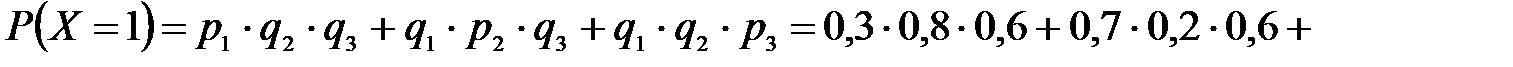
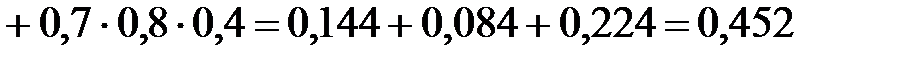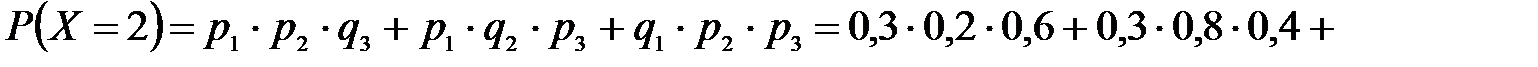
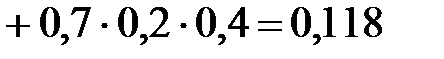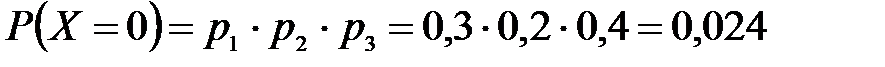Контроль: 0,336+0,452+0,118+0,024=1.

Х
р	0,336	0,452	0,118	0,024

Искомый закон распределения:

Пример 4.

Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно двум. Составить закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты. Найти М(X), D(X).

Решение: Поток заказов на такси можно считать простейшим, т. е. обладающим стационарностью, «отсутствием последствия» и ординарностью. Интенсивность потока (среднее число событий появляющихся в единицу времени) l=2. Вероятность появления k событий простейшего потока за время t=4 определяется формулой Пуассона 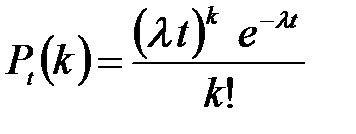, для данной задачи 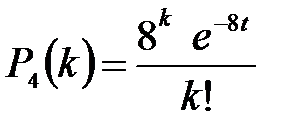. Совокупность возможных значений X есть счетное множество, т.е. х₁=0, х₂=1, … , х_k=k+1, …; тогда закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты принимает вид:

Х				…	k	…
р				…		…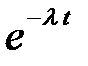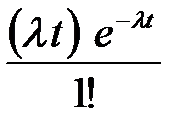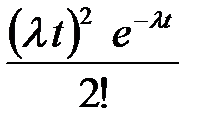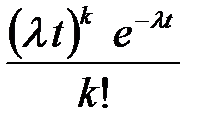

или

Х				…	k	…
р				…		…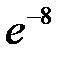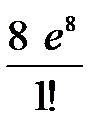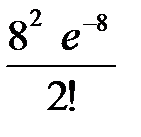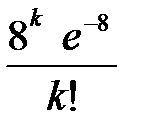

Воспользовавшись таблицей 3 приложения, окончательно получим:

Х				…	k	…
р	0,00035	0,002684	0,010735	…		…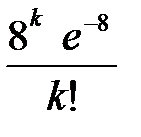

Наивероятнейшее число заказов такси за 4 минуты можно определить по получившемуся закону распределения ( значения х, при которых р максимально): k¢₀=7, k²₀=8. Для простейшего потока событий: математическое ожидание 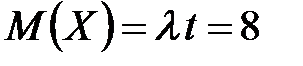, дисперсия .

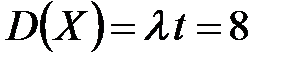Пример 5.

Y
р	0,2	0,5	0,3

Даны законы распределения независимых случайных величин X и Y. Составить закон распределения случайной величины Z=X+2Y. Найти М(Z), D(Z).

Х	-3
р	0,1	0,03	0,06

Решение: Закон распределения V=2Y получается из распределения Y путем умножения всех значений y_i на 2. Получаем:

V
р	0,2	0,5	0,3

.

Для составления закона распределения случайной величины Z вычислим все ее возможные значения по формуле , , .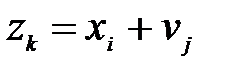

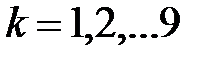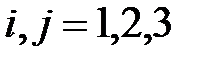Соответствующие данным значениям 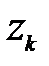вероятности 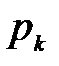можно вычислить по формуле умножения вероятностей 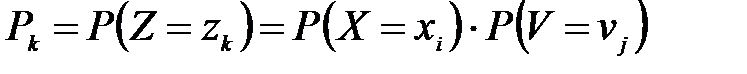, т. к. события 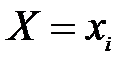и 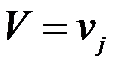- независимы (исходим из независимости случайных величин X и Y) и наступают совместно (событие { 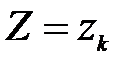} ={совместное наступление событи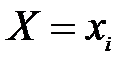й и 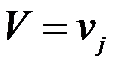}). Тогда распределение Z принимает вид

Z	-1
р	0,02	0,05	0,03	0,06	0,15	0.09	0,12	0,3	0,18

Рассмотрим значения 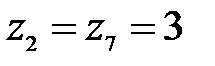. События 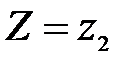и 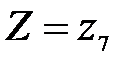несовместны, поэтому вероятность наступления хотя бы одного из этих событий вычисляется по правилу сложения вероятностей

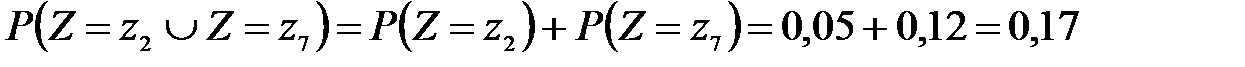
Искомый закон распределения случайной величины Z получается после размещения z_k по возрастанию.

Z	-1
р	0,02	0,06	0,17	0,15	0,3	0,03	0,09	0,18

Математическое ожидание M(Z) и дисперсию D(Z) можно найти по формулам:

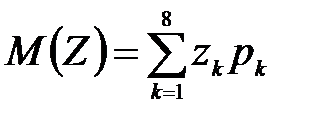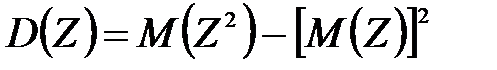; , где = .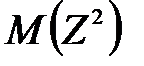

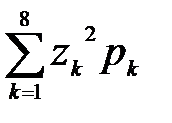Рассмотрим другой способ.

M(Z) и D(Z) можно найти через М(Х), М(Y), D(Х), D(Y).

,

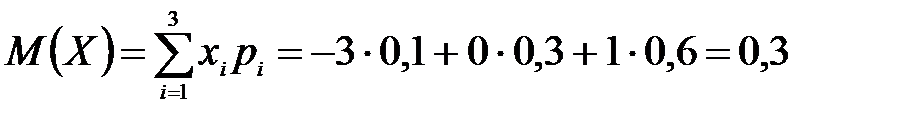
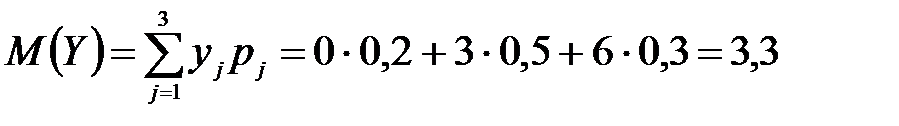
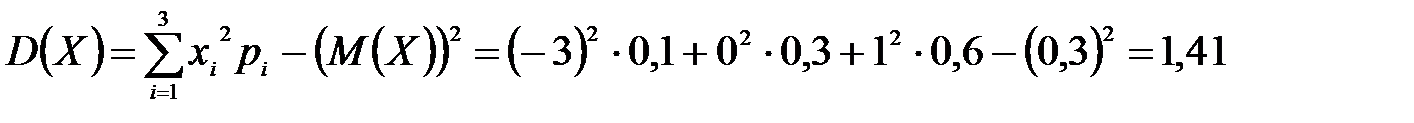
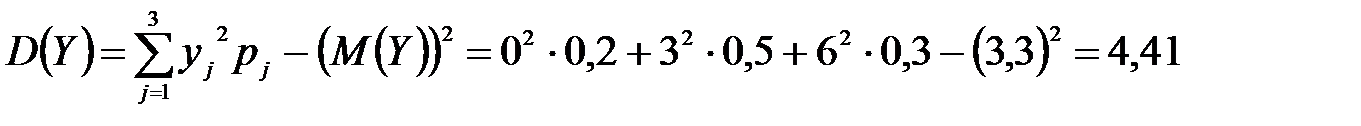
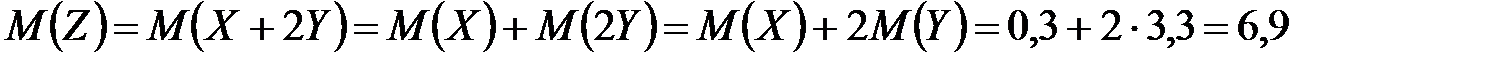т. к. математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания.

,

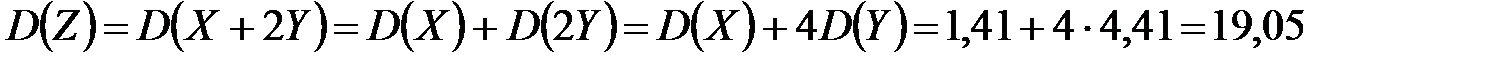т. к. дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых; постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Пример 6.

Стрелок ведет стрельбу с вероятностью попадания в цель 0,8 при каждом выстреле. Стрельба ведется до первого попадания, но делается не более 3 выстрелов. Составить закон распределения случайной величины Х, если: а) Х – число промахов; б) Х – число попаданий; в) Х – число произведенных выстрелов.

Решение: Вероятность попадания р=0,8; вероятность промаха q=1-p=0,2.

а) Случайная величина Х – число промахов при трех выстрелах – имеет следующие возможные значения: ; ; ; .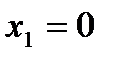

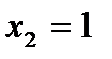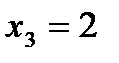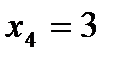Событие Х=0 равносильно попаданию с первой попытки, следовательно, Р(Х=0)=р=0,8.

Событие Х=1 равносильно попаданию со второй попытки, т. е. совместному наступлению двух событий: промаха и попадания; следовательно, Р(Х=1)=q р=0,2 0,8=0,16.

Событие Х=2 равносильно попаданию с третьей попытки, т. е. Р(Х=2)=q q р=0,2 0,2 0,8=0,032.

Событие Х=3 означает отсутствие попаданий, Р(Х=3)=q q q= 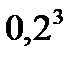=0,008.

Искомый закон распределения Х:

Х
р	0,8	0,16	0,032	0,008

б) Случайная величина Х – число попаданий – имеет следующие возможные значения: 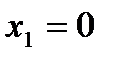(допущено три промаха); 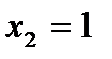(произошло попадание с первой, второй или третьей попытки).

Тогда Р(Х=0)= 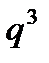= =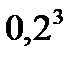0,008;

Р(Х=1)= р+q р+q q р=0,8+0,16+0,032=0,992

или Р(Х=1)=1-Р(Х=0)=1-0,008=0,992.

Искомый закон распределения Х:

Х
Р	0,008	0,992

в) Случайная величина Х – число произведенных выстрелов – имеет следующие возможные значения: ; ; .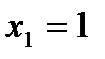

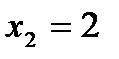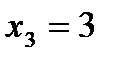Событие Х=1 равносильно попаданию с первой попытки, т. е. Р(Х=1)=р=0,8.

Событие Х=2 равносильно попаданию со второй попытки, т. е. Р(Х=2)=q р=0,16.

Событие Х=3 означает, что либо произошло попадание с третьей попытки, либо было три промаха. Тогда Р(Х=3)=q q р+q q q=0,032+0,008=0,04.

Искомый закон распределения Х:

Х
Р	0,8	0,16	0,04

Задачи

Вариант 1. Производятся последовательные независимые испытания приборов на надёжность. Каждый следующий прибор испытывается лишь в том случае, если предыдущий оказался надежным. Построить закон распределения случайного числа испытанных приборов, если вероятность выдержать испытание для каждого из них равна 0,9. Найти математическое ожидание числа испытанных приборов. Найти функцию распределения F(x) и построить ее график; найти М(X), s(X); построить многоугольник распределения.

Вариант 2. Известно, что в партии из 20 телефонных аппаратов 5 недействующих. Случайным образом из этой партии взято 4 аппарата. Построить закон распределения случайной величины Х – числа недействующих аппаратов из отобранных. Найти дисперсию этой случайной величины. В каких единицах она измеряется? Построить график функции распределения F(x) случайной величины Х, многоугольник распределения.

Вариант 3. Сырье на завод привозят от трех независимо работающих поставщиков. Вероятность своевременного прибытия сырья от первого поставщика равна 0,4, от второго – 0,7, от третьего – 0,6. Найти математическое ожидание М(X), дисперсию D(X) числа своевременных поставок сырья. Найти функцию распределения и построить ее график.

Вариант 4. Завод получает сырье на автомашинах от трех независимо работающих поставщиков. Вероятность прибытия автомашины от первого поставщика равна 0,2, от второго – 0,3 и от третьего – 0,1. Составить распределение числа прибывших автомашин. Найти математическое ожидание и дисперсию полученной величины. Построить график функции распределения F(x).

Вариант 5. Вероятность изготовления бракованной детали р=0,1. Изготовлено 4 детали. Х – случайное число бракованных деталей. Построить закон распределения случайной величины X, найти ее математическое ожидание и дисперсию. Построить график функции распределения, многоугольник распределения.

Вариант 6. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, ровно 2. Составить закон распределения случайной величины Х – числа заявок, поступивших за 3 часа. Найти М(X), D(X) и наивероятнейшее число заявок за 3 часа.

Вариант 7. В среднем в магазин заходит 3 человека в минуту. Составить закон распределения случайной величины Х – числа зашедших в магазин человек за 2 минуты. Построить многоугольник распределения. Найти М(X), D(X).

Вариант 8. Даны законы распределения независимых случайных величин

Х	-3
Р	0,1	0,3	0,6

Y
р	0,2	0,5	0,3

Составить законы распределения случайных величин:

а)XY; б) X+Y. Найти М(X+Y), D(X+Y). Справедливо ли равенство М(X)×М(Y)=М(X×Y)?

Вариант 9. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами Х₁ и Х₂ , которые характеризуются следующими законами распределения:

Х1
Р	0,3	0,4	0,3

Х2
Р	0,2	0,1	0,2	0,5

и

Результаты стрельбы одного стрелка не влияют на результат стрельбы другого. Составить закон распределения числа очков, выбиваемых командой, если стрелки сделают по одному выстрелу. Убедиться в справедливости равенства D(Х₁+Х₂)=D(Х₁)+D(Х₂).

Вариант 10. Производятся выстрелы из орудия с вероятностью попадания в цель 0,9 при каждом выстреле. Стрельба ведётся до первого попадания, но делается не более 4 выстрелов. Составить закон распределения случайной величины X, если: а) X – число произведенных выстрелов; б) X – число промахов; в) X – число попаданий. Найдите математическое ожидание всех найденных случайных величин.

Отчет

Отчет должен содержать:

¾ наименование работы;

¾ цель работы;

¾ задание;

¾ последовательность выполнения работы;

¾ ответы на контрольные вопросы;

¾ вывод о проделанной работе.

Контрольные вопросы

1. Какие значения не может принимать вероятность?

2. Чему равна вероятность достоверного события? Невозможного?

3. Дайте определение закону распределения дискретной случайной величины.

4. Дайте определение математическому ожиданию?

Практическое занятие № 9

Тема программы: Сжатие информации.

Тема: Системные требования алгоритмов сжатия. Алгоритмы сжатия данных неизвестного формата.

Цель: научиться сжимать информацию с помощью метода Хаффмана и метода RLE.

Время выполнения: 2 часа

Оборудование: ПК.

Программное обеспечение: операционная система, калькулятор, текстовый редактор.

Теоретические основы

Сжатие данных (англ. data compression) — алгоритмическое преобразование данных, производимое с целью уменьшения их объёма. Применяется для более рационального использования устройств хранения и передачи данных. Синонимы — упаковка данных, компрессия, сжимающее кодирование, кодирование источника. Обратная процедура называется восстановлением данных (распаковкой, декомпрессией). Сжатие основано на устранении избыточности, содержащейся в исходных данных. Простейшим примером избыточности является повторение в тексте фрагментов (например, слов естественного или машинного языка). Подобная избыточность обычно устраняется заменой повторяющейся последовательности ссылкой на уже закодированный фрагмент с указанием его длины. Другой вид избыточности связан с тем, что некоторые значения в сжимаемых данных встречаются чаще других. Сокращение объёма данных достигается за счёт замены часто встречающихся данных короткими кодовыми словами, а редких — длинными (энтропийное кодирование). Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал или белый шум, зашифрованные сообщения), принципиально невозможно без потерь. В основе любого способа сжатия лежит модель источника данных, или, точнее, модель избыточности. Иными словами, для сжатия данных используются некоторые априорные сведения о том, какого рода данные сжимаются. Не обладая такими сведениями об источнике, невозможно сделать никаких предположений о преобразовании, которое позволило бы уменьшить объём сообщения. Модель избыточности может быть статической, неизменной для всего сжимаемого сообщения, либо строиться или параметризоваться на этапе сжатия (и восстановления). Методы, позволяющие на основе входных данных изменять модель избыточности информации, называются адаптивными. Неадаптивными являются обычно узкоспециализированные алгоритмы, применяемые для работы с данными, обладающими хорошо определёнными и неизменными характеристиками. Подавляющая часть достаточно универсальных алгоритмов являются в той или иной мере адаптивными.

Все методы сжатия данных делятся на два основных класса:

· Сжатие без потерь

· Сжатие с потерями

При использовании сжатия без потерь возможно полное восстановление исходных данных, сжатие с потерями позволяет восстановить данные с искажениями, обычно несущественными с точки зрения дальнейшего использования восстановленных данных. Сжатие без потерь обычно используется для передачи и хранения текстовых данных, компьютерных программ, реже — для сокращения объёма аудио- и видеоданных, цифровых фотографий и т. п., в случаях, когда искажения недопустимы или нежелательны. Сжатие с потерями, обладающее значительно большей, чем сжатие без потерь, эффективностью, обычно применяется для сокращения объёма аудио- и видеоданных и цифровых фотографий в тех случаях, когда такое сокращение является приоритетным, а полное соответствие исходных и восстановленных данных не требуется.