Лекция 6. Образование и развитие трещин при работе конструкций АТ
Вопрос 1.Образование трещин при работе конструкций АТ
Как правило, абсолютное большинство отказов находится в причинно-следственной связи с нарушением целостности (появлением трещины) или разрушением какого-либо элемента конструкции. В последние годы много исследований посвящено кинетике разрушения (развитию трещин). Это связано с возможностью учета живучести конструкции.
В1909-1913 гг. были опубликованы работы русского и английского ученых о наличии пиковых напряжений по краям овальных отверстий в напряженной пластине (рис.10) Наиболее опасные пиковые напряжения наблюдаются в местах максимальной кривизны эллипса (точка А), а их количественные значения могут во много раз превышать 
. Тогда же впервые в практику расчетов на прочность вошло понятие «концентрация напряжений».
В 1921г. доказано, что концентрация напряжения в дефекте позволяет превращать энергию деформирования в энергию разрушения и что разрушение возможно лишь при постоянном подводе энергии (классическая концепция хрупкого разрушения). Данная концепция применима лишь к абсолютно непластичным металлам и используется в теории.
Рис. 10. Графическая интерпретация решения Колосова – Инглиса для напряженной пластины с эллиптическим отверстием
В концепции вязкости разрушения, пришедшей на смену классической концепции, учитываются такие явления, как текучесть, вязкость, ползучесть, т.е. учитывается энергия, затрачиваемая на развитие пластической деформации вблизи трещины. Эта концепция позволила выделить целую группу так называемых безопасных трещин.
Вопрос 2. Развитие трещин при работе конструкций АТ
Итак, существует определенная связь между нагрузкой и длиной трещины. Выявление такой связи обусловлено положением, что разрушение требует определенных затрат энергии (это положение Гриффитс обосновал в своей статье "Явление разрушения и течение твердого тела", опубликованной им в феврале 1920 г.).
Роль энергии в процессе хрупкого разрушения по Гриффитсу в следующем: концентрация напряжений у вершины трещины есть необходимое, но недостаточное условие развития трещины, нужно еще обеспечить подвод достаточной энергии к ее вершине. Поясним на примере.
Возьмем прямоугольную пластину, растянем ее напряжением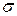 
и жестко закрепим края (рис. 11). Длину и ширину пластины считаем большими по сравнению с толщиной, которую для удобства принимаем равной единице: 
, . 
Определим энергию упругой деформации, запасенной в такой пластине. Для этого обратимся к типичной кривой деформирования (рис. 12).
Если в некоторый момент, соответствующий точке М, под действием силы 
удлинение 
увеличивается на 
, то совершается дополнительная работа 
(V – объем образца) и на столько же увеличивается энергия деформации. Следовательно, приращение энергии в единице объема 
. На рис 12 это приращение изображено заштрихованной площадью столбика с основанием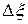 
. Таким образом, если например, при нагружении образца возникшая деформация соответствует деформации в точке В, то произведенная на единицу объема работа W равна площади фигуры ОВД. Она состоит из обратимой упругой энергии, равной площади треугольника ВСД, и необратимой работы пластических деформаций, изображаемой площадью ОВС. Для линейно-упругого материала, подчиняющегося закону Гука 
, удельная упругая энергия
,
поскольку геометрически это есть площадь прямоугольного треугольника с катетами BD и CD.
В закрепленной пластине (см. рис. 11) запасена энергия упругой деформации 
, в пересчете на единицу площади приходится энергия 
.
 |
Пусть в пластине появилась трещина малой длины 
. Эта трещина приведет к уменьшению деформаций в прилегающей зоне (на рис. 11 эта зона отмечена точками). Площадь зоны пропорциональна 
. Таким образом, освобожденная трещиной упругая энергия
.
Константу С, учитывающую неопределенность формы прилегающей к трещине зоны, Гриффитс определил из решения Колосова – Инглиса (см. рис. 10). Оказалось, что 
, тогда
.
Освобожденная упругая энергия затрачивается на разрушение, т. е. на образование новой поверхности тела. Если считать 
– удельную работу разрушения на единицу площади новой поверхности тела – постоянной материала, то работа, затрачиваемая на образование трещины длиной 
,
.
Итак, энергия, затрачиваемая на рост трещины, возрастает пропорционально , а высвобождаемая энергия деформации возрастает пропорционально 
. Это показано графически на рис. 13, где А – соответствует изменению энергии, затрачиваемой на рост трещины в зависимости от ее длины, а кривая В – высвобождающейся при этом энергии, накопленной при деформировании. Кривая С представляет собой алгебраическую сумму указанных двух энергий и характеризует энергетический баланс.
Вплоть до точки X в системе в целом преобладает поглощение энергии, за точкой X энергия начинает высвобождаться. Из этого следует, что существует некоторая критическая длина трещины 
. Трещины, длина которых меньше , как правило, не растут и являются безопасными; трещины, длина которых больше , при заданном напряжении распространяются самопроизвольно и на практике весьма опасны.
Рис. 13. Энергетическая модель разрушения по Гриффитсу
Запишем выражение для :
.
Заметим, что длина безопасной трещины обратно пропорциональна податливости – способности материала к упругому деформированию. В общем случае, чем больше податливость материала, тем меньше длина безопасной трещины. Например, резина при деформации запасает довольно много энергии, однако ее работа разрушения очень мала. Поэтому критическая длина трещины у растянутой резины невелика (для того, чтобы надутый воздушный шар мгновенно лопнул, достаточно наколоть его иголкой).
Процесс разрушения складывается из двух стадий – зарождения трещины и ее развития, причем каждая из этих стадий подчиняется своим законам, характеризуется своими критериями.
К основным критериям развития трещин в деформируемых металлах и сплавах относятся критерии интенсивности и вязкости разрушения 
и 
. Когда трещина развивается, то в более или менее обширной окрестности ее кончика всегда происходят необратимые пластические деформации материала.
Вязкость разрушения – определяемый экспериментально показатель материала, соответствующий критическому значению напряжения в вершине трещины, когда запасенной энергии деформации достаточно для распространения трещины. Величина зависит не только от толщины, но и от размера, формы трещины и типа нагружения (рис. 14). Критическая длина сквозной трещины в данном случае равна 10 мм, а несквозной дискообразной трещины – 23 мм.
Скорость развития трещины усталости (при многоцикловом нагружении) подчиняется зависимости Пэриса 
, где А и п – эмпирические коэффициенты; 
– перепад коэффициента интенсивности напряжений за цикл нагружения; N – число циклов.
Рис.14. Зависимость критической длины трещины от ее формы:
1 – сквозная трещина; 2 – трещина ограниченных размеров
Показатель степени n для разных металлов может иметь значение от 2 до 7 (чаще всего n = 4). Чем более хрупкий металл, тем больше показатель степени n. Формула Пэриса описывает средний (линейный) участок полной диаграммы усталостного разрушения (рис.15).
 |
Рис.15. Схема усталостного разрушения
ЛИТЕРАТУРА
1). Пивоваров В.А. Повреждаемость и диагностирование авиационных конструкций. – М.: Транспорт, 1994.
******************************************************************