Построение таблицы истинности заданной функции

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

Электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра вычислительной техники

отчет

По лабораторной работе №5

По дисциплине «Информатика»

Тема: «Использование пакета MicrosoftExcel
для работы с логическими функциями»

Студент гр. 5891		Агеев К.А.
Ассистент каф. ВТ		Бондаренко П.Н.

Санкт-Петербург, 2015

Содержание:

1 Цель работы.. 3

2 Основные теоретические положения. 3

3 Экспериментальные результаты. 3

3.1. Построение таблицы истинности заданной функции. 3

3.2Преобразование заданной функции. 5

3.3 Построение таблицы для упрощенной функции. 6

3.3 Сравнение таблиц истинности. 6

3.4 Представление функции в форме СДНФ. 6

3.5 Упрощение формы СДНФ. 7

4 Заключение. 8

Цель работы

Освоить основные приемы работы с логическими функциями пакета MS Excel, практически освоить изученные теоретические основы алгебры логики.

Для функции, заданной в виде аналитического выражения построить таблицу истинности. Представить функцию в форме СДНФ, упростить полученную СДНФ функции, построить таблицу истинности для упрощенного выражения. Сравнить полученные результаты.

Заданная функция .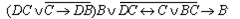

Основные теоретические положения.

Для работы со сложными формулами в Excel реализован Мастер функций, хотя формулу можно вводить и непосредственно с клавиатуры. При конструировании формулы с помощью Мастера функций в диалоговом окне отображается имя функции, все ее аргументы, описание функции и каждого аргумента, текущий результат функции и всей формулы.

Функции и выражения могут быть вложены друг в друга, что позволяет конструировать проверку достаточно сложных условий.

В Excel имеются следующие логические функции: ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ.

Описание каждой функции можно найти в Мастере функций.

Экспериментальные результаты.

Построение таблицы истинности заданной функции.

Таблица строится с использованием логических функций.

B, C ,D – столбцы аргументов функции.

Для упрощения построения таблицы и визуального восприятия ввел дополнительные переменные. Значения переменных показаны в таблице1.

⌐(C→DB)	H
DC↔C˅BC	G

Таблица 1 – Значение промежуточных переменных.

B	C	D	DC	DB	H	DC˅H	⌐G	(DC˅H)B˅⌐G	F

Таблица2 – Таблица истинности, с промежуточными результатами.

Столбец DCреализует функцию И, используя в качестве аргументов ячейки столбцов Dи C. Для строки4 формула выглядит следующим образомf(x)=И(D4;C4).

Столбец DBреализует функцию И, используя в качестве аргументов ячейки столбцов D иB. Для строки 4 формула выглядит следующим образомf(x)=И(D4;C4).

Столбец Hсодержитзначение⌐(C→DB), как показано в таблице 1. И реализует функцию инверсии, импликации аргументов ячеек столбцовCи DB.Функции импликации нет в списке логических функций, реализуемых в Excel, поэтому эту функцию реализовал с использованием функции ЕСЛИ.Для строки 4 формула выглядит следующим образом f(x)=НЕ(ЕСЛИ(И(C4=1;F4=ЛОЖЬ);ЛОЖЬ;ИСТИНА)).

Столбец DC˅H реализует функцию ИЛИ, используя в качестве аргументов ячейки столбцов DCи H. Для строки 4 формула выглядит следующим образом f(x)=ИЛИ(E4;G4).

Столбец ⌐G содержит инверсию значения DC↔C˅BC, как показано в таблице 1.Реализует функцию инверсии, эквивалентности столбца аргументов DC и результата функции И столбцов аргументов С и ВС.Функции эквивалентности также нет в списке логических функций, реализуемых в Excel, поэтому эту функцию необходимо реализовать с использованием функции ЕСЛИ. Для 4 строки формула выглядит следующим образом f(x)=НЕ(ЕСЛИ(И(D4;C4)=ИЛИ(C4;И(B4;C4));ИСТИНА;ЛОЖЬ)).

Столбец (DC˅H)B˅⌐G реализует функцию И, использую значения аргументов ячейки столбцов DC˅H и B. Также, по полученному результату, реализует функцию ИЛИ, используя в качестве аргументов полученный результат предыдущей функции и значенияаргументов ячеек столбца B.

Последний столбец таблицы F соответствует реализации функции импликации, используя в качестве аргументов ячейки столбцов (DC˅H)B˅⌐G и В. Для строки 4 формула выглядит следующим образом f(x)=ЕСЛИ(И(J4=ИСТИНА;B3=0);ЛОЖЬ;ИСТИНА)

Дополнительно результат может быть представлен в более удобной для анализа форме с использованием двоичного алфавита (дополнительный столбец F) с использованием формулы f(x)=ЕСЛИ(K4=ИСТИНА;1;0).

Результат построения таблицы истинности показан на рисунке 1.

Рисунок 1 – Таблица истинности функции