Определить диапазон частот, в котором рассматриваемое поле представляет собой волну, бегущую вдоль оси z

Основные уравнения электродинамики

Тема 1

Выполнил студент группы СС.1003 ОТФ-2 _______________ С.Э. Нистратов

Москва 2012

Задача № 1-23

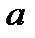
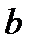
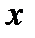
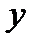
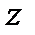В соответствии с заданием исследовать основные свойства монохроматического электромагнитного поля существующего прямоугольном волноводе. Волновод заполнен однородной изотропной средой с параметрами 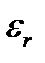, , 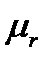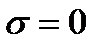. Стенки волновода являются идеально проводящими. Известны выражения для составляющих векторов поля.

;

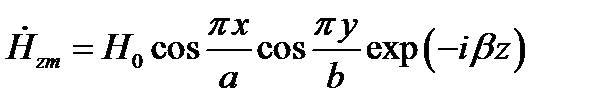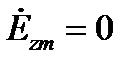
Требуется:

1. Используя уравнения Максвелла, найти комплексные амплитуды всех остальных заданных в условии задачи, составляющих векторов 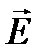и .

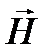2. Определить диапазон частот, в котором рассматриваемое поле представляет собой волну, бегущую вдоль оси z.

3. Записать выражения для мгновенных значений всех составляющих векторов поля. Рассчитать и построить графики зависимостей мгновенных значений составляющих от координаты z (при x=a/3, y=b/3) в два момента времени: t₁=0 и t₂=T/4 в интервале 0≤ z ≤2Λ, где Λ-длина волны в волноводе на частоте f₂.

4. Проверить выполнение граничных условий на стенках волновода (при x=0;a и y=0;b)

5. Определить максимальные значения плотностей продольного и поперечного поверхностных токов на всех стенках волновода на частоте f₂.

6. Вычислить средний за период поток энергии через поперечное сечение волновода на частоте f₂.

7. Определить фазовую скорость V_Ф и скорость распространения энергии волны V_Э на частоте f₂. Рассчитать и построить графики зависимостей этих скоростей от частоты.

8. Нарисовать структуру векторных линий полей и эпюры токов на стенках волновода.

Исходные данные:

H₀= 0 A/м

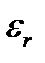=4

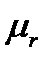=1

a= 60 мм

b=20 мм

f₁=2.5 ГГц

f₂=5 ГГц

1. Используя уравнения Максвелла, найти комплексные амплитуды всех остальных заданных в условии задачи, составляющих векторов 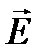и .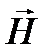

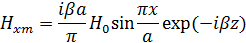
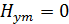
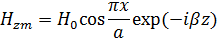
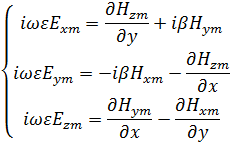
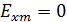
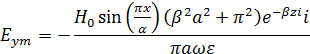
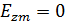
Определить диапазон частот, в котором рассматриваемое поле представляет собой волну, бегущую вдоль оси z.

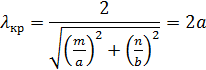
a= 50 мм =0,05 м ; b= 30 мм = 0,03 м

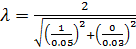=0.1

Из выражения 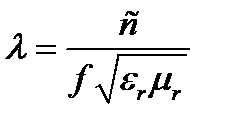можно определить критическую частоту: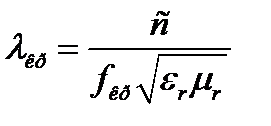

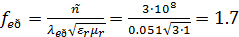ГГц

Условие распространения волны: 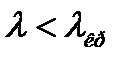или 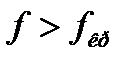т.е. волна будет распространятся в диапазоне частот от 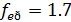ГГц до бесконечности. В этом диапазоне 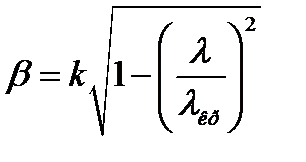остается вещественной.

3. Записать выражения для мгновенных значений всех составляющих векторов поля. Рассчитать и построить графики зависимостей мгновенных значений составляющих от координаты z (при x=a/3, y=b/3) в два момента времени: t₁=0 и t₂=T/4 в интервале 0≤ z ≤2Λ, где Λ-длина волны в волноводе на частоте f₂.

На разных частотах коэффициент β будет вещественным или комплексным.

На частоте f1=0,5 ГГц коэффициент β – комплексный, т.к. эта частота не попадает в диапазон частот, при которой волна распространяется. β= -ja

Мгновенные значения составляющих вектора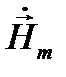

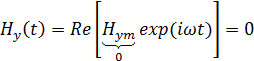
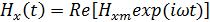
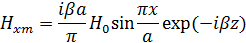
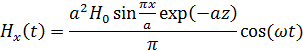
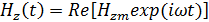
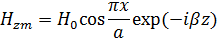
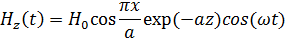
Мгновенные значения составляющих вектора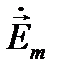

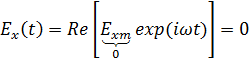
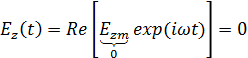
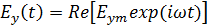
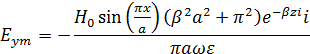
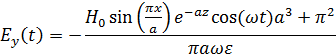
На частоте f2=4 ГГц, которая входит в диапазон частот, на которой волна распространяется, β следует принимать за вещественное число.

Мгновенные значения составляющих вектора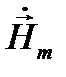

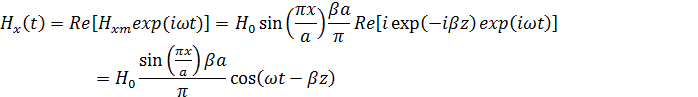
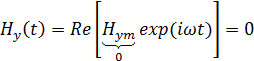
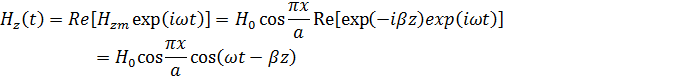
Мгновенные значения составляющих вектора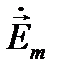

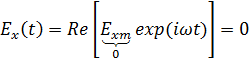
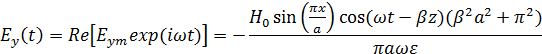
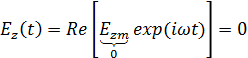
Длина волны в волноводе равна 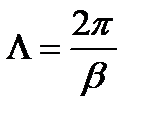, где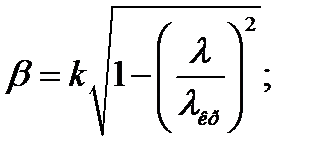

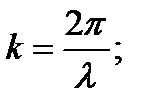
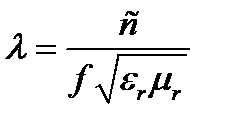
На частоте f1

При t2 При t1 Нx, А/м

Нz, А/м При t2 При t1

При t1 При t2 Ey, В/м

На частоте f2

При t2 При t1 Нx, А/м

При t1 При t2 НZ, А/м

Ey, В/м При t2 При t1 При t2 При t1 Ey, В/м

4. Проверить выполнение граничных условий на стенках волновода (при x=0;a и y=0;b)

x

y

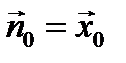
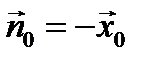
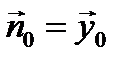
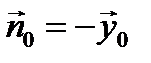
На боковых стенках волновода (x=0,a)

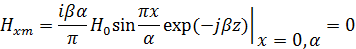
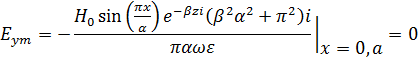
На верхней и нижней стенках волновода (y=0,b)

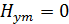
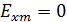
Граничные условия выполняются на всех стенках волновода.

5. Определить максимальные значения плотностей продольного и поперечного поверхностных токов на всех стенках волновода на частоте f₂.

Плотности тока на стенках волновода определяются следующим выражением.

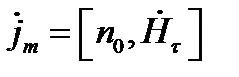
Плотности тока на правой боковой стенке волновода (x=0).

Продольный ток

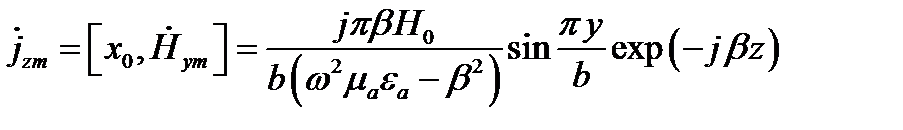
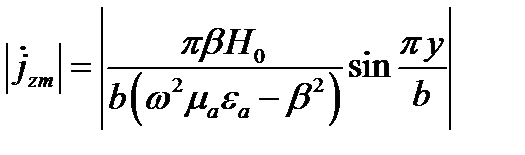
Максимум этого тока при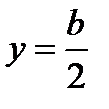

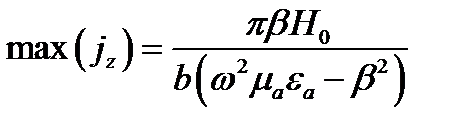
Поперечный ток

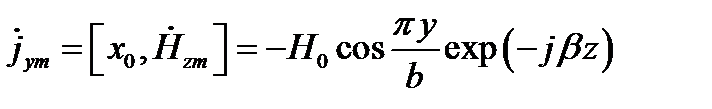
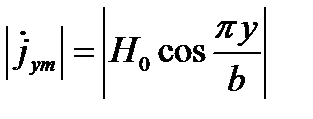
Максимум этого тока при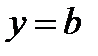

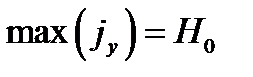
Плотности тока на левой боковой стенке волновода (x=а).

Продольный ток

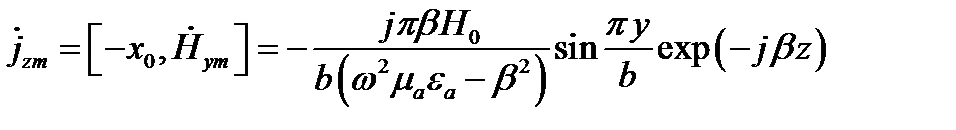
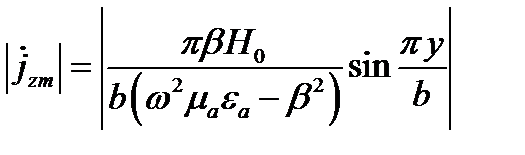
Максимум этого тока при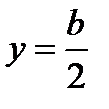

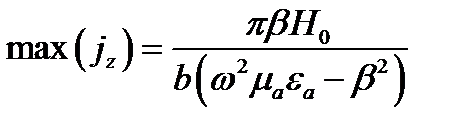
Поперечный ток

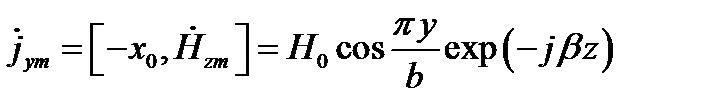
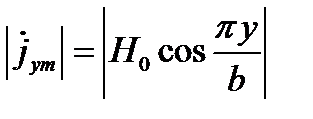
Максимум этого тока при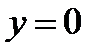

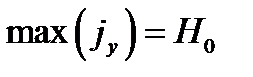
Плотности тока на нижней стенке волновода (y=0)

Продольный ток

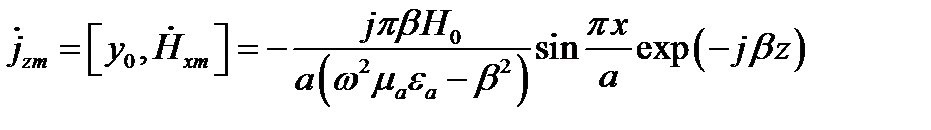
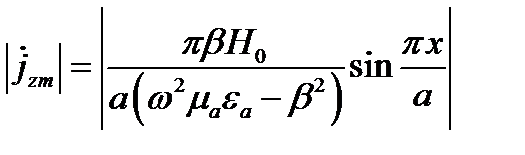
Максимум тока будет при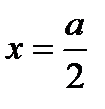

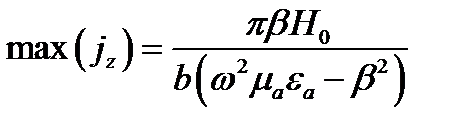
Поперечный ток

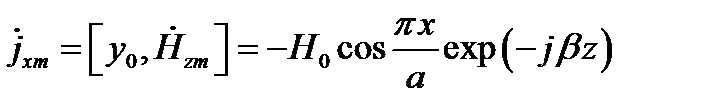
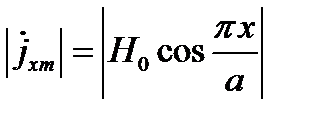
Максимум тока будет при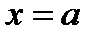

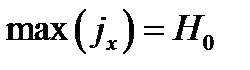
Плотности тока на верхней стенке волновода (y=b)

Продольный ток

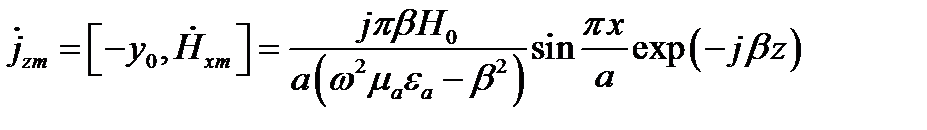
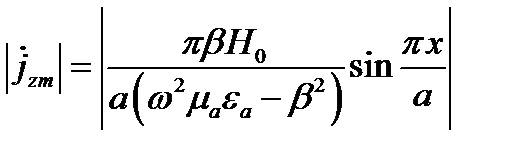
Максимум тока будет при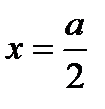

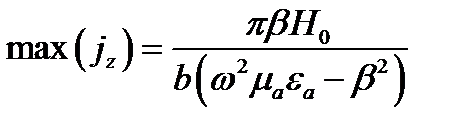
Поперечный ток

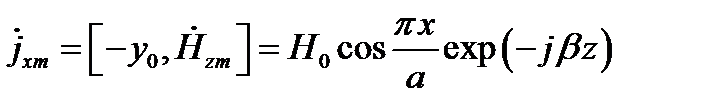
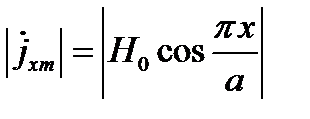
Максимум тока будет при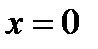

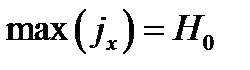
Продольные токи Поперечные токи

6. Вычислить средний за период поток энергии через поперечное сечение волновода на частоте f₂.

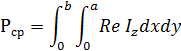
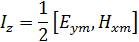
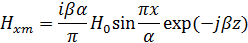
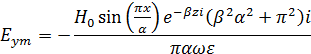
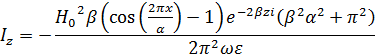
На частоте f2 β следует принимать за вещественное число.

Re[ ]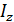

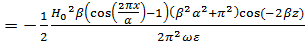
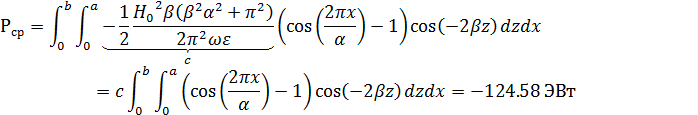
7. Определить фазовую скорость V_Ф и скорость распространения энергии волны V_Э на частоте f₂. Рассчитать и построить графики зависимостей этих скоростей от частоты.

Фазовая скорость определяется по следующей формуле

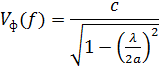
На частоте f₂ фазовая скорость будет равна

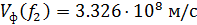
Скорость энергии можно определить по следующей формуле

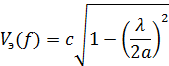
На частоте f₂ скорость распространения энергии равна

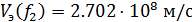
Графики скоростей

V, м/с VЭ VФ