Перевод правильных дробей
Системы счисления, используемые в вычислительной технике
Для выполнения арифметических действий в позиционных системах счисления используются одинаковые правила и таблицы сложения, вычитания, умножения. Можно обойтись без таблиц, если хорошо знать эти правила для десятичной системы счисления и в процессе вычисления всегда помнить, что есть число 10 в данной системе счисления.
В дальнейшем числа в системе счисления с основанием Р будем помечать (p), в десятичной — без индекса.
В очевидных случаях индекс будем опускать. Базовые значения цифр будем записывать в десятичной системе счисления.
Современные вычислительные машины на аппаратном уровне работают в двоичной системе счисления, т.е. они оперируют с двумя числами: 0 и 1. Но числа, записанные в виде 10011101001000110,трудно воспринимаются человеком. Мы привыкли работать в десятичной системе.
Для решения этой проблемы возможно либо представлять базовые цифры десятичной системы в двоичной форме (так называемая двоично-десятичная система), либо разработать алгоритмы перевода десятичных чисел в двоичные.
В вычислительной технике широко используются:
· двоичная система (основание= 2), базисные цифры:
0 и 1;
· восьмеричная (основание= 8), базисные цифры:
0 1 2 3 4 5 6 7;
· десятичная (основание= 10), базисные цифры:
0 1 2 3 4 5 6 7 8 9;
· шестнадцатеричная (основание= 16), базисные цифры:
0 1 2 3 4 5 6 7 8 9 A B C D E F.
Особое положение занимает смешанная двоично-десятичная система, в которой каждая десятичная цифра заменяется четырьмя двоичными разрядами:
24(10) = 0010 0100(2-10).
7485(10) = 0111 0100 1000 0101(2-10).
1001001001010000111(2-10)= 0100 1001 0010 1000 0111(2-10)= 49287(10).
Перевод чисел из одной системы счисления в другую
Под задачей перевода понимается задача нахождения цифр числа Х, заданного в системе счисления с основанием P, в системе счисления с основанием Q.
Перевод чисел из одной системы в другую основан на том, что значение числа не зависит от формы его представления. Число пять пальцев можно записать по разному, но количество пальцев останется равным пяти.
Пусть есть одна система с основанием Р, а другая с основанием Q. Число Хможно представить по формуле полинома (2.2):
X=Am ×Pm +A m-1×Pm-1 +...+A 1×P1+A0 ×P 0+A-1 ×P-1 +...A-n ×P-n , (2.4)
Х=Bk ×Qk +B k-1×Qk-1 +...+B 1×Q1+B0 ×Q 0 +B-1 ×Q-1 +...B-j ×Q-j. (2.5)
Итак, мы имеем два уравнения со многими неизвестными, т.е. они не имеют аналитического решения.
Однако если мы знаем, как представить каждую базисную цифру системы Р в системе Q и умеем пользоваться арифметикой системы Q, то вычислить значение числа не сложно по формуле (2.4).
Перевод чисел из произвольной системы в десятичную
Удобно переводить числа из произвольной системы в десятичную по формуле полинома (2.4).
В этом случае используется разложение числа Х по степеням основания, в котором базовые значения цифр и степени основания представляют в десятичной системе и выполняют все действия в этой же системе.
Пример.
1. Перевести число 11001.1(2) из двоичной системы в десятичную.
11001.1(2)=1×24 +1×23 +0×22 +0×21 +1×20 +1×2-1 =16+8+1+1/2=25.5(10).
2. Перевести число 123(8) из восьмеричной системы в десятичную.
123(8)= 1×82 +2×81+30 =64+16+3=83(10).
3. Перевести число 20А.0С(2) из двоичной системы в десятичную.
20A.0C(16)=2×162 +0×161 +A×160 +0×16-1 +C×16-2 =
=2×256+0×16+10×1+0×1/16+12×1/256=522.046875(10).
Перевод чисел из десятичной системы в произвольную
При переводе из десятичной системы в произвольную можно воспользоваться полиномом (2.4), но нужно пользоваться арифметикой той системы, из которой мы переводим число. А это затруднительно, т.к. мы, как правило, не знаем не только таблицы умножения в системах, отличных от десятичной, но и таблицу сложения и вычитания!
Целые числа и правильные дроби переводятся по разным правилам.
Перевод целых чисел
Пусть задано Х — целое число в системе P. Требуется найти цифры этого числа в системе счисления с основанием (10).
Алгоритм перевода целых чисел основан на делении целого числа на основание системы:
1. Исходное число X=Am ×Pm +A m-1×Pm-1 +...+A 1×P1+A0 ×P 0 делим на основание Р:
X/P= Am ×Pm-1 +A m-1×Pm-2 +...+A 1×P0+ A0 /P.
2. Разделяем результат на целую и дробную части:
Целая [X/P]= Am ×Pm-1 +A m-1×Pm-2 +...+A 1×P0.
Дробная {X/P}= A0 /P.
Т.к. любая базовая цифра меньше основания системы, то A0/P >=0.
3. Находим А0:
А0= {X/P}× P= остатку от деления.
4. Целую часть снова делим на основание и получаем A1:
[X/P]/P= Am ×Pm-2 +A m-1×Pm-3 +...+A0+A 1×P-1.
5. Повторяем п.4, пока целая часть не станет равной 0.
На каждой итерации остаток от деления представляет собой коэффициент полинома Ai.
6. Записываем остатки и последнее частное в порядке, ОБРАТНОМ их получению в НОВОЙ системе счисления.
Пример.
1. Перевести число 13 из десятичной системы в двоичную.
13/2= 6, остаток 1 ® A0;
6/2= 3, остаток 0 ® A1;
3/2= 1, остаток 1 ® A2;
1/ 2=0, остаток 1 ® A3.
Запишем результат:
13(10)=1101(2).
2. Перевести число 13 из десятичной системы в восьмеричную.
13/8= 1, остаток 5 ® A0;
1/8= 0, остаток 1 ® A1.
Запишем результат:
13(10)= 15(8).
3. Перевести число 13 из десятичной системы в шестнадцатеричную
13/16= 0, остаток 13 ® A0.
Запишем результат:
13(10)= 13(16).
Особый случай возникает, если между основаниями систем существует соотношение:
P= Qn . (2.6)
В этом случае каждую базисную цифру системы Р можно представить n-разрядным числом в системе Q.
Для двоичной и восьмеричной системы справедливо:
23 =8.
Каждой восьмеричной цифре соответствует двоичный код из 3-х цифр. Такой код называется ТРИАДОЙ. Запишем триады всех восьмеричных цифр:
0 – 000, 4 – 100,
1 – 001, 5 – 101,
2 – 010, 6 – 110,
3 – 011, 7 – 111.
Пример.
1. Перевести число 13 из восьмеричной системы в двоичную.
13(8)= 001 011(2).
2. Перевести число 10100101100101 из двоичной системы в восьмеричную.
10 100 101 100 101(2)= 24545(8).
3. Перевести число 13 шестнадцатеричной системы в двоичную.
13(16)= 0001 0011(2).
4. Перевести число 10100101100101 из двоичной системы в шестнадцатеричную.
10 1001 0110 0101(2)= 2965(16).
Перевод правильных дробей
Пусть X(p) — правильная дробь в системе счисления с основанием P=10. Требуется найти цифры этого числа в системе счисления с основанием Q.
Воспользуемся полиномом (2.4), но будем использовать только дробную часть.
Х=0 ×Q 0 +B-1 ×Q-1 +B-2 ×Q-2 +...B-j ×Q-j.
Значение X представляет собой дробную часть, т.е. X= {X}.
Умножим Х на основание системы Q:
Х×Q=0 ×Q 1 +B-1 × Q0 +B-2 ×Q-1 +...B-j ×Q-j+1 =[X]+ {X} .
Подчеркнутая часть представляет собой целое число (возможно 0), т.к. все базисные числа целые, а Q0= 1. Следовательно, целая часть, полученная после умножения, есть первая цифра искомого числа. Далее выделяем дробную часть и снова умножаем ее на основание системы.
Процесс умножения заканчивается в двух случаях:
1) когда на каком-то шаге получится дробная часть, равная 0. В этом случае дробь переводится в новую систему ТОЧНО;
2) дроби в новой системе счисления соответствует БЕСКОНЕЧНАЯ дробь. В этом случае процесс заканчивают получением наперед заданного случае количества цифр. Часто выделяется период бесконечной дроби.
Пример.
1. Перевести число 0.25 из десятичной системы в двоичную.
0.25 0.50
´ 2 ´ 2
0.50 1.00

0. 0 1, т.е. число 0.25(10)= 0.01(2).
2. Перевести число 0.25 из десятичной системы в восьмеричную.
0.25
´ 8
2.0

0.2, т.е. число 0.25(10)= 0.2(8)
3. Перевести число 0.3 из десятичной системы в шестнадцатеричную.
0.3 0.8 0.8
´ 16 ´ 16 ´16
4.8 12.8 12.8


0. 4 С С ….., т.е. число 0.3(10)= 0.ССС…..(16)
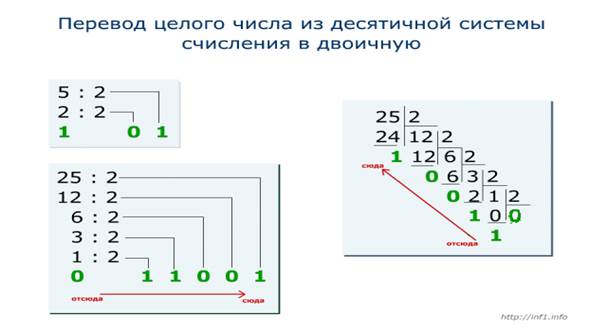
Перевод целого числа из десятичной системы счисления в двоичную осуществляется по следующей схеме: десятичное число делится нацело на основание 2, затем на 2 делятся последовательно все частные от целочисленного деления, до тех пор пока частное не станет меньше основания. В результат заносится последнее частное и все остатки от деления, начиная с последнего.
