Сравнение методов Гаусса с частичным и полным выбором главного элемента по точности и вычислительной сложности

В предыдущей лекции было установлено, что для решения СЛАУ методом Гаусса очень важное значение имеют величины главных элементов: чем меньше модуль главного элемента, тем больше погрешность получаемого решения СЛАУ, поскольку деление на малый по модулю элемент приводит к значительному увеличению коэффициентов соответствующего уравнения. При полном выборе главного элемента область матрицы СЛАУ, используемая для этого выбора, значительно шире, чем при частичном. Это приводит к тому, что при полном выборе главного элемента модуль его значения на 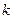-ом шаге прямого хода метода Гаусса всегда не меньше, чем при частичном выборе на том же 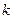-ом шаге, значит погрешность решения СЛАУ методом Гаусса с полным выбором главного элемента всегда не больше, чем при использовании метода Гаусса с частичным выбором. Наименее точным является метод Гаусса без выбора главного элемента. Таким образом, если расположить варианты метода Гаусса в порядке уменьшения точности получаемого ими решения СЛАУ, то этот порядок будет следующий:

1. Метод Гаусса с полным выбором главного элемента;

2. Метод Гаусса с частичным выбором главного элемента;

3. Метод Гаусса без выбора главного элемента.

Методы Гаусса с частичным и полным выбором главного элемента отличаются друг от друга только в способе выбора главного элемента. Процессы пересчета элементов матрицы СЛАУ и вектора правой части в ходе исключения, а также обратный ход у этих двух методов абсолютно одинаковы. Поэтому все отличия, которые возникают у этих двух методов обязаны лишь отличиям в главных элементах.

Вычислительная сложность методов Гаусса с частичным и полным выбором главного элемента определяется в соответствии с формулами (30) и (40) и равна 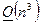для СЛАУ размером 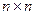, но несмотря на то, что в обоих методах общее количество операций определяется как многочлен третьей степени от размера СЛАУ, в силу соотношений (15) и (35) становится очевидно, что прямой ход метода Гаусса с полным выбором главного элемента (а значит и метод Гаусса с полным выбором главного элемента в целом) требует бóльшего количества операций (за счет операций сравнения), чем прямой ход метода Гаусса с частичным выбором главного элемента (а значит и метод Гаусса с частичным выбором главного элемента в целом). Заметим, что если выбор главного элемента вообще не производится, то операции сравнения здесь будут отсутствовать, но пересчет элементов матрицы СЛАУ и вектора правой части будет осуществляться также, как и в методах Гаусса с выбором главного элемента и потребует для этого снова 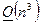арифметических операций, т.е. вычислительная сложность метода Гаусса без выбора главного элемента также составляет .

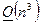Если схематически изобразить графики зависимости количества операций от размера системы при решении СЛАУ различными вариантами метода Гаусса, то качественно это будет выглядеть так, как показано на рис.3. Все графики – части кубических парабол, но с различной скоростью роста. Очень хорошо видно (рис.3), что для фиксированной СЛАУ (размера 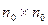) меньше всего потребуется операций для ее решения методом Гаусса без перестановок, а больше всего – методом Гаусса с полным выбором главного элемента.

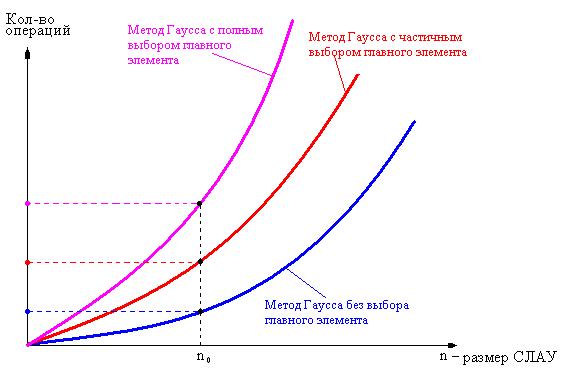
Рис.3.