Машинное представление вещественных чисел. Арифметика с плавающей точкой

Элементы теории погрешностей.

Определение №1. Значащей цифрой числа называется любая цифра в его десятичном изображении, начиная с первой ненулевой слева.

Определение №2. Пусть 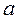– некоторая неизвестная точная величина, 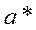- известное ее приближенное значение. Тогда абсолютная погрешность 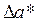определяется из неравенства:

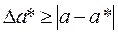
Определение №3.Относительная погрешность 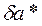определяется из неравенства:

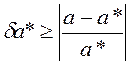
Замечание №1

1. Точность числа лучше характеризует относительная погрешность, выраженная в процентах.

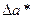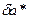2. В записи и больше двух значащих цифр, как правило, не берут.

Определение №4.Значащая цифра числа называется верной, если абсолютная погрешность не превосходит половины разряда, в котором стоит данная цифра.

Определение №5.Не верные значащие цифры называются сомнительными.

Замечание №2

1. Если все цифры числа – верные, то это не точное число, но имеющее вполне определенную погрешность.

2. Если приближенное число имеет все верные значащие цифры, то его округленное число также имеет все верные значащие цифры.

Правила округления чисел.

Для округления числа до 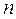значащих цифр следует отбросить все его цифры, стоящие справа от 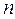– ой значащей цифры. При этом:

1. Если первая из отброшенных значащих цифр меньше 5, то оставшиеся десятичные знаки сохраняются без изменения.

2. Если первая из отброшенных цифр больше 5, либо равна 5 и среди остальных отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляется единица.

3. Если первая из отброшенных цифр равна 5 и остальные отброшенные цифры нулевые, то последняя оставшаяся цифра не изменяется, если она четная и увеличивается на единицу, если она нечетная.

Пример №1. Округлить число 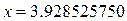до 7, 6, 5,4, 3, 2, 1 десятичного знака и до единиц:

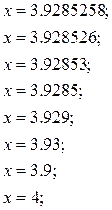
Определение №6. Прямая задача теории погрешностей состоит в указании погрешности функций по известным погрешностям их аргументов:

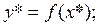
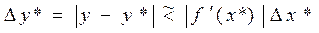
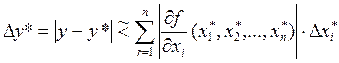
Определение №7. Обратная задача теории погрешностей состоит в указании допустимой погрешности аргументов по известной погрешности функции.

В случае функции от одной переменной задача имеет единственное решение и только в этом случае:

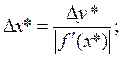
где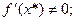

В случае 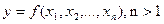задача будет иметь единственное решение лишь при следующих предположениях:

1. Все аргументы функции одинаково влияют на ее погрешность, т. е.

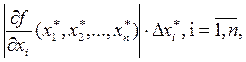
равны друг другу (принцип равных влияний). Тогда

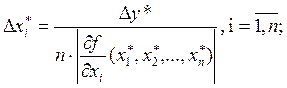
2. 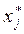- более всего определяет погрешность:

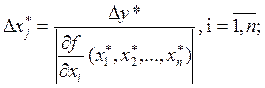
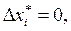
при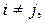

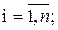
Машинное представление вещественных чисел. Арифметика с плавающей точкой.

Определение №1. Десятичное число с плавающей точкой – это число представленное в ви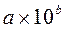де , где 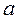- мантисса, а 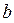- показатель (порядок).

Обычно, число 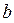- целое, а у числа 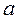слева от десятичной точки находится только один знак. У обоих чисел 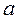и 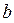количество разрядов конечно, поэтому имеется конечное множество чисел с плавающей точкой, и, в частности существуют наибольшее и наименьшее числа с плавающей точкой. Чтобы избежать неоднозначности обычно требуют, чтобы первая цифра мантиссы 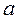была ненулевой (нормализация). В компьютере с двоичной арифметикой числа с плавающей точкой представляются 32, либо 48, либо 64 двоичными разрядами – битами. Стандарт IEEE отводит 24 бита для мантиссы и 8 битов для показателя в 32 разрядном компьютере (40 и 8 для 48 – разрядного, 53 и 11 для 64 - разрядного компьютера). Предполагается, что самый левый бит мантиссы любого числа равен единице, что позволяет его не хранить. По техническим причинам в 32 – разрядном компьютере показатель хранится как целое число в интервале [ 0 , 255 ], чтобы получить фактическое значение показателя, нужно вычесть 127 из хранимого числа. Значение 255 резервируется для представления бесконечности, а также для указания незаконных результатов, например, извлечение корня квадратного из отрицательного числа. Подобные незаконные результаты называют «не числами».

Машинные константы

В 32 – разрядном компьютере существует наибольшее число с плавающей точкой:

;

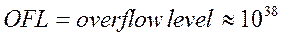а также наименьшее число с плавающей точкой:

;

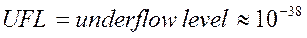Определение №2. Наименьшее число с плавающей точкой, которое при сложении с числом 1.0 дает результат больший, чем 1.0, называется машинным .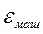

Конкретное значение 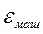зависит от того, какая арифметика используется – с округлением или с усечением.Дело в том, что арифметические операции над числами с плавающей точкой не всегда приводят к точным результатам, поэтому результат приходиться округлять или усекать до ближайшего числа с плавающей точкой.

Для 32 – битовой арифметики с плавающей точкой, удовлетворяющей стандарту IEEE, 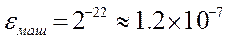, при использовании округлений. Это значит, что всякое десятичное число меньшее 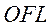и большее 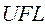может быть представлено с шестью – семью десятичными знаками точности. 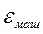определяет относительную погрешность арифметики компьютера. Если 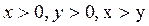, то их сумму можно записать в виде:

.

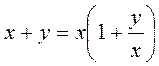Очевидно, что при ,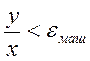

.

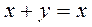Более тщательное исследование показывает, что относительная погрешность сложения ограничена величиной .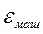

Запись десятичного числа, скажем 0.7, в память компьютера сопряжена с ошибкой, поскольку 0.7 не имеет точного двоичного представления. Как правило, ошибки представления локализованы в последнем бите:

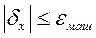
Это означает, что относительная погрешность хранимого приближения с плавающей точкой числа 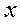может достигать величины .

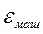Числа с плавающей точкой между 0 и 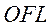распределены неравномерно. Между каждыми двумя соседними степенями двойки находится 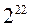чисел с плавающей точкой, например, 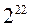чисел между 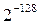и 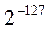, столько же чисел между 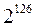и 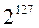. Таким образом, числа с плавающей точкой гуще расположены вблизи нуля.

Константы 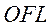и 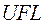определяются, главным образом, количеством битов показателя, тогда как 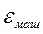– количеством битов мантиссы. Имеет место неравенство: