При моделировании аналогового сигнала на ЭВМ следует принять

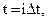
где 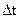- временной интервал между двумя соседними расчетными точками, i – порядковый номер расчетной точки, изменяющийся от 0 до i_max.

Значения X₁, X₂, X₃, φ₁, φ_2, φ₃, F₁ и Δt приведены в таблице 1.

Таблица 1. Исходные данные для выполнения задания №1

Номер варианта- -последняя цифра номера студенческого билета	X1	X2	X3	φ1	φ 2	φ 3	F1	FД	Δt
			0.5				1кГц	8кГц	1/512 мс

2. Определить амплитудный спектр аналогового сигнала.

3. Сформировать вспомогательный сигнал 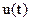в виде периодической последовательности единичных отсчетов с периодом, равным интервалу дискретизации 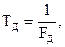где

F_Д – частота дискретизации . Значение F_Д приведено в таблице 1.

4. Сформировать дискретный сигнал .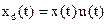

5. Определить амплитудные спектры аналогового и дискретного сигналов и убедиться в том, что при дискретизации имеет место эффект размножения спектра аналогового сигнала.

6. Восстановить аналоговый сигнал из дискретного путем выделения из спектра дискретного сигнала той части, которая соответствует спектру аналогового сигнала. Сравнить восстановленный сигнал с исходным аналоговым сигналом.

7. Повторить машинный эксперимент при в два раза меньшей частоте дискретизации. Убедиться в том, что восстановленный сигнал отличается от исходного аналогового сигнала, и объяснить причину искажения восстановленного сигнала.

Расчет частот спектральных составляющих дискретного сигнала по формуле

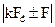
k = 0

1. F=F₁, f₁ = F₁ = 1 КГц,

2. F=F₂, f₂ = F₂ = 2 КГц,

3. F=F₃, f₃ = F₃ = 3 КГц.

K=1

4. F=F₃, f₄ = F_d – F₃ = 8 – 3 = 5 КГц,

5. F=F₂, f₅ = F_d – F₂ = 8 – 2 = 6 КГц,

6. F=F₁, f₆ = F_d – F₁ = 8 – 1 = 7 КГц,

7. F=F₁, f₇ = F_d + F₁ = 8 + 1 = 9 КГц,

8. F=F₂, f₈ = F_d + F₂ = 8 + 2 = 10 КГц,

9. F=F₃, f₉ = F_d + F₃ = 8 + 3 = 11 КГц.

Построение спектральных диаграмм аналогового и дискретного сигналов

Рисунок 1 – Амплитудный спектр аналогового сигнала

Рисунок 2 – Амплитудный спектр дискретного сигнала

На рисунке 2 амплитудный спектр представлен в относительном масштабе по оси ординат как отношение амплитуды спектральной составляющей X к максимальной амплитуде X_max.

1. Результат моделирования по программе «Diskret» при исходных данных таблицы 1 в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 3

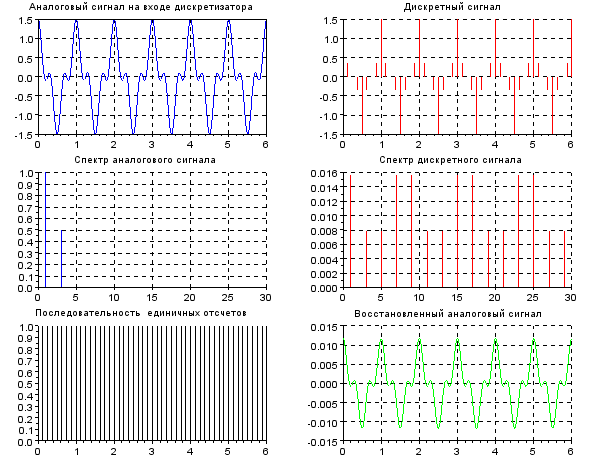Рис. 3 Временные и спектральные диаграммы при F_Д > 2F₃

Выводы:

§ Сгустки спектра дискретного сигнала размножаются относительно сатоты дискретизации.

§ Восстановленный аналоговый сигнал схож с начальный аналоговым сигналом. Из чего можно сделать вывод о том, что при выбранной частоте дискретизации, большей в 2 раза частоты сигнала- теорема Котельникова работает.

2. Повторим эксперимент при меньшей в два раза частоте дискретизации.

Результат моделирования в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 4.

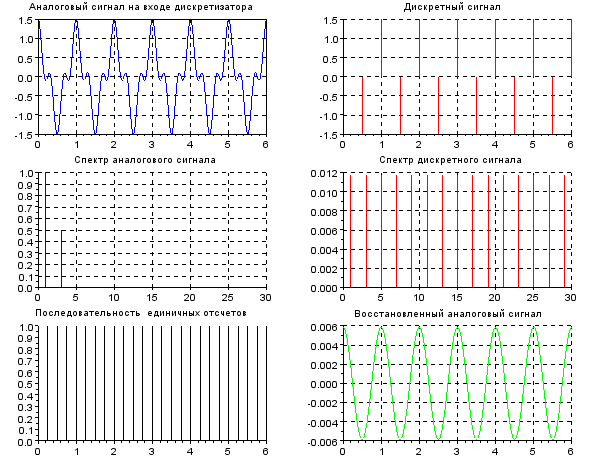
Рисунок 4. Временные и спектральные диаграммы при F_Д < 2F₃

· Из рисунка видно, что при меньшей частоте дискретизации спектральные сгустки накладываются друг на друга

· Восстановленный аналоговый сигнал не соответствует заданному аналоговому сигналу. Из этого делаем вывод о том, что теорема Котельникова не работает, в случае, с выбранной в 2 раза меньшей частотой дискретизации.

Приложение А

Моделирование процесса дискретизации аналогового сигнала

и восстановления аналогового сигнала из дискретного

// Программа "Diskret". Моделирование процесса дискретизации// аналогового сигнала и восстановления аналогового сигнала// из дискретного//// Ввод исходных данных для моделирования//X1=1; //Амплитуда первой гармоникиX2=0; //Амплитуда второй гармоникиX3=0.5; //Амплитуда третьей гармоникиphi1=0; //Начальная фаза первой гармоникиphi2=0; //Начальная фаза второй гармоникиphi3=0; //Начальная фаза третьей гармоникиF1=1 // Частота первой гармоники сигналаFd=4 // Частота дискретизацииdelta_t=1/512; //Временной интервал между двумя соседними //расчетными точками//// Расчет вспомогательных параметровis=ceil(1/(F1*delta_t)); //Количество расчетных точек в периоде сигналаid=ceil(1/(Fd*delta_t)); //Количество расчетных точек в интервале // дискретизацииimax=64*is; // Количество расчетных точекI=6*is; // Количество расчетных точек на графике////Начальная установка (обнуление массивов)i=zeros(1:imax);x=zeros(1:imax);u=zeros(1:imax);xd=zeros(1:imax);xv=zeros(1:imax);s=zeros(1:imax);sd=zeros(1:imax);sv=zeros(1:imax);i0=zeros(1:I);x0=zeros(1:I);u0=zeros(1:I);xd0=zeros(1:I);xv0=zeros(1:I);t=zeros(1:I);u=zeros(1:imax)z=0//// Формирование аналогового сигнала//for i=1:imax x1=X1*cos(2*%pi*F1*delta_t*i+phi1); x2=X2*cos(4*%pi*F1*delta_t*i+phi2); x3=X3*cos(6*%pi*F1*delta_t*i+phi3); x(i)=x1+x2+x3;//// Формирование последовательности единичных отсчетов// z=z+1 if z = = id then z=0 end if z= = 0 then u(i)=1 else u(i)=0 end//// Дискретизация аналогового сигналаxd(i)=x(i)*u(i);end// Формирование массивов данных для построения графиковfor i0=1:I x0(i0)=x(i0); u0(i0)=u(i0); xd0(i0)=xd(i0); endi0=[1:I];t=delta_t*i0;clf()// Очистка графического окна перед выдачей графиковsubplot(3,2,1);xtitle('Аналоговый сигнал на входе дискретизатора')plot(t,x0,"b")xgridsubplot(3,2,5);xtitle('Последовательность единичных отсчетов')plot2d3(t,u0)subplot(3,2,2);xtitle('Дискретный сигнал')plot2d3(t,xd0,style=[color("red")])xgrid////Определение спектра аналогового и дискретного сигнала//s=fft(x);sd=fft(xd);kmax=30*floor(imax/is);k=zeros(1:kmax);f=zeros(1:kmax);s0=zeros(1:kmax);sd0=zeros(1:kmax);k=[1:kmax];f=k/(delta_t*imax);for k=1:kmax s0(k)=s(k)*2/imax; sd0(k)=sd(k)*2/imax; endsubplot(3,2,3)xtitle('Спектр аналогового сигнала')plot2d3(f,abs(s0),style=[color("blue")])xgridsubplot(3,2,4)xtitle('Спектр дискретного сигнала')plot2d3(f,abs(sd0),style=[color("red")])xgrid//// Восстановление аналогового сигнала из дискретного//k1=floor(0.5*imax/id);// Номер отсчета спектра,// соответствующий половине частоты дискретизацииfor k=1:imax if k<k1 then sv(k)=sd(k);else sv(k)=0; endend// Формирование восстановленного сигналаxv=ifft(sv);for i0=1:I xv0(i0)=xv(i0); endsubplot(3,2,6)xtitle('Восстановленный аналоговый сигнал')plot2d(t,xv0,style=[color("green")])xgrid

Задание №2.Определение системной функции, комплексного

коэффициента передачи, АЧХ и ФЧХ цифрового фильтра

Требуется определить системную функцию H(z), комплексный коэффициент передачи K(jθ), АЧХ K(f_N) и ФЧХ φ(f_N) цифрового фильтра, где θ = 2π f_N, f_N=f/F_Д – нормированная частота. Построить графики АЧХ и ФЧХ

В таблице 2 приведены коэффициенты системной функции фильтра.

Таблица 2. Алгоритм функционирования и параметры цифрового фильтра

Номер варианта	Номер рисунка	Коэффициенты системной функции фильтра
		B0 = B2 = 0.65, B1 = 1

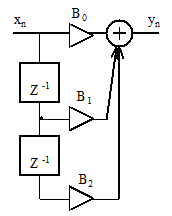
Требуется определить системную функцию 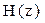, комплексный коэффициент передачи 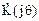, АЧХ K(f_N) и ФЧХ φ(f_N) цифрового фильтра, где θ = 2π f_N, f_N=f/F_Д - нормированная частота.

Построить графики АЧХ и ФЧХ

1. Из рисунка видно, что

=

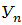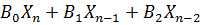
2. Воспользовавшись свойствами Z-преобразования, перейдем от разностных уравнений к уравнениям для Z-преобразований дискретных сигналов v_n, x_n, y_n

= .

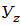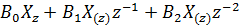Разделив Y(z) на X(z), получим системную функцию цифрового фильтра

=

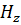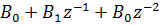
3. Для нахождения комплексного коэффициента передачи фильтра подставим в выражение системной функции 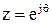, где j – мнимая единица,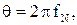 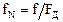- нормированная частота

.= =

[

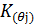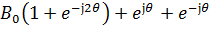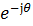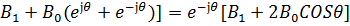
4. Определим АЧХ фильтра

K(θ)=| |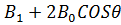

5. Определим ФЧХ фильтра

Φ(θ)=-θ+arg(A(θ))

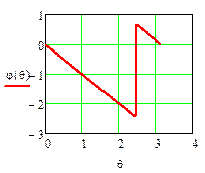
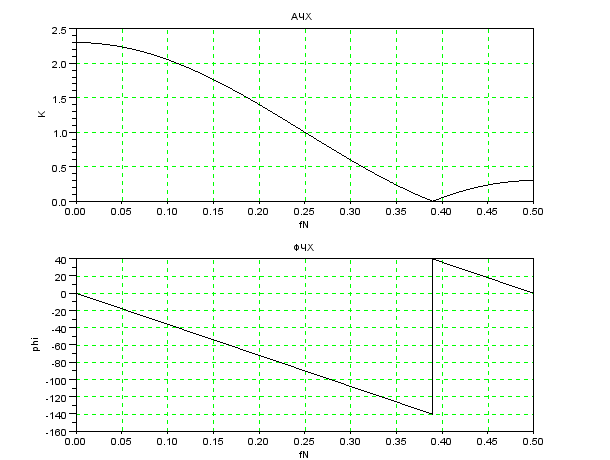
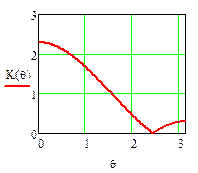
Построим график АЧХ (рисунок 5) при изменении f_N от 0 до 0.5 с шагом 0.0001. Принятый интервал изменения f_N соответствует интервалу частот от 0 до 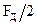. Внутри этого интервала (кроме частоты 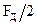) выполняется теорема Котельникова.

Из графика АЧХ следует, что данный фильтр является режекторным. Его коэффициент передачи равен нулю при f_N =0.25, т.е. на частоте, равной четверти частоты дискретизации.

ПРИЛОЖЕНИЕ Б

Программа расчета АЧХ и ФЧХ

// Программа расчета АЧХ и ФЧХ цифрового фильтра рисунка 5B0=0.65B1=1delta_f=0.0001fN=0:delta_f:0.5mmax=0.5/delta_ffor m=1:mmax+1 z=%e^(%i*(m-1)*2*%pi*delta_f); H=B0+B1*z^(-1)+B0*z^(-2); // Системная функция фильтра K(m)=abs(H); phi(m)=atand(imag(H),real(H));endclf()subplot(2,1,1)xtitle("АЧХ", "fN","K")plot(fN,K,"k")xgrid(3) subplot(2,1,2)xtitle("ФЧХ","fN","phi")plot(fN,phi,"k")xgrid(3)

Задание №3.Синтез нерекурсивного цифрового ФНЧ с линейной ФЧХ и гауссовской АЧХ методом ряда Фурье. Моделирование фильтра при действии на его входе полезного сигнала и помехи

Таблица 3. Параметры фильтра, сигнала и помехи

Номер варианта	fNg	σ	δm, дБ	n0	Xp	fNp
	0.05		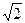-30			0.25

Требуется выполнить синтез цифрового ФНЧ с линейной ФЧХ и АЧХ, выражаемой функцией Гаусса. Требуемая АЧХ фильтра выражается следующим соотношением

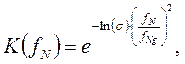
где 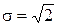- неравномерность АЧХ в полосе пропускания,

f_Ng – нормированная граничная частота полосы пропускания фильтра.

Максимальный уровень пульсаций в полосе задерживания фильтра δm = -30 дБ.

Требуется выполнить моделирование процесса фильтрации при действии на входе фильтра полезного сигнала и помехи.

Полезный сигнал представляет собой случайную последовательность элементарных посылок с уровнями 1 и -1. Количество отсчетов в элементарной посылке равно n0 = 10.

Амплитуда синусоидальной помехи Xp = 1, нормированная частота помехи равна f_Np=0.25.

Схема фильтра приведена на рисунке 9.

дано графическое представление алгоритма реализации нерекурсивного цифрового фильтра с линейной ФЧХ. Линейность ФЧХ обусловлена симметрией коэффициентов b относительно середины линии задержки. Длина линии задержки (количество элементов задержки) равна 2К0.

Синтез фильтра сводится к определению К0 и коэффициентов системной функции фильтра b.

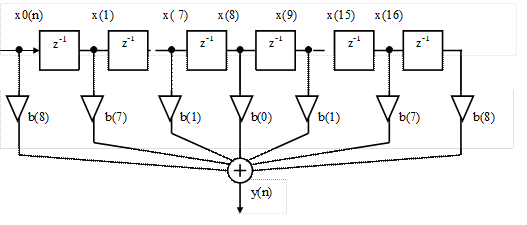
Рисунок 7 – Нерекурсивный фильтр с линейной ФЧХ

Видно, что выходной сигнал фильтра y_n связан с входным сигналом x_n следующим соотношением

.

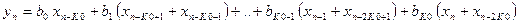Выразим Z – преобразование выходного сигнала фильтра Y(z) через Z – преобразование входного сигнала X(z)

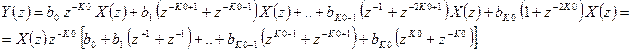
Системная функция фильтра определяется следующим соотношением

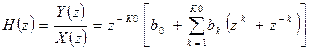
Подставляя в последнее соотношение 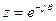, найдем комплексный коэффициент передачи фильтра

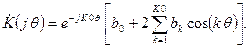
Обозначим

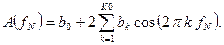(1)

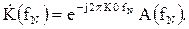Тогда (2)

Найдем АЧХ – зависимость модуля комплексного коэффициента передачи от частоты 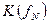и ФЧХ – зависимость аргумента комплексного коэффициента передачи от частоты :

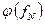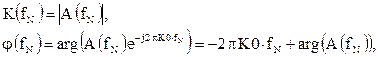(3)

где

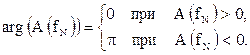
Из последнего соотношения следует, что ФЧХ фильтра является линейно-ломаной.

Из (1) и (3) видно, что АЧХ фильтра является периодической функцией нормированной частоты с периодом, равным единице (или периодической функцией частоты с периодом, равным частоте дискретизации).

Последнее означает возможность синтеза цифровых фильтров путем разложения функции, описывающей требуемую АЧХ в ряд Фурье, где коэффициенты b₀ и 2b_k являются коэффициентами Фурье. На рисунке 26 приведена требуемая АЧХ фильтра в интервале от нуля до 0.5 и её продолжение вдоль оси нормированных частот

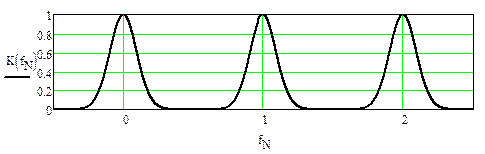
Используя выражения для коэффициентов Фурье четной функции K(f_N) и сопоставляя их с коэффициентами системной функции в соотношении (1), получим

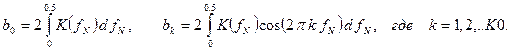(4)

Синтез фильтра выполнен по программе «FilterGauss». sce.

Результаты синтеза:

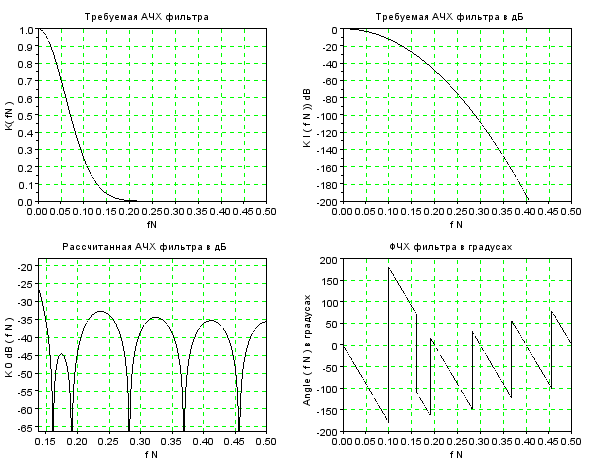
Рисунок8 – АЧХ и ФЧХ при K0 = 5

Коэффициенты системной функции приведены в таблице 5

Таблица 5 – Коэффициенты системной функции фильтра

Номер коэффициента k	Значение коэффициента b(k)
	0.1505384
	0.1401935
	0.1132323
	0.0793184
	0.0481881
	0.0253902

Повторение эксперимента при K0=8

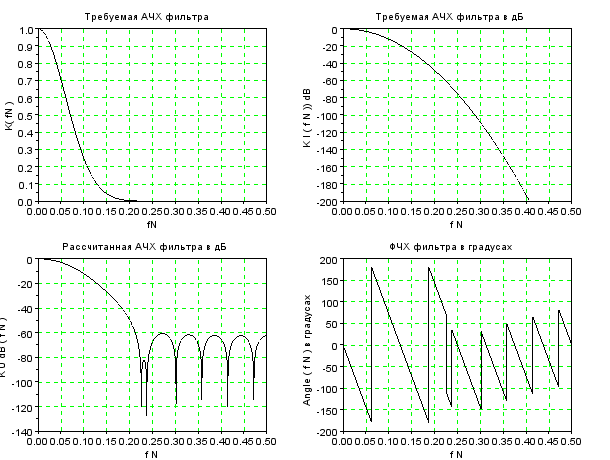
Рисунок 9 – АЧХ и ФЧХ при K0 = 8

Повторение эксперимента при K0=3

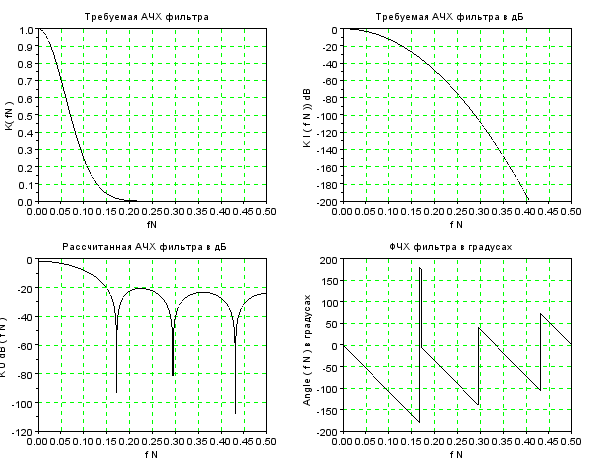
Рисунок 10 – АЧХ и ФЧХ при K0 = 3

Изменяя длину линии задержки, можем сделать вывод о том, что при ее увеличении в 1.5 раза увеличиваются пульсации на рассчитанной АЧХ , а при уменьшении в 1.5 раза- уменьшаются пульсации на рассчитанной АЧХ.

Таблица – Влияние длины линии задержки на ослабление в полосе задерживания

K0	δ в дБ
	-33
	-20
	-60

АЧХ фильтра определяется следующим соотношением:

.

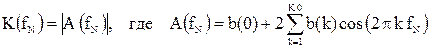ФЧХ фильтра без приведения в интервал от – π до π , определяется соотношением

.

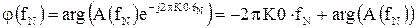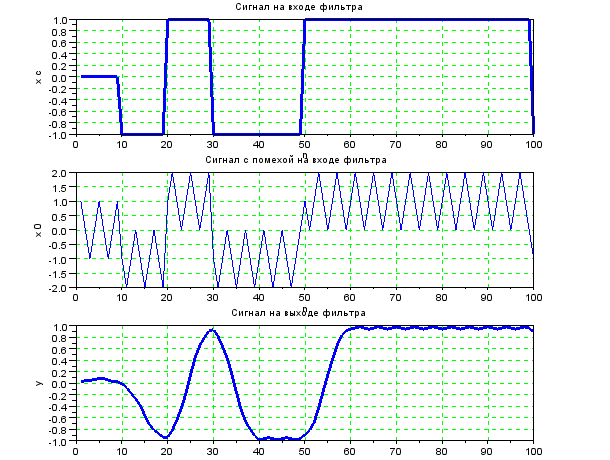
Рисунок 11 – Временные диаграммы входного сигнала, входного сигнала

с помехой и выходного сигнала

Результаты моделирования позволяют сделать следующие выводы:

· Фильтр позволяет с высокой степенью скорректировать негативное влияние помехи, поданной на вход с полезным сигналом;

· Сигнал на выходе фильтра

·

ПРИЛОЖЕНИЕ В

Программа синтеза нерекурсивного цифрового гауссовского ФНЧ

//Программа синтеза нерекурсивного цифрового гауссовского ФНЧ ////Ввод исходных данныхK0=5 //Половина длины линии задержкиfNg=0.05 //Нормированная граничная частота фильтраsigma=sqrt(2) //Неравномерность АЧХ в полосе delta_m=-30 //Максимальный уровень пульсаций в дБ// Функция, описывающая требуемую АЧХ фильтра в интервале // нормированных частот от 0 до 0.5function u=K(fN), u=exp(-log(sigma)*(fN/fNg)^2) endfunction;// Функция, описывающая требуемую АЧХ фильтра в интервале // нормированных частот от 0 до 0.5, заданную в дБ function ul=KdB(fN), if K(fN)>10^-10 then ul=20*log10(K(fN)) else ul=-200 end endfunctiondelta_f=0.0001 //Шаг изменения частоты при расчете АЧХ и ФЧХ I=ceil(0.5/delta_f)// Количество расчетных точек АЧХ на графикахi=[1:I+1] // Массив номеров расчетных точекfN=(i-1)*delta_f // Массив значений частот при расчете АЧХy=zeros(1:I+1); // Обнуление массивов y и y1y1=zeros(1:I+1);for i=1:I+1 // Формирование массивов значений АЧХ в расчетных // точках y(i)=K(delta_f*(i-1)) yl(i)=KdB(delta_f*(i-1))end;clf()// Очистка графического окна перед выдачей графиков// Построение графика требуемой АЧХ в относительном масштабеsubplot(221)xtitle("Требуемая АЧХ фильтра", "fN","K( fN )" )plot(fN,y,"k")xgrid(3)// Построение графика требуемой АЧХ в дБsubplot(222)xtitle("Требуемая АЧХ фильтра в дБ", "f N","K l ( f N )) dB" )plot(fN,yl,"k")xgrid(3)//Формирование массива коэффициентов системной функции фильтраb0=2*intg(0,0.5,K)// Расчет коэффициента b0b=zeros(1:K0)function w=KC(fN, k), w=2*K(fN)*cos(2*%pi*k*fN),endfunctionfor k=1:K0 b(k)=intg(0,0.5,KC)end//Системная функция цифрового фильтраfunction v=H(z)v=b0for k=1:K0 v=v+b(k)*(z^k+z^-k)endv=v*z^-K0endfunction//Расчет зависимости комплексного коэффициента передачи фильтра // от частоты, АЧХ и ФЧХKk=zeros(1:I+1)for i=1:I+1 z=%e^(%i*2*%pi*delta_f*(i-1)) Kk=H(z) // Комплексный коэффициент передачи if abs(Kk)>10^-10 then K0dB(i)=20*log10(abs(Kk))// АЧХ else K0dB(i)=-200 end fi(i)=atand(imag(Kk),real(Kk)) // ФЧХ end// График АЧХsubplot(223)xtitle("Рассчитанная АЧХ фильтра в дБ", "f N","K 0 dB ( f N )" )plot(fN,K0dB,"k")xgrid(3)//График ФЧХsubplot(224)xtitle("ФЧХ фильтра в градусах", "f N","Angle ( f N ) в градусах" )plot(fN,fi,"k")xgrid(3)// Выдача на дисплей значений коэффициентов системной функцииdisp(b0)disp(b)

Поволжский Государственный Университет Телекоммуникаций и Информатики

Курсовая работа по предмету «Цифровая обработка сигналов»

Выполнил:

Студент гр.М-11;ФЗО

Фадеев Д.В.

Проверил:

К.т.н., доцент

Иванова В.Г.

Самара