Итерационный цикл с рекуррентной зависимостью

Для вычисления на компьютере сумм бесконечного ряда часто используют рекуррентные формулы, с помощью которых друг за другом вычисляют значения членов бесконечной последовательности. Рекуррентные формулы существенно сокращают время работы программы, упрощают процесс написания программы и ее отладки. Как правило, рекуррентные формулы программист должен составить сам. В этом и состоит искусство программирования вычислительных процессов. Рекуррентная формула может и отсутствовать. В этом случае каждый член ряда придется рассчитывать “в лоб” по полной формуле.

Есть определенные признаки, которые помогают выявить наличие рекуррентных формул. К таким признакам относятся выражения 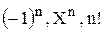и подобные этим выражения, присутствующие в формуле общего члена бесконечного ряда. Часто рекуррентная формула для бесконечного ряда находится путем деления соседних членов ряда друг на друга.

Задача 8. Вычислить 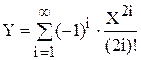. Вычисление ряда окончить при выполнении условия .

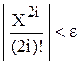Для решения этой задачи необходимо использовать рекуррентную формулу. А найти ее можно следующим способом. Сделаем преобразование исходного ряда в следующий вид: . Тогда условие окончания вычислений будет выглядеть так . Это условие либо выполнится для некоторого i = n, и вычислительный процесс будет завершен, или не выполнится. Во втором случае используют термин “зависание программы”. Оператор ЭВМ искусственно останавливает программу и выясняет причину зависания: неправильные исходные данные, например, комбинация X и ε, или допущена ошибка в тексте программы, а может быть, получена неправильная рекуррентная формула, или другая причина имеет место.

Нас в этом примере интересует нормальный режим работы программы, а это означает, что существует такое n, для которого справедливы следующие формулы:

(5)

Эти формулы и будут исходными для нашей задачи. На этом первый этап подготовки бесконечного ряда к нахождению его суммы Y с погрешностью ε на компьютере завершается. Если рекуррентную формулу найти невозможно или нет в этом необходимости, то можно ограничится только приведенными выше преобразованиями.

Но в нашем случае нужен второй этап преобразования, а именно, нахождение рекуррентной формулы. Для этого поделим два соседних члена .

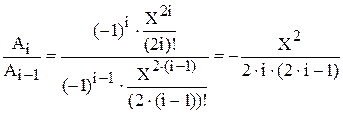(6)

Из (6) и находится рекуррентная формула:

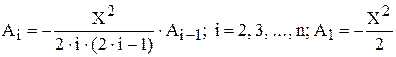(7)

Таблица имён

Математ. величина	Обозначение в программе	Содержательный смысл	Тип переменной
i	i	Номер итерации	вещественный
X	X	Параметр бесконечного ряда	вещественный
Y	Y	Искомая сумма	вещественный
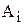	A	Член последовательности A с номером i	вещественный
ε	E	Требуемая точность расчетов	вещественный

Блок-схема алгоритма решения задачи представлена на рис. 8.

Код программы – процедура pr8.

Рис. 8. Блок-схема алгоритма решения задачи 8

Sub pr8()

Dim Y As Double, X As Double, E As Double, A As Double

Dim i As Double

X = InputBox(“X=”)

E = InputBox(“E=”)

i =1 : A= -X*X/2 : Y = 0

Do While Abs(A) >= E

Y = Y + A

i=i+ 1

A = -X*X / 2 / i / (2*i - 1)*A

Loop

MsgBox(“Y=” & Y)

End Sub