Математическая постановка задачи

АНАЛИЗ РЕЗУЛЬТАТОВ И ВЫВОДЫ

Введение

Цель курсовой работы: закрепление знаний и умений по алгоритмизации и программированию на языке Си с использованием функций, процедур и различных сложных типов данных, в том числе динамических массивов, структур и объединений.

Назначение и область применения программы: программа будет использоваться в учебном процессе для решения инженерных задач обработки массивов, путём её включения в программы пользователей.

Задание на курсовую работу

Содержательное описание задачи

Для первой задачи даны три функци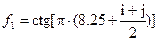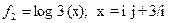и , и 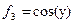. Нужно будет найти элементы матрицы A по формуле:

,

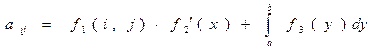где x=f(i,j) – аргумент функции 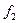, a,b – пределы интегрирования функции .

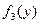Функция 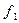представляет собой арифметическую функцию, проблем с ее вычислением в принципе не должно возникнуть.

Функцию f₂ следует продифференцировать.

Функция f₃ есть подынтегральное выражение, которое является тригонометрическим выражением, вычисление будет производиться по формуле:

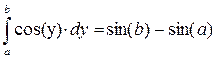
a, b – нижний и верхний интеграл соответственно

К моменту выполнения второй задачи будет сформирована матрица. Задача состоит в том, чтобы сформировать вектор, состоящий из наибольших среди отрицательных элементов i^-го столбца.

При решении первой задачи получим квадратную матрицу, т.е. матрицу. a которой число строк равно числу столбцов.

Третья задача представляет собой набор матричных операций. Необходимо перемножить три операнда, представленных в виде особого вида матрицы или вектора, а также некоторых действий над ними.

Рассмотрим эти операции.

Сначала нужно получить вектор, состоящий из обратных элементов вектора, полученного во второй части.

Вторым операндом будет квадрат разности исходной и транспонированной исходной матриц

Произведением матрицы A_m*n = (a_ij) на матрицу B_n*p = (b_jk) называется матрица C_m*p = (c_ik) такая, что

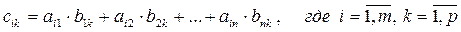
т.е. элемент i-й строки и k-го столбца матрицы произведения C равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы k-го столбца матрицы B.

В качестве 3 операнда будет 1/D – вектор, составленный из обратных элементов главной диагонали матрицы А.

Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается A^T.

В четвёртой задаче надо произвести стандартные арифметические действия над элементами матрицы, сформированной в первой задаче.

Математическая постановка задачи

Задание состоит из 4-х задач:

1.- формирование элементов матрицы A с помощью функций.

2. - формирование вектора X из элементов матрицы A,

3. -матричные операции: Z =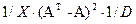

4. - комплексное преобразование массивов Y= +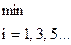

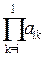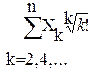
2.3. Интерфейс ввода/вывода

Данные будем вводить с клавиатуры, а результаты в файл.