Программирование алгоритмов разветвленной структуры

Цель работы:изучить операторы условного и безусловного перехода иприобрести практические навыки в программировании алгоритмов разветв-ленной структуры.

Задание:

1. Изучить операторы условного и безусловного перехода языка Бейсик и особенности их применения.

2. Для заданного варианта составить схему алгоритма разветвленной структуры и реализующую его программу с использованием операторов условного и безусловного перехода.

3. Произвести на ЭВМ расчеты по разработанной программе для исходных данных, приведенных в табл. 3.1.

4. Получить распечатку программы и результатов расчета.

5. Оформить отчет по лабораторной работе.

Указания по выполнению работы

Алгоритм разветвленной структуры включает в себя одну из основных структур: разветвление (рис.3.1,а) или обход (рис.3.1,б) Разветвление приме-няется, когда в зависимости от некоторого условия ("да" - условие истинно, "нет" - условие ложно) нужно выполнить либо действие 1, либо действие 2, которые, в свою очередь, могут содержать несколько этапов расчета. Обход является частным случаем разветвления, когда одна ветвь не содержит ни каких действий.

При программировании алгоритмов разветвленной структуры следует иметь в виду, что в схеме алгоритма ветви с разными действиями парал-лельны, а в программе эти действия должны следовать друг за другом, причем, если действие одной ветви выполнено, то действие другой ветви не выпол-няется.

Организация разветвления или обхода в программах, осуществляется с помощью операторов безусловного перехода GO ТО и условного перехода IF.

Общий вид оператора безусловного перехода

GO ТО n

где n - номер строки.

Оператор безусловного перехода передает управление первому опера-тору в строке с меткой n.

	Да		Условие		Нет
Действие 1					Действие 2

1. Если < условие > выполняется перейти к п.4

2. Операторы действия 2

3. перейти к п.5

4. Операторы действия 2

5. …

а)

Да	Условие	Нет
		Действие

1. Если < условие > выполняется перейти к п.3

2. Операторы действия

3. …

б)

Рис.3-1. Виды условных конструкций и их программирование с использова-нием условного оператора IF:

а - структура разветвление; б - структура обход.

Оператор условного перехода может быть записан в линейной или блочной формах.

Линейная форма записи:

IF логическое выражение THEN операторы 1 ELSE операторы 2

где логическое выражение - выражение, возвращающее ненулевые значения (истина) или ноль (ложь); операторы 1 – операторы, выполняющиеся при значении логического выражения “истина”; операторы 2 - при значении “ложь”. Блок ELSE и операторы 2 может отсутствовать , тогда при значении логического выражения “ ложь” осуществляется переход к первому оператору следующей строки. Если предполагается проверять больше, чем два условия, то целесообразно применять блочную форму оператора IF…THEN…ELSE.

Блочная форма записи:

IF логическое выражение 1 THEN операторы 1

[ ELSEIF логическое выражение 2 THEN операторы 2 ]

………………………………………………

[ ELSE

операторы n ]END IF

где логические выражения 1 и 2 – выражения, аналогичные логическому выражению в линейной форме записи; операторы 1 - одна или более строк операторов, выполняющихся при условии логическое выражение 1 - “исти-на”; операторы 2 - одна или более строк операторов,выполняющихся приусловии логическое выражение 2 - “истина”; операторы n - одна или более строк операторов, выполняющихся при прочих условиях.

При блочной форме записи первоначально тестируется первое логиче-ское выражение. Если оно не нулевое (“ истина”), то выполняются операторы 1.Если первое выражение равно нулю(“ложь”),то оценивается каждое ус-ловие ELSEIF. При выполнении такого условия выполняются операторы данного блока (в нашем случае операторы 2). Если ни одно из условий ELSEIF не выполняется (все = “ложь”), то выполняются операторы n блока ELSE. Блоки ELSEIF и ELSE могут быть опущены. Операторы IF, ELSE, ELSEIF и END IF должны быть первыми операторами в строке. Блок должен заканчиваться оператором END IF.

В качестве примера на рис.3.2 приведены алгоритм вычисления функции

sin x,	если x ≤0
y =	+ln x,	если x >0
1

и соответствующая ему программа, иллюстрирующая применение условного оператора IF.

Да

Y=sin x

Начало			REM Программа расчета функции с
					REM применением условного оператора
					PRINT “Введите значение X=”;
Ввод x			INPUT X
					IF X<=0 THEN
					Y=SIN(X)
X<=0		Нет	ELSE
			Y=1+LOG(X)
					END IF
			Y=1+ln x	PRINT “Значение функции Y=”;Y
					END
					б )
				Рис. 3.2. Пример программирования ал-
Вывод

^Y 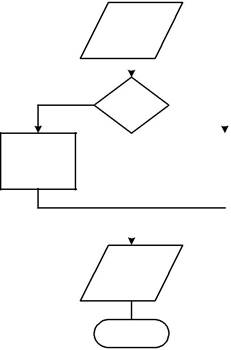горитма разветвленной структуры:

а – схема алгоритма; б – его программная

Конец	реализация с использованием условного
а)	перехода IF.

Таблица 3.1

Варианты заданий к лабораторной работе № 3

№	Составить программу вычисления значений	Исходные данные
п.п													функций	a	x	y
1.	1 + tg x,		если a ≤0	-1,25	0,56	-
	z =		− 2 y,		если a >0	6,34	4,27	-10,6
	x 2
2.	3 y − cos x,	если x ≤0	-	-2,93	17,5
	z =									если x >0	4,25	3,61	2,58
	ax 2+ y ,
3.	2sin 2 x ⋅ cos y,	если x ≤ y	-	3,64	4,47
	z =		− y 2 ,		если x > y	-	4,89	1,36
	x 2
4.	3a − arctg x,		если a >0	12,8	0,56	-
	z =		− 9 a,		если a ≤0	-9,52	5,48	-
	x 2
5.	(2 y + 1)sin x,	если x <0	-	-3,68	8,34
	z =		+ 4 y − a ,	если x ≥0	12,8	5,26	34,2
	x 3
6.	y ln		x		+a,	если x <0	-25,6	-7,43	11,2
	z =									если x ≥0	-	3,25	-6,45
	2 y + ex ,
7.	x tg x +3a,	если x > a	1,37	1,83	-
	z =	+ y − a ) 2 ,	если x ≤ a	5,21	3,15	38,5
	( x
8.	3 x / lg y + 2 a,	если y >0	7,48	-21,4	49,1
	z =		− x / a,	если y ≤0	8,34	11,5	-9,15
	y 3
9.	(1 − x )cos ay,	если x >1	0,33	2,63	3,42
	z =		− 5 y − 6 a,	если x ≤1	4,16	-6,48	0,24
	x 2
10.	2 y + sin x,	если x <0	-	-3,68	8,34
z =
	x 3		− 4 ya,	если x ≥0	12,8	5,26	34,2
11.	y cos x + a ,	если x <0	-25,6	-7,43	11,2
z =
	2 y + ex ,		если x ≥0	-	3,25	-6,45
12.	x sin x +3a,	если x > a	1,37	1,83	-
z =
	( x 2 + y − a ) 2 ,	если x ≤ a	5,21	3,15	38,5
13.	3 x / sin y + 2 a,	если y >0	7,48	-21,4	49,1
z =
	y 2		− x / a,	если y ≤0	8,34	11,5	-9,15
14.	(1 − sin x )cos ay,	если x >1	0,33	2,63	3,42
z =
	x 2		− 5ay,	если x ≤1	4,16	-6,48	0,24
	cos 2,5 x + lg y,	если y >1	Исходные данные
	x	y	z
15.	u =
	+ 6 y	− 4,3 z,	если y ≤1	0,23	9,36	-
	2 x
														3,57	-27,4	19,2

16.		1,	если x < y			-5,27	36,2	-
	u =			если x = y			22,8	22,8	-
	0,
						если x > y			57,3	33,8	-
		− 1,
17.	u =min{x , y}					5,21	4,44	-
18.	u =max{x , y}				3,25	0,91	-
19.	u =min{x , y , z}				74,3	34,7	13,5
20.	u =max{x , y , z}				0,24	7,63	5,85
21.	u =max{x , y}−min{y , z}		57,3	81,9	64,5
22.	u =max{x , y}+min{y , z}		-30,7	3,74	23,7
23.	u =max{x , y}/ min{y , z}			9,56	7,83	5,89
24.	u =max{x , y}⋅min{y , z}			-2,12	1,12	6,14
25.		max	{	x , y ,	если z ≥0	2,96	3,15	8,69
	u =					}
								если z <0	1,85	4,02	-19,7
		x sin y − z ,
26.		min	{	x , z	,	если y ≥3	74,3	18,8	23,8
	u =					}
			+ ln z,	если y <3	65,7	-67,3	12,7
		3 xy
27.									если z	≥		75,4	85,3	40,8
	u =	max {x , y},
	min	{ x , y},	если z <2	32,7	48,2	0,67
28.									если y	>		17,5	38,2	-
	u =	max {x , y},
	min	{ y , z},	если z ≤0	-	-35,9	-64,2
29.	u =max{x , y , z}+min{x , y , z}	6,84	35,4	99,1
30.	u =max{x , y , z}/ min{x , y , z}	84,3	56,9	11,4

Лабораторная работа № 4