Алгоритмы списочных расписаний

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра “Программное обеспечение вычислительной техники и автоматизированных систем”

Методические указания

и контрольные задания к практическим, лабораторным занятиям, курсовому проектированию по теме «Теория расписаний», для дисциплин «Алгоритмические языки и программирование», «Вычислительная техника и программирование»

Ростов-на-Дону

Общие сведения

Предметом области исследования расписаний является круг задач проектирования и организационного управления в различных системах, в которых требуется найти наилучшее (оптимальное) значение выбранных критериев их функционирования с учетом имеющихся ограничений.

Программирование для многопроцессорных машинных систем связано с распараллеливанием и синхронизацией вычислений и организацией выполнения параллельных вычислительных процессов. Это выдвигает целый ряд сложных задач, среди которых весьма важными являются, расчет характеристик времени и количества операций, требующихся для выполнения параллельных программ, и построения расписаний (планов), выполнения параллельных программ на многопроцессорных и многомашинных вычислительных системах.

Модели параллельных программ и операционные характеристики процессов их выполнения служат основой для планирования параллельных вычислительных процессов, т.е. для построения расписаний указанных процессов. Расписания параллельных вычислительных процессов определяют порядок выполнения программы на вычислительной системе, включая распределение частей программы по процессам. С увеличением числа распределяемых частей программ и количества используемых процессоров сложность построения оптимальных расписаний обычно резко возрастает. Поэтому важное значение имеют простые в построении и удобные в реализации приближенные расписания параллельных вычислительных процессов, близкие к оптимальным с точки зрения времени выполнения параллельных программ.

Постановка задачи

Имеется вычислительная система (ВС), состоящая из 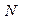несвязанных идентичных устройств (приборов, процессоров и т.п.)

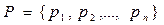
На обслуживание в ВС поступает набор из 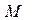независимых параллельных заданий (работ) 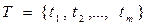известно время решения 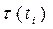задания 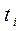на любом из устройств. При этом каждое задание может выполняться на любом из устройств (процессоре), в каждый момент времени отдельный процессор обслуживает не более одного задания и выполнение задания не прерывается для передачи на другой процессор. Требуется найти такое распределение заданий по процессорам, при котором суммарное время выполнения заданий на каждом из процессоров было бы минимальным. Под расписанием следует понимать отображение 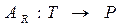, такое что, если 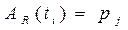, то говорят что задание 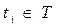, в расписании 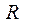назначенного на процессор 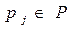. 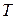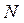При сделанных выше допущениях, расписание можно представить разбиением множества заданий на непересекающихся подмножеств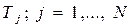

Критерий, используемый для минимизации времени завершения обслуживания заданий, является минимальным критерием и определяется в следующем ви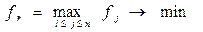де: , где

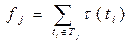- время завершения работы процессора .

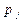Задача №1

Для примера рассмотрим задачу 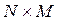, где 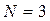, 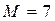. Исходный вектор заданий 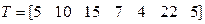. Решим приведенными ниже алгоритмами, нахождения расписаний.

Алгоритмы списочных расписаний