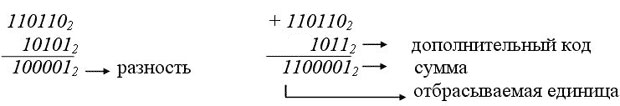Для изображения десятичных дробей используется подобная формула разложения по степеням основания.

Пример. 110,001₂ = 1x2² + 1 x 2¹ + 0 x 2⁰ + 0 x 2^-1 + 0 x 2^-2 + 1 x 2^-3 = 6,125₁₀ ;

A,B₁₆ = A x 16⁰ + B x 16^-1 = 10 x 1 + 11 x 0,0625 = 10,6875₁₀ .

Практика. Перевод в 10-ую систему, дробные числа

357,12(8) = 239,1563

471,47(8) =313, 6094

121,7(8) =81,875

AB,CD(16) =171,7669

C23,7F(16) =3107,496

DE,EE(16) =222, 9297

110,111(2) =6,875

001,100(2) =1, 5

11001,11(2) = 25, 75

111,011(2) = 7, 375

Процедура перевода десятичных чисел в р-ную систему счисления:

1. перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]₁₀ , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р ; изображение [х]_p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
2. перевести отдельно дробную часть (мантиссу) числа, то есть {x}₁₀ , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}_p ; изображение {х}_p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
3. результат будет иметь вид (х)_р = [х]_p, {х}_p .

Пример. Найти: 12,8₁₀ = ?₂ . Решение:

1. Переводим целую часть: 12₁₀ =1100₂;
2. переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,8₁₀ = 0,1100110...₂ ;
3. результат перевода: 12,8₁₀ = 1100,1100110011...₂ .

Пример. Найдем 29,25₁₀ = ?₈ . Решение имеет вид 1) 29₁₀ = 35₈ ; 2) 0,25₁₀ = 0,2₈ ; 3) 29,25₁₀ = 35,2₈ .

Пример. Найдем 79,26₁₀ = ?₁₆ . Решение: 1) 79₁₀ = 4F₁₆ ; 2) 0,26₁₀ = 0,40₁₆ ; 3) 79,26₁₀ = 4F,4₁₆ . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.

Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:

ОСНОВАНИЕ СИСТЕМЫ
	—
	—
	—
	—
	—
	—
	—	—
	—	—
	—	—
	—	—
	—	—
	—	—
	—	—
	—	—

При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их.

Пример. Рассмотрим переводы в смешанных системах.

1. Из 2-ной системы в 8-ную (двоично-восьмеричное изображение):

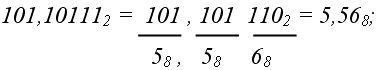
2. из 8-ной системы в 2–ную (восьмерично-двоичное изображение):

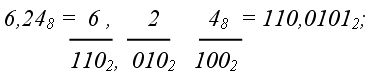
3. из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):

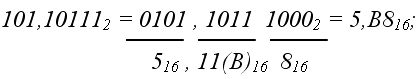
4. из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):

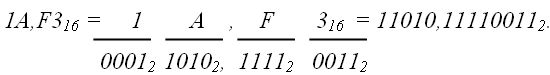
Практика: Синие цифры даны, остальные посчитать

10 ->p ЦЕЛОЕ = частное от деления на p (значения в обратном порядке) ДРОБНОЕ = целое от умножения ма нтиссы на p(значения в прямом порядке

p->10 число из разряда УМНОЖИТЬ p в степени разряда , для дроби минусовая степень

				AB
				2E1
				CDE
	54,12	110110,0001	66,0753	36,1
	127,2969	1111111,0100	177,23	7F,4С
	205,6641	11001101,1010	315,524	CD,AA
	56,17	111000,0010	70,1270	38,28

Сложение в двоичной системе счисления осуществляется по правилам

0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 2₁₀ = 10₂ (единица идет в старший разряд).

Таблица вычитания в двоичной системе счисления имеет вид

0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда).

Таблица умножения в двоичной системе счисления имеет вид

0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1.

Таблица деления в двоичной системе счисления имеет вид

0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1.

Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р – 1 ).

Дополнительный код = обратный код + единица в младшем разряде.

Пример.

1. 10011 двоичное число,

01100 обратный код этого двоичного числа,

01101 дополнительный код этого двоичного числа;

2. 457 восьмеричное число,

321 дополнительный код ;

3. А9 шестнадцатеричное число,

57 дополнительный код.

Вычитание с помощью дополнительного кода: найти дополнительный код вычитаемого такой же разрядности, как и уменьшаемое, и сложить этот код с уменьшаемым. Результатом вычитания будет полученная сумма без учета старшего разряда (отбрасывается).

Пример. Выполним вычитание напрямую и через сложение (через дополнительный код ):