Для продолжения нажмите любую клавишу

Задача 5.2

Постановка задачи

Функцияu(x), являющаяся решением краевой задачи

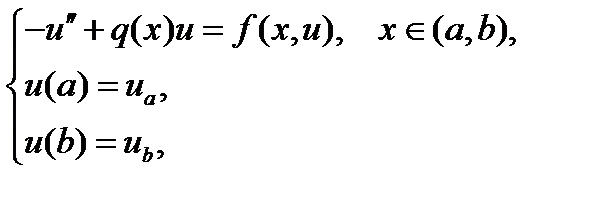
описывает стационарное распределение тепла в одномерном стержне, совпадающем с отрезком .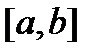

Рассчитать стационарное поле температур на отрезке 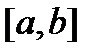. Предусмотреть возможность задания произвольных граничных условий. Для проверки работы программы построить и рассчитать тестовый пример.

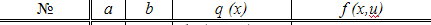
5.2.11

2.2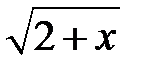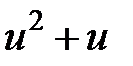

Решение

1. Построим тестовый пример.

Выберем в качестве точного решения некоторую непрерывную функцию: u(x)=1-x². Очевидно, что значение u(a)=u(0)= -1. Это значит, что в тестовом примере u_a=1. Аналогично, u_b=-3.84.

Построим правую часть тестового примера. Для этого найдем левую часть уравнения при выбранной функции u(x).

g(x) = -u”(x) + q(x)*u(x) = 2 + (2+x)^(1/2)*(1-x²) = 2+(2+x)^(1/2)-(x^2)* *(2+x)^(1/2).

Этому же должна быть равна и правая часть уравнения, составляющая сейчас:

f(x) = (u(x)^2 + u(x)) = 2 – 3*x^2 + x^4.

Ясно, что равенства можно добиться, добавляя в правую часть слагаемое

s(x) = g(x) – f(x) =(2+x)^(1/2) - (x^2)*(2+x)^(1/2) + 3*x^2 - x^4

Таким образом, построен тестовый пример:

-u”+xu = u^2+u + (2+x)^(1/2) - (x^2)*(2+x)^(1/2) + 3*x^2 - x^4 x ϵ (0, 2.2),

u(0) = 1,

u(2.3) = -3.84.

Решением построенной задачи является функция u(x)=1-x².

2. Проверим правильность работы программы на тестовом примере.

Посчитаем значения функции u(x) в точках 0.575, 1.15, 1.725.

u(0.55) = 1-0.55² = 0.6975,

u(1.1) = 1 - 1.1² = -0.21,

u(1.65) = 1 - 1.65² = -1.7225.

Результаты программы совпадают с вычислениями, значит, программа работает корректно.

Введите количество разбиений отрезка [a,b]

Введите точность эпсилон

0.00001

Введите значение в точке а

Введите значение в точке b

-3.84

Ua: 1, Ub: -3.84

Деления отрезка:

0 0.55 1.1 1.65 2.2

Матрица производных:

1 0 0 0 0

-1 2.78555 -1 0 0

0 -1 2.83511 -1 0

0 0 -1 2.88043 -1

0 0 0 0 1

Наддиагональ:

0 -1 -1 -1 0

Поддиагональ:

0 -1 -1 -1 0

Главная диагональ:

1 2.78555 2.83511 2.88043 1

Правая часть:

0 3.06682 1.07594 -3.02901 0

Начальное значение:

1 -1 -1 -1 -3.84

Ответ:

1 0.6975 -0.21 -1.7225 -3.84

Для продолжения нажмите любую клавишу . . .

3. Решим данную задачу. Граничные условия зададим такие: u(0) = -1, u(2.2) = -11.

Введите количество разбиений отрезка [a,b]

Введите точность эпсилон

0.000001

Введите значение в точке а

-1

Введите значение в точке b

-11

Ua: -1, Ub: -11

Деления отрезка:

0 0.244444 0.488889 0.733333 0.977778 1.22222 1.46667 1.71111 1.95556 2.2

Матрица производных:

1 0 0 0 0 0 0 0 0 0

-1 2.14927 -1 0 0 0 0 0 0 0

0 -1 2.15402 -1 0 0 0 0 0 0

0 0 -1 2.15854 -1 0 0 0 0 0

0 0 0 -1 2.16286 -1 0 0 0 0

0 0 0 0 -1 2.16701 -1 0 0 0

0 0 0 0 0 -1 2.17101 -1 0 0

0 0 0 0 0 0 -1 2.17486 -1 0

0 0 0 0 0 0 0 -1 2.17859 -1

0 0 0 0 0 0 0 0 0 1

Наддиагональ:

0 -1 -1 -1 -1 -1 -1 -1 -1 0

Поддиагональ:

0 -1 -1 -1 -1 -1 -1 -1 -1 0

Главная диагональ:

1 2.14927 2.15402 2.15854 2.16286 2.16701 2.17101 2.17486 2.17859 1

Правая часть:

0 0.0895189 0.0942677 0.0987886 0.103111 0.10726 0.111254 0.11511 -9.88116 0

Начальное значение:

-1 -1 -1 -1 -1 -1 -1 -1 -1 -11

Ответ:

-1 -0.958525 -1.00048 -1.13678 -1.39467 -1.82925 -2.55068 -3.79223 -6.10301 -11

Для продолжения нажмите любую клавишу . . .

4. Листинг программы (только существенные части):

// Значения, стоящие в матрице производных на главной диагонали

void diagElem(double mas[], double z[], double x[], int N)

{

double a = 0; // левая граница стержня

double b = 2.2; // правая граница стержня

double h = (b - a) / N; // шаг

for (int i = 0; i <= N; i++)

{

mas[0] = 1;

if ((i != 0) & (i != N))

mas[i] = (2 + h*h*(sqrt(2 + x[i]))) - h*h*(2 * z[i] + 1);

mas[N] = 1;

}

}

// Функция (правая часть м.Ньютона)

void F(double mas[], double z[], double x[], int N, double grA, double grB)

{

double a = 0; // левая граница стержня

double b = 2.2; // правая граница стержня

double h = (b - a) / N; // шаг

mas[0] = -z[0] + grA;

for (int i = 1; i < N; i++)

{

mas[i] = -(-z[i - 1] + 2 * z[i] - z[i + 1] + sqrt(2 + x[i])*z[i] * h*h - h*h*(z[i] * z[i] + z[i]));

}

mas[N] = -z[N] + grB;

}

// Метод прогонки

void solveProgonka(double x[], double a[], double b[], double c[], double d[], int n)

{

double alpha[nmax], betta[nmax];

alpha[0] = -c[0] / b[0];

betta[0] = d[0] / b[0];

for (int i = 1; i < n; i++)

{

alpha[i] = -c[i] / (b[i] + a[i] * alpha[i - 1]);

betta[i] = (d[i] - a[i] * betta[i - 1]) / (b[i] + a[i] * alpha[i - 1]);

}

betta[n] = (d[n] - a[n] * betta[n - 1]) / b[n] + a[n] * alpha[n - 1];

x[n] = betta[n];

for (int i = n - 1; i >= 0; i--)

{

x[i] = alpha[i] * x[i + 1] + betta[i];

}

}

// Первая норма вектора

double norm1(double x[], int n)

{

double sum;

sum = 0.0;

for (int i = 0; i <= n; i++)

sum = sum + abs(x[i]);

return sum;

}

// Цикл поиска решения

while (norma>eps)

{

// сохраняем старое значение

for (inti = 0; i<= N; i++)

temp[i] = z[i];

// изменяем матрицу производных

diagElem(mainDiag, z, setka, N);

// изменяем правую часть

F(funcF, z, setka, N, ua, ub);

solveProgonka(delta, podDiag, mainDiag, nadDiag, funcF, N);

norma = norm1(delta,N);

//обновляем вектор решения

for (inti = 0; i<= N; i++)

{

z[i]=delta[i]+temp[i];

}

}