Поиск минимального значения функции

В системе MATLAB имеются функции, осуществляющие поиск минимальных значений (минимумов) заданных функций, причем как для функций одной переменной, так и для функций многих переменных.

В частности, для отыскания минимума функции одной переменной используется функция fminbnd:

fminbnd(hFunction,x0,xl)

где hFunction – дескриптор функции, для которой находится минимум; x0 и xl задают границы отрезка поиска.

Рассмотрим использование данной функции на примере поиска минимума многочлена 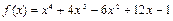на отрезке 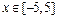. Для построения графика обратимся к функции fplot (рис. 2.21.1):

>> f=inline('x^4+4*x^3-6*x^2+12*x-1','x')

f =

Inline function:

f(x) = x^4+4*x^3-6*x^2+12*x-1

>> fplot(f,[-5 5])

Согласно рис. 2.21.1, минимум рассматриваемой функции 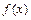существует на отрезке 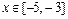. Для нахождения минимума будем иметь:

>> fminbnd(f,-5,-3)

ans =

-3.9514

Для одновременного определения минимума и соответствующего значения 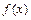в точке минимума следует использовать следующий синтаксис вызова функции fminbnd:

>> [x,y]=fminbnd(f,-5,-3)

x =

-3.9514

y =

-145.0966

Для поиска минимума функции нескольких переменных используется функция fminsearch:

fminsearch(hFunction,x0)

где hFunction – дескриптор функции нескольких переменных, для которой находится минимум; x0 – вектор аргументов функции, с которого начинается поиск минимума.

Продемонстрируем использование данной функции на примере поиска минимума функции 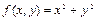. Имеем:

>> f=inline('x(1)^2+x(2)^2','x')

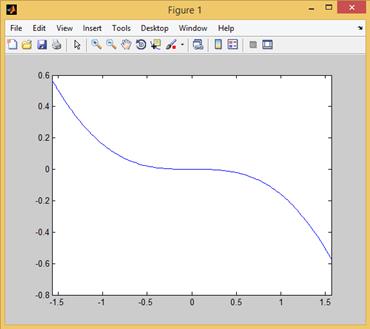
Рис. 2.20.1. График функции .

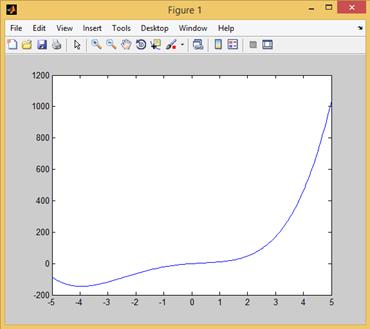
Рис. 2.21.1. График функции .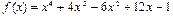

f =

Inline function:

f(x) = x(1)^2+x(2)^2

>> xmin=fminsearch(f,[1 1])

xmin =

1.0e-04 *

-0.2102 0.2548

Отметим, что для функции нескольких переменных большое значение (более существенное, чем для функции одной переменной) имеет предварительная оценка количества и приблизительного расположения локальных минимумов. Полезным здесь может оказаться опять-таки предварительное построение графика рассматриваемой функции.

Для получения сведений о количестве итераций, которое было сделано системой MATLAB для получения уточненного результата, необходимо обратиться к функции fminsearch следующим образом:

[xmin,val,flag,output]=fminsearch(hFun,x0)

где output – объект, содержащий полную информацию о процессе нахождения минимума функции. В частности, в поле output.iterations находится количество совершенных итераций. Для вывода соответствующего значения на экран следует использовать следующий синтаксис обращения:

>> [x,val,flag,output]=fminsearch(f,[1 1])

x =

1.0e-04 *

-0.2102 0.2548

val =

1.0915e-09

flag =

output =

iterations: 38

funcCount: 69

algorithm: 'Nelder-Mead simplex direct search'

message: 'Optimization terminated:

the current x satisfies the termination criteria using ...'

Численное интегрирование