Основные теоретические сведения.
Основные теоретические сведения о массивах были изложены в лабораторной работе №3. Данная лабораторная работа (№4) является логическим продолжением предыдущей и призвана закрепить навыки работы со статическими массивами на примере решения конкретных задач матричной алгебры.
Напомним основные моменты работы со статическими массивами.
1) Как и переменные, массивы необходимо объявлять. Запись double dArray[13][12] означает объявление двумерного массива dArray типа double размером 13×12 элементов, т.е. 13 строк и 12 столбцов.
2) Размер статических массивов определяется заранее и его нельзя менять. Если в задаче необходимо использовать массив переменного размера, то можно объявить массив заведомо большего размера и использовать в ходе решения только необходимую его часть. Например, в задаче требуется определить матрицу порядка n. Можно принять, что n <= 20 и объявить двумерный массив размером 20×20. Этого хватит для решения задачи для любого n <= 20.
3) Индексация в массивах начинается с нуля. Это означает, что для массива dArray индексы изменяются от 0 до 12 по строкам и от 0 до 11 по столбцам.
4) При работе с массивами широко используются циклы for. Следующий участок кода показывает пример обнуления двумерного массива dArray:
int i, j;
for ( i = 0; i < 13; i++ )
{
for ( j = 0; j < 12; j++ )
{
dArray[i][j] = 0;
}
}
5) Для инициализации больших массивов целесообразно использовать генератор случайных чисел.
Предположим, что по условию задачи массив dArray необходимо заполнить действительными числами, а затем определить количество положительных и отрицательных элементов массива. Примем следующее допущение: элементы массива будут иметь значения от –100 до +200. Тогда инициализацию массива можно провести следующим образом:
srand((unsigned)time(NULL));
int i, j;
for ( i = 0; i < 13; i++ )
{
for ( j = 0; j < 12; j++ )
{
dArray[i][j] = ( 300. * rand() / RAND_MAX ) - 100;
}
}
6) В ряде случаев условие задач может быть неполным и для решения целесообразно принимать дополнительные ограничения, например, задать диапазоны изменения входных данных и т.п.
Теперь вы обладаете достаточными знаниями для самостоятельного решения следующих задач.
Транспонирование матриц
Транспонированной называется матрица (АТ), в которой столбцы исходной матрицы (А) заменяются строками с соответствующими номерами.
Если А = (аij), то АТ = (аji).
Из определения следует, что если исходная матрица А имеет размер m × n, то транспонированная матрица АТ имеет размер n × m.
АЛГОРИТМ 3
Алгоритм операции транспонирования.
Исходные данные:
А[m×n] — исходная матрица.
Выходные данные:
M[n×m] — транспонированная матрица.
Вспомогательные переменные:
i, j — переменные для организации циклов.
Шаг 1. [Цикл по i]. Выполнить шаг 2 при i = 0,…,n – 1 и после этого завершить алгоритм.
Шаг 2. [Цикл по j]. Выполнить шаг 3 при j = 0,…,m – 1.
Шаг 3. [Установить М[i,j]]. М[i,j] = А[j,i]. (Формируем элементы транспонированной матрицы)
Сложение матриц
Складывать (вычитать) можно матрицы одного размера. Суммой матриц А = (аij) и В = (bij) размера m × n называется матрица С = А + В, элементы которой сij = aij + bij для i = 1,2,...,m; j = 1,2,…,n (т.е. матрицы складываются поэлементно).
АЛГОРИТМ 4
Алгоритм сложения двух матриц.
Исходные данные:
А[m×n], В[m×n] — исходные матрицы.
Выходные данные:
С[m×n] — результат суммирования.
Вспомогательные переменные:
i, j — переменные для организации циклов.
Шаг 1. [Цикл по i]. Выполнить шаг 2 при i = 0,…,m – 1 и после этого завершить алгоритм.
Шаг 2. [Цикл по j]. Выполнить шаг 3 при j = 0,…,n – 1.
Шаг 3. [Установить С[i,j]]. С[i,j] = А[i,j] + В[i,j].
Умножение матриц
Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй.
Пусть А = (аij) матрица размера m × n и В = (bij) матрица размера n × p, тогда размерность произведения А × В равна m × p. При этом матрица С (размера m × p) называется произведением матриц А и В, если каждый ее элемент равен сумме произведений элементов i–й строки матрицы А на соответствующие элементы j–го столбца матрицы В:
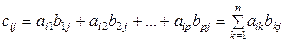
АЛГОРИТМ 5
Алгоритм умножения двух матриц.
Исходные данные:
А[m×n], В[n×p] — исходные матрицы.
Выходные данные:
С[m×p] — результат умножения.
Вспомогательные переменные:
i, j, k — переменные для организации циклов.
Шаг 1. [Цикл по i]. Выполнить шаг 2 при i = 0,…,m – 1 и после этого завершить алгоритм.
Шаг 2. [Цикл по j]. Выполнить шаги от 3 до 4 при j = 0,…,p – 1.
Шаг 3. [Установить С[i,j]]. С[i,j] = 0.
Шаг 4. [Цикл по k]. Выполнить шаг 5 при k = 0,…,n – 1.
Шаг 5. [Установить С[i,j]]. С[i,j] = С[i,j] + А[i,k] * В[k,j].
Задание на лабораторную работу №4
Задача 1. Разработать алгоритм и написать по нему программу транспонирования матрицы А размера m × n. Значение величин m и n выбрать из табл. 4.1 в соответствии с вариантом задания.
Задача 2. Разработать алгоритм и написать по нему программу сложения матриц А и В размера m × n. Значение величин m и n выбрать из табл. 4.1 в соответствии с вариантом задания.
Задача 3. Разработать алгоритм и написать по нему программу умножения матрицы А размера m × n на матрицу В размера n × p. Значение величин m, n, р выбрать из табл. 4.2 в соответствии с вариантом задания.
Оформить протокол лабораторной работы.
Примечание! Алгоритмы решения задач должны содержать не только расчетную часть, но и блоки формирования входных и выходных данных.
Варианты заданий
Таблица 4.1. Варианты заданий к задачам 1 и 2
| № | m, n | № | m, n | № | m, n |
| m = 2; n = 3 | m = 3; n = 5 | m = 5; n = 2 | |||
| m = 2; n = 4 | m = 3; n = 6 | m = 5; n = 3 | |||
| m = 2; n = 5 | m = 4; n = 2 | m = 5; n = 4 | |||
| m = 2; n = 6 | m = 4; n = 3 | m = 5; n = 5 | |||
| m = 3; n = 2 | m = 4; n = 4 | m = 5; n = 6 | |||
| m = 3; n = 3 | m = 4; n = 5 | m = 6; n = 2 | |||
| m = 3; n = 4 | m = 4; n = 6 |
Таблица 4.2. Варианты заданий к задаче 3
| № | m, n, p | m, n, p | |
| m = 2; n = 2; р = 2 | m = 4; n = 4; р = 4 | ||
| m = 3; n = 2; р = 2 | m = 5; n = 4; р = 4 | ||
| m = 4; n = 2; р = 2 | m = 2; n = 4; р = 5 | ||
| m = 5; n = 2; р = 2 | m = 3; n = 4; р = 5 | ||
| m = 2; n = 3; р = 3 | m = 4; n = 4; р = 5 | ||
| m = 3; n = 3; р = 3 | m = 5; n = 4; р = 5 | ||
| m = 4; n = 3; р = 3 | m = 2; n = 4; р = 6 | ||
| m = 5; n = 3; р = 3 | m = 3; n = 4; р = 6 | ||
| m = 2; n = 4; р = 4 | m = 4; n = 4; р = 6 | ||
| m = 3; n = 4; р = 4 | m = 5; n = 4; р = 6 |
Контрольные вопросы
Приведите алгоритм решения следующей задачи:
А = В * С + D
где A, B, C, D матрицы.
Какие следует принять дополнительные условия и ограничения для решения данной задачи?
Лабораторная работа №5
Цель: усовершенствовать навыки программирования на примере решения задач матричной алгебры с использованием динамических массивов.
Задачи:
1) Повторить теоретические сведения о создании и использовании диннамических массивов в языке Си++.
2) Разработать программу решающую одну из задач матричной алгебры.
