Оценка сложности основной процедуры – преобразование автомата
Министерство образования и науки Российской федерации
Государственное образовательное учреждение высшего профессионального образования «Донской государственный технический университет» ДГТУ
Кафедра «Программное обеспечение вычислительной техники и
автоматизированных систем»
Утверждаю
Зав. каф. «ПОВТ и АС»
________ Нейдорф Р.А.
«18» мая 2012 г.
Пояснительная записка
к курсовой работе
по дисциплине «Алгоритмические языки и программирование»
на тему «Машина Тьюринга»
Автор работы Бочаров Дмитрий Владимирович
Группа УСУ21
Специальность 230102 "Автоматизированные системы обработки информации и управления"
Руководитель работы ____________ Романенко Е.А.
(подпись)
Работа защищена «___»___________2012_ г. на оценку ______________
Члены комиссии ____________ __________________________
(подпись) (фамилия, инициалы)
____________ __________________________
(подпись) (фамилия, инициалы)
____________ __________________________
(подпись) (фамилия, инициалы)
г. Ростов-на-Дону
2012г.
Министерство образования и науки Российской федерации
Государственное образовательное учреждение высшего профессионального образования «Донской государственный технический университет» ДГТУ
Кафедра «Программное обеспечение вычислительной техники и
автоматизированных систем»
Утверждаю
Зав. каф. «ПОВТ и АС»
________ Нейдорф Р.А.
«18» мая 2012г.
задание
на курсовую работу
по дисциплине «Алгоритмы, построение и анализ»
Студент Бочаров Дмитрий Владимирович
Группа УСУ21
Тема работы: «Добавление и удаление элементов в красно-черном дереве»
Исходные данные: теоретические основы программирования на языке Pascal, лекции по дисциплине «Алгоритмы, построение и анализ»
Руководитель работы ____________ Романенко Е.А.
(подпись)
Задание принял к исполнению ____________ Бочаров Д.В.
(подпись)
Ростов–на–Дону
2012 год.
Постановка задачи
Машина Тьюринга представляет собой вариант конечного автомата,
обладающего свойством, обрабатывать символы ключа только от текущего к предыдущему или следующему символу ключа то есть для моделирования машины Тьюринга достаточно запрограммировать конечный автомат в соответствии со свойствами машины Тьюринга значит в программе надо задать такую таблицу переходов и выходов, чтоб данный конечный автомат можно было считать моделью машины Тьюринга.
Блок Схема Алгоритма
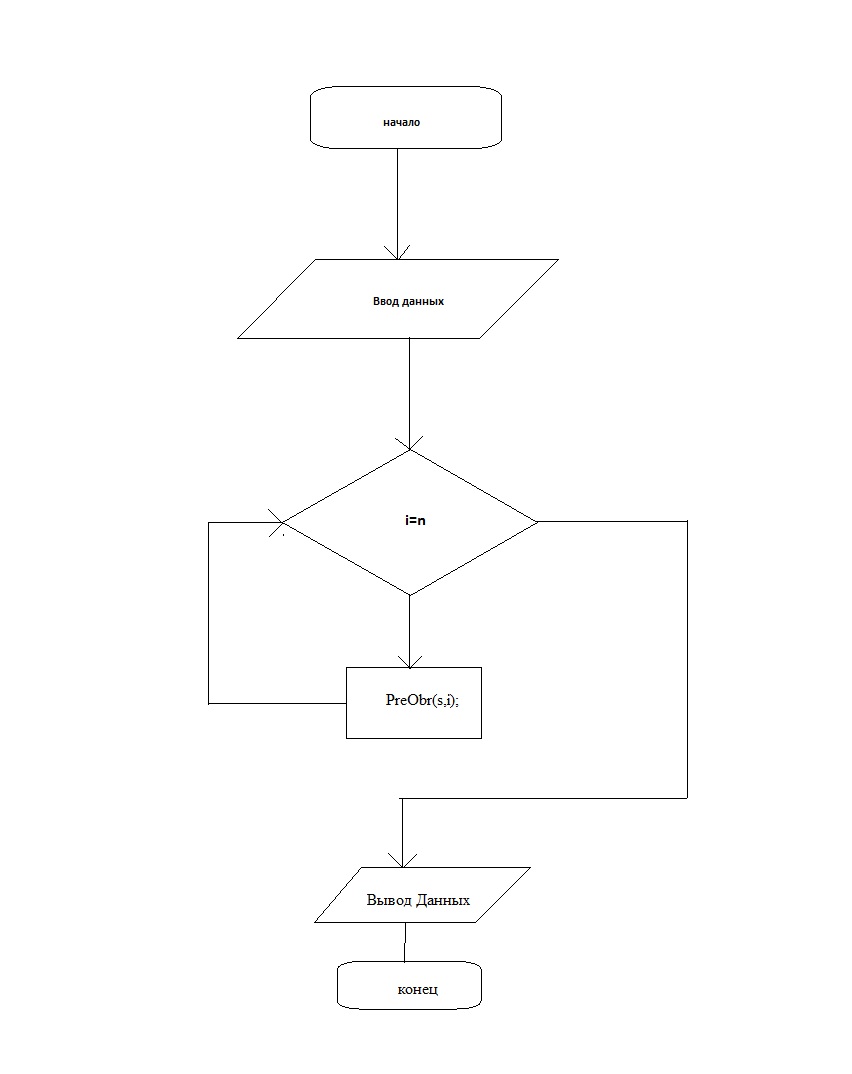
Листинг программы
ProgramMT; {Mashina Tiuringa}
usescrt;
Type
M=array[1..100] ofinteger;
Var
f,q:M; {Таблица переходов (f) и выходов (q)}
fi:integer;
ProcedurePreObr(vars:string; i:integer);
Begin
write(q[f[fi]]);
fi:=f[fi];
end;
Var
s:string;
l:integer; {Длина строки (кол-во введенных символов)}
{MaxState} Ms :integer; {Кол-во состояний исползуемых автоматом}
{MaxInSymbol} Mis:integer; {Кол-во входных символо, попадающих под обработку}
{MaxOutSymbol} Mos :integer; {Кол-во выходных символов, результат работы автомата}
{Таблица переходов (f) и выходов (q)}
i,j:integer;
x,y:shortint;
Begin
write('Введите кол-во используемых состояний автомата: ');
x:=whereX;
y:=whereY;
repeat{Проверка ввода кол-ва состояний, должно быть >0}
readln(Ms);
ifMs > 0 then break;
gotoXY(x,y);
untilfalse;
write('Введите символьную последовательность: ');
readln(s);
l:=length(s); // Кол-во семволов строке- количество итераций автомата.
Writeln('Запилните таблицы f и q : ');
Writeln('{f}');
{Таблица переходов и одного состояния в другое, в ней
указуются номера состояний в которые будет переходить автомат
после очередного выполнения преобразования, начинает работу с выполнения состояния на которое переходит из начального}
fori:=1 toMs do
write('---');
writeln;
write('Ms: ');
fori:=1 toMs do
write('| ',i);
writeln('|');
fori:=1 toMs do
write('---');
writeln;
write('fi: '); {Переход на следующее состояние автомата}
{Таблица преобразования,в нейзадается задается
(в данной программе) чем замениться текущий символ подлежащий обработке.}
fori:=1 toMs do
Begin
write('|');
x:=whereX;
y:=whereY;
readln(f[i]);
gotoXY((x+2),y);
end;
writeln('|');
Writeln('{q}');
fori:=1 toMs do
write('---');
writeln;
write('Ms: ');
fori:=1 toMs do
write('| ',i);
writeln('|');
fori:=1 toMs do
write('---');
writeln;
write('qO: '); {qO это выходное значение qOut}
fori:=1 toMs do
Begin
write('|');
x:=whereX;
y:=whereY;
readln(q[i]);
gotoXY((x+2),y);
end;
writeln('|');
Write('Введите ключ, задайте начальное состояние: ');
readln(fi);
{Начальное состояние, можно задавать с клавиатуры.}
Write('Результат работы: ');
fori:=1 tol do
PreObr(s,i);
Writeln;
Writeln(' Press Enter...');
readln;
end.
Оценка сложности основной процедуры – преобразование автомата
Оценка сложности процедуры PreObr:
| l:=length(s) | C1 | |
| for i:=1 to l do | C2 | N |
| begin | ||
| write(q[f[fi]])); | C3 | N |
| fi:=f[fi]; | C4 | N |
| end; | C5 |
T(преобразование автомата)=c1*1+c2*N+c3*N+c4*N+c5*1= (с1+c5) +N*(c2+c3+c4)= N, где единичные операции, в малых не больших количествах, пренебрежительно малы в сравнении с N Общая сложность = Q(n).
Рекомендации пользователю
1. После запуска программы выводится общее окно работы с машиной Тьюринга.
2. Указать кол-во Вершин.
3. Заполнить массивы F и Q.
4. Задать начальное положение автомата.
5. Вывод результата.
Пример работы программы
Вот пример для замены двух крайних значений местами
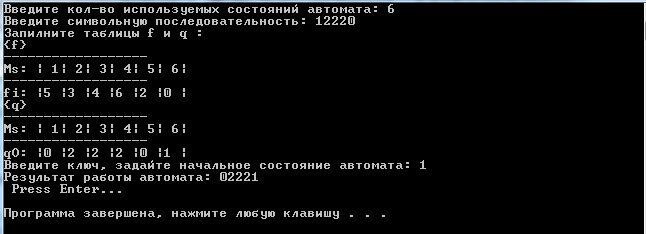
Начальное состояние 1, значит автомат начинает работу и переходит в состояние 5 , затем по таблиец q смотрит на каким символом надо заменить первый символ «символьной последовательности», и заменяет его на «0», что соответствует столбику 5 в таблице q.
За тем выполнив состояние 5 он переходит по таблице f в состояние 2, и заменяет второй, т е следующий (в соответсвие свойству машины Тьбринга – соседний элемент) символ на символ, «2», судя по таблице q, где во втором столбике написана двойка, и так до последнего элемента,
а когда при обработке последнего символа из состояния 4 переходят в состояние 6 и заменяют последний символ «0» из исходной последовательности на символ «1» в соответствии с текущем состоянием в таблице f и значением соответствующим шестому столбцу в таблице q.
Это пример работы программы и использования машины Тьюринга.
Заключение
Машина Тьюринга - это очень простое вычислительное устройство. Она состоит из ленты бесконечной длины, разделенной на ячейки, и головки, которая перемещается вдоль ленты и способна читать и записывать символы. Также у машины Тьюринга есть такая характеристика, как состояние, которое может выражаться целым числом от нуля до некоторой максимальной величины. В зависимости от состояния машина Тьюринга может выполнить одно из трех действий: записать символ в ячейку, передвинуться на одну ячейку вправо или влево и установить внутреннее состояние.
Устройство машины Тьюринга чрезвычайно просто, однако на ней можно выполнить практически любую программу. Для выполнения всех этих действий предусмотрена специальная таблица правил, в которой прописано, что нужно делать при различных комбинациях текущих состояний и символов, прочитанных с ленты.
В результате проделанной работы мы получили программу,реализующую алгоритм Машины Тьюринга.
Список использованной литературы
1. Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман Глава 8. Введение в теорию машин Тьюринга // Введение в теорию автоматов, языков и вычислений = Introduction to Automata Theory, Languages, and Computation. — М.: «Вильямс», 2002. — С. 528. —
2. http://ru.wikipedia.org/wiki/Машина_Тьюринга
3. Алгоритмы и структуры данных 2008 г. Никлаус Вирт
4. Т. Кормен, Ч. Лейзерсон, Р. Ривест. Алгоритмы: построение и анализ. МЦНМО, Москва, 2001
