Сортировка посредством выбора

Еще одно важное семейство методов сортировки основано на идее многократного выбора. Вероятно, простейшая сортировка посредством выбора сводится к следующему.

1. Найти наименьший ключ, переслать соответствующую запись в область вывода и заменить ключ значением ¥, которое по предположению больше любого реального ключа;

2. Повторить шаг (1). На этот раз будет выбран ключ, наименьший из оставшихся, так как ранее наименьший ключ был заменен значением ¥;

3. Повторять шаг (1) до тех пор, пока не будут выбраны N записей.

Данный метод называется сортировка путем простого выбора. Заметим, что этот метод требует наличия всех исходных элементов до начала сортировки, а элементы вывода порождает последовательно, один за другим. Картина по существу, противоположна картине, возникающей при использовании метода вставок, в котором исходные записи поступают последовательно, но вплоть до завершения сортировки об окончательном результате ничего неизвестно.

Пирамидальная сортировка [17]

Назовем пирамидой (heap) бинарное дерево высоты k, в котором

• все узлы имеют глубину k или k-1.
• уровень k-1 дерева полностью заполнен, а уровень k заполнен слева направо

• выполняется "свойство пирамиды": каждый элемент меньше, либо равен родителю.

Ниже на рисунке 27 показано дерево, удовлетворяющее свойству пирамиды

Рис. 27. Пример дерева, удовлетворяющего свойству пирамиды

Для хранения пирамиды можно использовать массив. В a[0] хранится корень дерева; левый и правый потомки элемента a[i] хранятся в a[2i+1] и a[2i+2] соответственно.

Фаза 1: построение пирамиды

Построение пирамиды начинается с a[k]...a[n], k = [size/2]. Эта часть массива уже удовлетворяет свойству пирамиды.

Далее необходимо расширять данную часть массива, добавляя по одному элементу за шаг. Для этого необходимо просмотреть правого и левого потомков - в массиве это a[2i+1] и a[2i+2] и выбрать наибольшего из них.

Если этот элемент больше a[i], то необходимо поменять его с a[i] местами. Таким образом новый элемент "просеивается" сквозь пирамиду.

Фаза 2: сортировка

1. Необходимо взять верхний элемент пирамиды a[0]...a[n] (первый в массиве) и поменять с последним местами. Далее этот элемент из рассмотрения необходимо исключить, так как он уже занял нужное место в массиве. Рассматривается массив a[0]...a[n-1]. Для превращения его в пирамиду достаточно просеять лишь новый первый элемент описанным выше способом.

2. Необходимо повторять шаг 1, пока обрабатываемая часть массива не уменьшится до одного элемента.

Очевидно, что в конец массива каждый раз будет попадать максимальный элемент из текущей пирамиды, поэтому в правой части постепенно возникает упорядоченная последовательность.

Вторая фаза занимает O(n log n) операций. К положительным сторонам данного способа сортировки относится тот факт, что пирамидальная сортировка не использует дополнительной памяти.

Сортировка методом слияния [18]

Слияние означает объединение двух или более упорядоченных массивов в один упорядоченный массив. Можно, например, слить подмассивы 503 703 765 и 087 512 677 и получить 087 503 512 677 703 765. Простой способ сделать это - сравнить два наименьших элемента, вывести наименьший из них и повторить эту процедуру.

Начав с

получим

затем

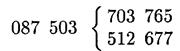
и

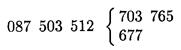
и т. д. пока не исчерпается хотя бы один подмассив. Если это произойдет, то в результирующий массив необходимо добавить все оставшиеся члены другого подмассива.

Задачу сортировки можно свести к слиянию, сливая все более длинные подмассивы до тех пор, пока не будет рассортирован весь массив. Такой подход можно рассматривать как развитие идеи сортировок методом вставок: вставка нового элемента в упорядоченный массив – это частный случай слияния при n=1. Чтобы ускорить процесс вставок, можно рассмотреть вставку нескольких элементов за один раз, группируя несколько операций, а это естественным образом приведет к общей идее сортировки методом слияния.

На рисунке 28 проиллюстрирована сортировка методом слияния, когда возрастающие серии выделяются как с начала массива, так и с его конца.

Рис. 28. Сортировка методом естественного двухпутевого слияния

Вертикальными линиями на рисунке 28 отмечены границы между сериями. Сложность данного алгоритма составляет O(n log n) операций.

Основной сложностью практической реализации данного алгоритма является необходимость создания дополнительных массивов для хранения результатов, либо большой объем по перемещению данных внутри одного массива. Поэтому, наиболее оптимальной структурой данных для данного алгоритма являются односвязные списки, с помощью которых удастся избежать излишнего расхода памяти в случае временных массивов, а также перемещения данных внутри них.