Силовой расчет силовой судовой установки
РЕФЕРАТ
В курсовом проекте выполнено проектирование одноцилиндрового нереверсивного двухтактного двигателя судовой силовой установки.
Проведено:
· определения закона установившегося движения;
· силовой расчет механизма судовой силовой установки;
· проектирование прямозубой цилиндрической зубчатой передачи;
· проектирование планетарного реверс-редуктора для хода назад;
· проектирование кулачкового механизма плунжерного топливного насоса.
Расчетно-пояснительная записка содержит 68 листа формата А4; 6 таблиц; курсовой проект выполнен на 4 листах формата А1
СОДЕРЖАНИЕ
РЕФЕРАТ 1
СОДЕРЖАНИЕ 2
ТЕХНИЧЕСКОЕ ЗАДАНИЕ 4
Назначение, функциональная схема, принцип работы 4
Схема установки 5
Исходные данные 5
1. ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ СИЛОВОЙ СУДОВОЙ УСТАНОВКИ 7
1.1 Определение размеров звеньев силовой судовой установки 7
1.2 Построение индикаторной диаграммы и диаграммы сил, действующих на поршни 8
1.2.1 Построение индикаторной диаграммы. 8
1.2.2 Построение диаграммы сил. 8
1.3 Определение значений передаточных функций и передаточных отношений основного механизма 9
1.4 Расчет одномассовой динамической модели 9
1.4.1 Определение суммарного приведенного момента внешних сил, приложенных к звеньям механизма 9
1.4.2 Определение приведенных моментов инерции звеньев механизма 11
1.5 Определение суммарной работы приведенного момента движущих сил и сил сопротивления 12
1.5.1 Построение графика работы движущих сил 12
1.5.2 Построение графика суммарной работы 13
1.6 Определение кинетической энергии первой и второй групп звеньев механизма 13
1.6.1 Построение приближенных графиков кинетической энергии второй группы звеньев 13
1.6.2 Построение графика кинетической энергии первой группы звеньев 13
1.7 Определение момента инерции первой группы звеньев 14
1.8 Определение момента инерции, габаритных размеров и массы маховика. 14
1.9 Определение закона движения механизма 15
2. СИЛОВОЙ РАСЧЕТ СИЛОВОЙ СУДОВОЙ УСТАНОВКИ 16
2.1 Исходные данные для силового расчета 16
2.2 Построение планов скоростей и ускорений 17
2.2.1 Построение планов скоростей 17
2.2.2 Построение планов ускорений 19
2.3 Расчет нагрузок, приложенных к механизму 21
2.4 Определение реакций в кинематических парах 21
2.4.1 Расчет группы звеньев 2-3 21
2.4.2 Расчет группы звеньев 4-6 22
2.4.3 Расчет звена 1 23
3. ПРОЕКТИРОВАНИЕ ЗУБЧАТОЙ ПЕРЕДАЧИ И ПЛАНЕТАРНОГО МЕХАНИЗМА РЕВЕРC-РЕДУКТОРА СИЛОВОЙ СУДОВОЙ УСТАНОВКИ 25
3.1 Исходные данные 25
3.2 Проектирование зубчатой передачи 25
3.2.1 Расчет параметров исходного производящего контура 25
3.2.2 Расчет параметров зубчатых колес 26
3.2.3 Построение профиля зуба колеса, изготавливаемого реечным инструментом 27
3.2.4 Построение проектируемой зубчатой передачи. 29
3.3 Проектирование планетарного механизма реверс-редуктора 30
4. ПРОЕКТИРОВАНИЕ КУЛАЧКОВОГО МЕХАНИЗМА ПЛУНЖЕРНОГО ТОПЛИВНОГО НАСОСА 33
4.1 Исходные данные 33
4.2 Построение кинематических диаграмм 33
4.3 Определение основных параметров кулачкового механизма графическим способом 34
4.4 Построение профиля кулачка 34
4.5 Построение диаграммы изменения угла давления 34
5. ЗАКЛЮЧЕНИЕ 35
СПИСОК ЛИТЕРАТУРЫ 36
ПРИЛОЖЕНИЕ 1 37
П1.1 Листинг 1 37
ПРИЛОЖЕНИЕ 2 57
П2.1 Листинг 1 57
ПРИЛОЖЕНИЕ 3 65
П3.1 Листинг 1 65
ПРИЛОЖЕНИЕ 4 72
П4.1 Листинг 1 72
ТЕХНИЧЕСКОЕ ЗАДАНИЕ
Назначение, функциональная схема, принцип работы
Задание ОПМ-48Б. Проектирование и исследование механизмов судовой силовой установки.
Судовая силовая установка состоит из одноцилиндрового нереверсивного двухтактного двигателя внутреннего сгорания с двумя расходящимися поршнями (1, 2, 3, 4-4”, 5-5”, 6) с воспламенением от сжатия, маховика 7, планетарного реверс-редуктора 8, однорядного редуктора 9, гребного вала с винтом 10.
Вал двигателя 1 имеет три колена. Среднее колено ОА через шатун АВ 2 сообщает движение нижнему поршню 3, а крайние два колена ОС и ОС”, расположенные под углом 180 градусов к среднему, сообщает через шатуны 5-5” движение верхнему поршню 6 в сторону, противоположенную движения поршня 3. В процессе работы двигателя поршни 3 и 6 то расходятся, то сближаются. Наименьшее расстояние между поршнями определяется по заданной геометрической степени сжатия 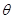 как отношение наибольшего к наименьшему расстоянию между поршнями
как отношение наибольшего к наименьшему расстоянию между поршнями
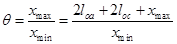
От коленчатого вала 1 движение передается гребному валу через планетарный редуктор 8 (водило, Z1, Z2, Z3, Z4) с фрикционными муфтами L и M и через одноступенчатый редуктор 9 с цилиндрическими прямозубыми колёсами.
Для движения судна вперед включается фрикционная муфта L, связывающая колёса Z1 и Z4, вследствие чего водило и колеса Z1, Z2, Z3, Z4 вращаются как одно целое относительно геометрических осей колеса Z1 и водила. Для движения судна назад включается муфта М и отключается муфта L. При этом колесо Z4 останавливается, а колесо Z1 получает вращение в обратную сторону. Для остановки судна обе муфты отключаются.
Закон изменения давления газа в цилиндре двигателя при перемещении поршней представлен индикаторной диаграммой, а данные для её построения приведены в таблице 2.
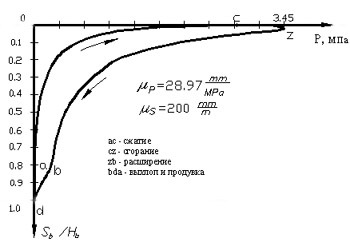
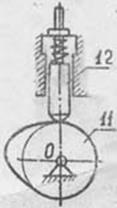
В двухтактном двигателя такого типа при расхождении поршней в цилиндре происходит сгорание впрыснутого топлива и расширение продуктов сгорания, а при сближении их - сжатие воздуха, нужного для сгорания. Схема кулачкового механизма топливного плунжерного насоса изображена на рисунке. Кулачок 11 этого механизма посажен непосредственно на коленчатый вал двигателя. Закон движения плунжера 12 насоса задан графиком ускорений
Схема установки
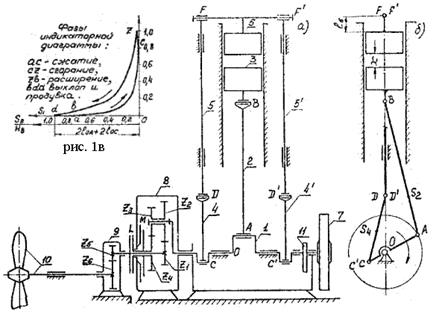 рис. 1а рис. 1б рис. 1а рис. 1б | 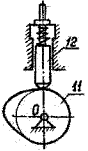 рис. 1г рис. 1г |
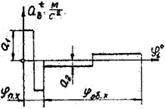 рис. 1д рис. 1д |
Исходные данные
Таблица 1.
| №пп | Параметр | Обозначение | Размерность | Значение |
| Средняя скорость поршня | (VB)ср | м/с | ||
| Число оборотов коленчатого вала | n1 | 1/c | 25/6 | |
| Число оборотов гребного вала | n10 | 1/c | 125/60 | |
| Отношение длин шатунов к длинам кривошипов | lВА/lOA; lCD/lOC | - | ||
| Отношение хода поршня 6 к ходу поршня 3 | HD/HB | - | 0.4 | |
| Отношение, определяющие положения центров тяжести шатунов | lAS2/lAB; lсs4/lCD | - | 1/3 | |
| Масса коленчатого вала с маховиком | m1+ mмах | кг | ||
| Масса шатуна АВ | m2 | кг | ||
| Масса шатуна CD | m4 | кг | ||
| Масса нижнего поршня 3 | m3 | кг | ||
| Масса верхнего поршня 6 | m6 | кг | ||
| Масса тяги DE(D’E’) | m5, m5’ | кг | ||
| Момент инерции коленчатого вала без маховика | J’O1 | кг*м2 | ||
| Момент инерции шатуна AB | JS2 | кг*м2 | ||
| Момент инерции шатуна CD(C’D’) | JS4 | кг*м2 | ||
| Момент инерции движущихся частей реверс-редуктора, приведенный к валу кривошипа | Jпрр.р. | кг*м2 | ||
| Маховый момент гребного вала с винтом | Jвинта | кг*м2 | ||
| Диаметр цилиндра | d | м | 0,4 | |
| Максимальное давление в цилиндре | pmax | Па | 5.5*106 | |
| Геометрическая степень сжатия, где х - расстояние между поршнями | θ=хmax/хmin | - | ||
| Коэффициент неравномерности вращения коленчатого вала | δ | - | 1/45 | |
| Угловая координата кривошипа для силового расчета | φ1 | град | ||
| Число зубьев колеса Z5 | Z5 | - | ||
| Модуль колес Z5, Z6 | m56 | мм | ||
| Наименьший радиус кулачка, определяемый прочностью вала | R0 | м | 0,08 | |
| Число сателлитов планетарной передачи | k | - | ||
| Полное перемещение плунжера топливного насоса | h | м | 0,025 | |
| Модуль зубчатых колес планетарного реверса | mп.р. | мм | ||
| Угол рабочего профиля кулачка | φраб | град | ||
| Максимально допустимый угол давления кулачка | [θ] | град |
Таблица 2.
Значения давления в цилиндре двигателя (в долях pmax) в зависимости от положения поршней.
| Координаты поршней в долях от Н | SB/HB | 0.02 | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| При расхождение поршней | p/pmax | 0.863 | 1.000 | 0.863 | 0.602 | 0.34 | 0.238 | 0.170 | 0.129 | 0.100 | 0.082 | 0.068 | 0.034 | |
| При сближение поршней | p/pmax | 0.863 | 0.5 | 0.318 | 0.204 | 0.114 | 0.073 | 0.045 | 0.025 | 0.014 | 0.005 | 0.001 |
1. ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ СИЛОВОЙ СУДОВОЙ УСТАНОВКИ
1.1 Определение размеров звеньев силовой судовой установки
Проектирование кривошипно-ползунного механизма ведется по средней скорости поршня (ползуна). При этом известными являются следующие параметры:
средняя скорость поршня: υср=5 м/с,
частота вращения вала кривошипа: n1=25/6 c-1.
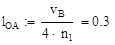
где lOA – длина кривошипа ОА, м.
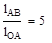
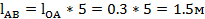
где lAB– длина шатуна АВ, м.
HD=2*lOC
HB=2*lOA
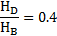
lOC=0.4*lOA=0.12м
где lОС – длина кривошипа ОС, м,
HBи HD– ходы поршней 3 и 6 соответственно, м.
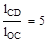
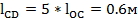
где lCD– длина шатуна CD, м.
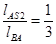
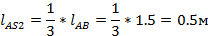
где lAS2– расстояние от точки А до положения центра тяжести звена 2 – точки S2, м.
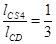
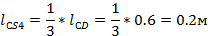
где lCS42– расстояние от точки Cдо положения центра тяжести звена 3 – точки S4, м.
1.2. Построение индикаторной диаграммы и диаграммы сил, действующих на поршни
1.2.1 Построение индикаторной диаграммы.
Справа от точки B построена индикаторная диаграмма на ходе поршня 3. От нулевого положения механизма вниз отложена ось SB/HB, которая поделена на 10 равных частей. Вправо отложена ось давлений. По данным из таблицы №2 построена индикаторная диаграмма.
Масштабы индикаторной диаграммы, μp:
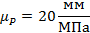
Все расчеты проведены при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
1.2.2 Построение диаграммы сил.
Если давление Р, Па при любом положение поршня помножить на его площадь, S, то получится сила давления газов на поршень, то есть сила 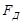 .
.
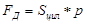
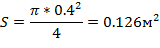
Оси координат диаграммы сил расположены аналогично осям индикаторной диаграммы. Положительное направление оси SВ – вниз, положительное направление оси 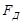 - вправо. На диаграммы сил перенесены ординаты с индикаторной диаграммы с учётом знака силы.
- вправо. На диаграммы сил перенесены ординаты с индикаторной диаграммы с учётом знака силы.
Масштабы диаграммы сил:
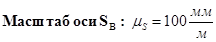
Масштаб оси Fд : 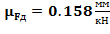
Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
1.3. Определение значений передаточных функций и передаточных отношений основного механизма
Определение значение передаточных функций основного механизма, произведено с помощью программы Mathcad.
Результаты вычислений представлены в таблице 3.
Таблица 3
| VqB, м | -0,176 | -0,286 | -0,3 | -0,233 | -0,124 | 0,124 | 0,233 | 0,3 | 0,286 | 0,176 | |||
| VqS2,м | 0,2 | 0,235 | 0,287 | 0,3 | 0,27 | 0,224 | 0,2 | 0,224 | 0,27 | 0,3 | 0,287 | 0,235 | 0,2 |
| VqF, м | 0,05 | 0,093 | 0,12 | 0,114 | 0,07 | -0,07 | -0,114 | -0,12 | -0,093 | -0,05 | |||
| VqS4,м | 0,08 | 0,089 | 0,108 | 0,12 | 0,115 | 0,094 | 0,08 | 0,094 | 0,115 | 0,12 | 0,108 | 0,089 | 0,08 |
Все расчеты проведены при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
1.4 Расчет одномассовой динамической модели
Для механизма с одной степенью свободы достаточно определить закон движения одного звена, а законы движения остальных звеньев всегда можно определить с помощью кинематических методов. Заменим механизм одномассовой динамической моделью механизма.
1.4.1 Определение суммарного приведенного момента внешних сил, приложенных
к звеньям механизма
Приведенный момент сил 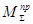 - расчетный момент пары сил, определяемый из равенства его элементарной работы сумме элементарных работ сил и пар сил, приложенных к звеньям механизма.
- расчетный момент пары сил, определяемый из равенства его элементарной работы сумме элементарных работ сил и пар сил, приложенных к звеньям механизма.
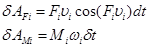
где 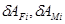 - элементарные работы силы на элементарном перемещении точки ее приложения и момента пары сил на элементарном угле поворота звена соответственно;
- элементарные работы силы на элементарном перемещении точки ее приложения и момента пары сил на элементарном угле поворота звена соответственно;
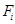 - сила
- сила
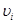 - скорость точки ее приложения
- скорость точки ее приложения
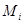 - момент пары сил
- момент пары сил
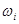 - угловая скорость звена
- угловая скорость звена
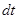 - элементарный промежуток времени
- элементарный промежуток времени
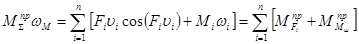
где
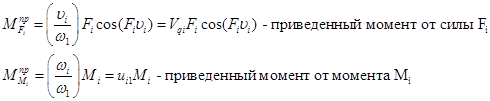
Vqi – передаточная функция для i-ой точки,
ui1 – передаточное отношение i-го звена, по отношению к звену 1.
Значения передаточных функций определены аналитическим способом в п.2.3.
Значения приведенных моментов сил тяжести, MпрGi, найдены как произведение сил тяжести на проекции передаточных функций (выражены в аналитической форме) на ось абсцисс:
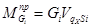
Значение приведенного момента движущей силы 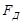 найдены:
найдены:
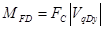
Определим движущий момент из условия равенства работ сил сопротивления и движущих сил за цикл (установившийся режим движения механизма):
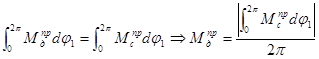 , так как мы считаем движущий момент постоянным.
, так как мы считаем движущий момент постоянным.
Масштабы графика приведенных моментов:
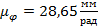
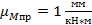
Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1. По этим данным построен график изменения приведенного момента сил 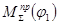 .
.
1.4.2 Определение приведенных моментов инерции звеньев механизма
Приведенный момент инерции 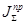 - расчетный момент инерции динамической модели, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма. То есть приведенный момент инерции можно определить из равенства кинетических энергий:
- расчетный момент инерции динамической модели, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма. То есть приведенный момент инерции можно определить из равенства кинетических энергий:
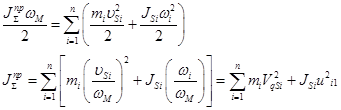
где JпрΣ– суммарный приведенный момент инерции,
ωм – угловая скорость модели,
mi – масса i-го звена,
VqSi – передаточная функция i-ой точки,
ISi – момент инерции i-го звена,
ui1 – передаточное отношение i-го звена, по отношению к звену 1.
Звенья механизма разделены на две группы. В первую входят те звенья, для которых приведенный момент является постоянной величиной. Это звенья, которые совершают только вращательное движение, их приведенный суммарный момент инерции обозначаются: 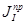 .
.
Ко второй группе относятся звенья, для которых приведенный момент инерции не является постоянной величиной. Эти звенья совершают плоское, возвратно-вращательное и возвратно-поступательное движения. Их приведенный суммарный момент инерции обозначаются 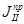 .
.
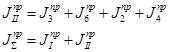
где Jпрi – приведенный момент инерции i-го звена.
Числовые значения составляющих 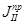 , рассчитаны при помощи программы Mathcad, результаты расчетов приведены в Приложении 1. На чертеже представлены графики изменения приведенного момента инерции второй группы звеньев механизма,
, рассчитаны при помощи программы Mathcad, результаты расчетов приведены в Приложении 1. На чертеже представлены графики изменения приведенного момента инерции второй группы звеньев механизма, 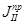 , и его составляющих
, и его составляющих 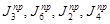 .
.
Масштабы графика суммарного приведенного момента инерции:

1.5. Определение суммарной работы приведенного момента движущих сил и сил сопротивления
1.5.1 Построение графика работы движущих сил
Имея график 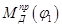 можно получить график
можно получить график 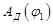 работы суммарного приведенного момента движущих сил, приложенных к механизму путем графического интегрирования.
работы суммарного приведенного момента движущих сил, приложенных к механизму путем графического интегрирования.
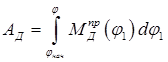
Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1. По этим данным построен график работы момента движущих сил 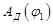 .
.
Масштабы графика работы:

1.5.2 Построение графика суммарной работы
При установившемся движении механизма, суммарная работа АΣ за цикл равна нулю.
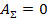
Значит, работа сил сопротивления за цикл Асц численно равна работе сил движущих за цикл АДц.
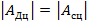
В предположении, что приведенный момент движущих сил постоянный Мпрд=const, построен график работы сил сопротивления. Методом графического интегрирования было определено значение Мпрд.
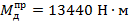
График суммарной работы АΣ(φ1) построен, как алгебраическая сумма графиков AД(φ1) и Ас(φ1).
Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
1.6 Определение кинетической энергии первой и второй групп звеньев механизма
1.6.1 Построение приближенных графиков кинетической энергии второй группы звеньев
Кинетическая энергия второй группы звеньев 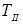 определена через приведенные моменты инерции этой же группы звеньев.
определена через приведенные моменты инерции этой же группы звеньев.
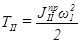
Закон изменения 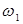 еще неизвестен. Поэтому для определения
еще неизвестен. Поэтому для определения 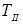 воспользуемся приближенным равенством
воспользуемся приближенным равенством 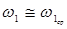 , поскольку коэффициент неравномерности
, поскольку коэффициент неравномерности 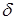 - величина малая.
- величина малая.
Тогда
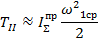
где ω1ср – средняя угловая скорость звена 1.
Так как 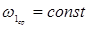 , то
, то 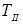 можно считать пропорциональной
можно считать пропорциональной 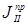 , а построенную кривую
, а построенную кривую 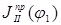 принять за приближенную кривую
принять за приближенную кривую 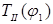 .
.
Масштаб графика 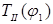 :
:

Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
1.6.2 Построение графика кинетической энергии первой группы звеньев
Для построения кривой кинетической энергии первой группы звеньев TI(φ1) необходимо из ординат кривой 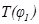 в каждом положении механизма вычесть отрезки, изображающие величины TII, взятые из графика TII(φ1). Вычитаемые отрезка должны быть представлены обязательно в том же масштабе
в каждом положении механизма вычесть отрезки, изображающие величины TII, взятые из графика TII(φ1). Вычитаемые отрезка должны быть представлены обязательно в том же масштабе 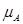 , в каком построена кривая
, в каком построена кривая 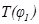 . Полученная кривая TI(φ1) - приближенная, так как построена вычитанием из точной кривой
. Полученная кривая TI(φ1) - приближенная, так как построена вычитанием из точной кривой 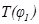 приближенных значений
приближенных значений 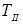 .
.
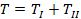
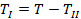
где Т – полная кинетическая энергия системы,
ТI – кинетическая энергия первой группы звеньев,
ТII – кинетическая энергия второй группы звеньев.
Так как полная кинетическая энергия системы – это сумма начальной кинетической энергии и суммарной работы, то графиком T (φ1) будет являться график АΣ(φ1) относительно оси φ*1. Поэтому, для построения графика TI (φ1), были вычтены соответствующие значения TII(φ1) из графика АΣ(φ1).
1.7 Определение момента инерции первой группы звеньев
Момент инерции первой группы звеньев JпрI рассчитан по формуле
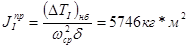
где JпрI – приведенный момент инерции первой группы звеньев,
(ΔTI)max = TImax - TImin – максимальное изменение кинетической энергии первой группы звеньев, определяемое из графика TI (φ1), как разность между максимальным, TImax и минимальным, TImin значениями кинетической энергии первой группы звеньев за цикл.
Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
1.8 Определение момента инерции, габаритных размеров и массы маховика.
В первую группу звеньев входят вал двигателя, планетарный реверс-редуктор, гребной вал с винтом. Все эти звенья, связанные с начальным звеном постоянным передаточным отношением, обладают маховыми массами, которые влияют на закон движения начального звена.
Момент инерции маховика определен, как разность между приведенным моментом инерции первой группы звеньев и моментами инерции звеньев, связанных с начальным звеном.
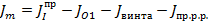
где Jm – момент инерции маховика,
JO1 – момент инерции коленчатого вала двигателя без маховика,
Jвинта – момент инерции гребного вала с винтом,
Jпр.р.р. – приведенный момент инерции движущихся частей реверс-редуктора.
Расчеты габаритных размеров и массы маховика проведены для диска.
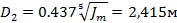
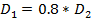
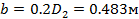
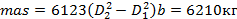
где D2 ,D1– наружный и внутренний диаметр маховика,соответственно,
b – ширина маховика,
mas – масса маховика.
Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
1.9 Определение закона движения механизма
Графиком ω1(φ1) является кривая TI относительно оси φ**1. Для определения положения этой оси была рассчитана ордината среднего значения угловой скорости.
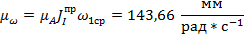
где μω – масштаб угловой скорости первого звена.
Через середину отрезка (ω1max-ω1min) , была проведена прямая ω1ср =const.
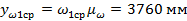
где yω1ср – ордината среднего значения угловой скорости первого звена.
Из полученного графика ω1(φ1) была определена начальная угловая скорость первого звена ω1нач. Начальная кинетическая энергия Тнач была определена по формуле
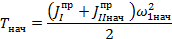
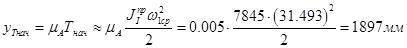
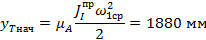
Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 1.
СИЛОВОЙ РАСЧЕТ СИЛОВОЙ СУДОВОЙ УСТАНОВКИ
