Классификация методов представления знаний

Для того чтобы манипулировать всевозможными знаниями из реального мира с помощью компьютера, необходимо осуществить их моделирование.

При проектировании модели представления знаний следует учесть два требования: однородность представления; простоту понимания.

Выполнение этих требований позволяет упростить механизм логического вывода и процессы приобретения знаний и управления ими, однако, как правило, создателям интеллектуальной системы приходится идти на некоторый компромисс в стремлении обеспечить одинаковое понимание знаний и экспертами, и инженерами знаний, и пользователями.

Классификация методов моделирования знаний с точки зрения подхода к их представлению в ЭВМ показана на рис. 13.1.

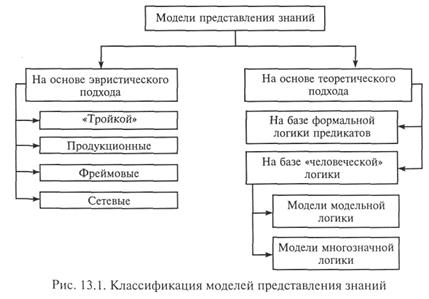
Дадим общую характеристику основных методов представления знаний.

Модели на основе эвристического подхода.Представление знаний тройкой «объект — атрибут — значение». Один из первых методов моделирования знаний. Как правило, используется для представления фактических знаний в простейших системах.

Примеры.

Очевидно, что для моделирования знаний даже об одном объекте (например, о «студенте» или «доме») из предметной области необходимо хранить значительное число «троек».

Продукционная модель. Модель правил; модель продукций — от англ. production — изготовление, выработка. В настоящее время наиболее проработанная и распространенная модель представления знаний, в частности в ЭС.

Модель предусматривает разработку системы продукционных правил (правил продукций), имеющих вид:

ЕСЛИ А₁И А₂ И ... И А_n, ТО B₁ИЛИ В₂ИЛИ ... ИЛИ В_т,

где А_i и B_j — некоторые высказывания, к которым применены логические операции И и ИЛИ. Если высказывания в левой части правила (ее часто называют антецедент — условие, причина) истинно, истинно и высказывание в правой части (консеквент — следствие).

Полнота базы знаний (базы правил) определяет возможности системы по удовлетворению потребностей пользователей. Логический вывод в продукционных системах основан на построении прямой и обратной цепочек заключений, образуемых в результате последовательного просмотра левых и правых частей соответствующих правил, вплоть до получения окончательного заключения.

Пусть в некоторой области памяти (базе знаний) хранятся следующие правила (суждения):

· правило 1: ЕСЛИ в стране происходит падение курса национальной валюты, ТО материальное положение населения ухудшается;

· правило 2: ЕСЛИ объемы производства в стране падают, ТО курс национальной валюты снижается;

· правило 3: ЕСЛИ материальное положение населения ухудшается, ТО уровень смертности в стране возрастает.

Если на вход системы поступит новый факт (факт 1) «В стране высокий уровень падения объемов производства», то из правил можно построить цепочку рассуждений и сформулировать два заключения:

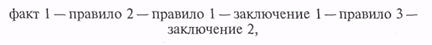
где заключение 1 (промежуточный вывод) — «Материальное положение населения ухудшается»; заключение 2 (окончательный вывод) — «В стране возрастает уровень смертности».

Отметим, что в современных ЭС в базе знаний могут храниться тысячи правил, а коммерческая стоимость одного невыводимого (нового, дополнительного) правила весьма высока.

Главными достоинствами продукционных систем являются простота пополнения и изъятия правил; простота реализации механизма логического вывода и наглядность объяснений результатов работы системы.

Основной недостаток подобных систем — трудность обеспечения непротиворечивости правил при их большом числе, что требует создания специальных правил (так называемых метаправил) разрешения возникающих в ходе логического вывода противоречий. Кроме того, время формирования итогового заключения может быть достаточно большим.

Фреймовая модель. Сравнительно новая модель представления знаний. Само понятие «фрейм» (англ. frame — рама, рамка, скелет, сгусток, сруб и т.д.) было введено в 1975 г. М.Минским (M.Minsky, США).

Фрейм — это минимальная структура информации, необходимая для представления знаний о стереотипных классах объектов, явлений, ситуаций, процессов и др. С помощью фреймов можно моделировать знания о самых разнообразных объектах интересующей исследователя предметной области — важно лишь, чтобы эти объекты составляли класс концептуальных (повторяющихся: стереотипных) объектов, процессов и т. п. Примерами стереотипных жизненных ситуаций могут служить собрание, совещание; сдача экзамена или зачета; защита курсовой работы и др. Примеры стереотипных бытовых ситуаций: отъезд в отпуск, встреча гостей, выбор телевизора, ремонт и др. Примеры стереотипных понятий: алгоритм; действие; методика и др. На рис. 13.2 представлен фрейм технологической операции «соединять» [21].

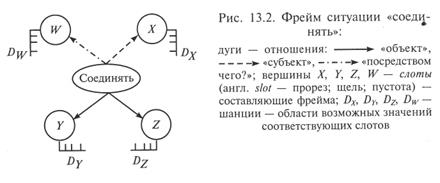
Данный фрейм описывает ситуацию «Субъект X соединяет объект Y с объектом Z способом W».

Наполняя слоты конкретным содержанием, можно получить фрейм конкретной ситуации, например: «Радиомонтажник соединяет микросхему с конденсатором способом пайки». Заполнение слотов шанциями называют активизацией фрейма.

С помощью фреймов можно моделировать как процедурные, так и декларативные знания. На рис. 13.2 представлен пример представления процедурных знаний.

На рис. 13.3 приведен пример фрейма «технологическая операция», иллюстрирующий представление декларативных знаний для решения задачи проектирования технологического процесса.

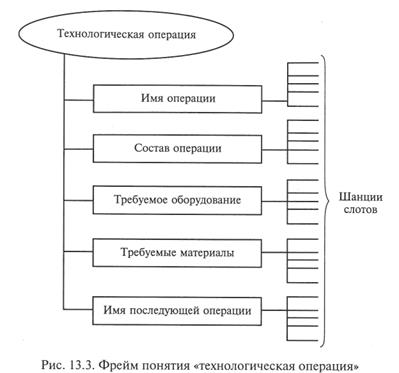
По содержательному смыслу фрейма выделяют [21]:

· фреймы-понятия;

· фреймы-меню;

· фреймы с иерархически вложенной структурой.

Фрейм-понятие — это фрейм типа И. Например, фрейм «операция» содержит объединенные связкой И имена слотов «что делать», «что это дает», «как делать», «кто делает», «где делать» и т.д., а фрейм «предмет» — слоты с именами «назначение», «форма», «вес», «цвет» и т.д.

Фрейм-меню — это фрейм типа ИЛИ. Он служит для организации процедурных знаний с помощью оператора «выбрать». Например, фрейм «что делать» может состоять из объединенных связкой ИЛИ слотов «решить уравнение», «подставить данные», «уточнить задачу» и т.д., причем каждый из этих слотов может иметь несколько значений.

Фрейм с иерархически вложенной структурой предполагает, что в нем в качестве значений слотов можно использовать имена других фреймов, слотов и т.д., т. е. использовать иерархическую структуру, в которой комбинируются другие виды фреймов (в итоге получают так называемые фреймы-сценарии).

Значения слотов могут содержать ссылки на так называемые присоединенные процедуры. Различают два вида присоединенных процедур: процедуры-демоны; процедуры-слуги.

Процедуры-демоны присоединяются к слоту и активизируются при изменении информации в этом слоте (выполняют вспомогательные операции — например, автоматически корректируют информацию во всех других структурах, где используется значение данного слота).

1. Процедура «Если — добавлено» (IF —ADDED) выполняется, когда новая информация помещается в слот.

2. Процедура «Если — удалено» (IF —REMOVED) выполняется, когда информация удаляется из слота.

3. Процедура «Если —нужно» (IF —NEEDED) выполняется, когда запрашивается информация из пустого слота.

Процедуры-слуги активизируются при выполнении некоторых условий относительно содержимого слотов (часто по запросу). Данные процедуры определяются пользователем при создании фрейма. Например, во фрейме «Учебная аудитория» можно предусмотреть слоты «Длина» и «Ширина», а по их значениям вычислять значение слота «площадь».

Фреймы позволяют использовать многие свойства знаний и достаточно широко употребляются. Их достоинства и недостатки схожи с достоинствами и недостатками семантических сетей, которые будут рассмотрены ниже.

Модель семантической сети (модель Куилиана). Семантическая сеть — это направленный граф с поименованными вершинами и дугами, причем узлы обозначают конкретные объекты, а дуги — отношения между ними [21]. Как следует из определения, данная модель представления знаний является более общей по отношению к фреймовой модели (иными словами, фреймовая модель — частный случай семантической сети). Семантическую сеть можно построить для любой предметной области и для самых разнообразных объектов и отношений.

В семантических сетях используют три типа вершин:

· вершины-понятия (обычно это существительные);

· вершины-события (обычно это глаголы);

· вершины-свойства (прилагательные, наречия, определения).

Дуги сети (семантические отношения) делят на четыре класса:

· лингвистические (падежные, глагольные, атрибутивные);

· логические (И, ИЛИ, НЕ);

· теоретико-множественные (множество — подмножество, отношения целого и части, родовидовые отношения);

· квантифицированные (определяемые кванторами общности 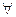и существования ).

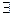(Кванторы — это логические операторы, переводящие одну высказывательную форму в другую и позволяющие указывать объем тех значений предметных переменных, для которых данная выcказывателъная форма истинна).

Приведем два примера.

На рис. 13.4 представлена семантическая сеть для предложения (ситуации) «студент Табуреткин добросовестно изучает новый план счетов на 2002 г. перед сдачей экзамена по дисциплине «Бухгалтерский учет».

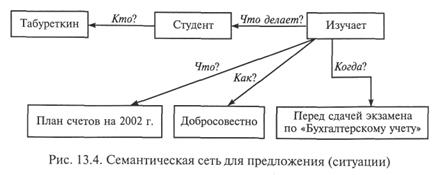
Рис. 13.5 содержит фрагмент семантической сети для понятия «автомобиль».

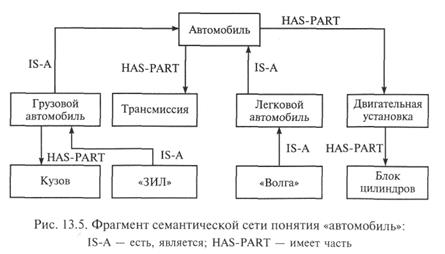
Из приведенных примеров понятно, почему многие специалисты по ИИ считают фрейм частным случаем семантической сети со строго структурированными знаниями.

Основное достоинство методов моделирования знаний с помощью семантических сетей и фреймов — универсальность, удобство представления как декларативных, так и процедуральных знаний. Существует и два недостатка:

· громоздкость, сложность построения и изменения;

· потребность в разнообразных процедурах обработки, связанная с разнообразием типов дуг и вершин.

Модели на основе теоретического подхода.В рамках реализации теоретического подхода применяют логические модели, прежде всего использующие представления знаний в системе логики предикатов. Преимущества такого подхода очевидны: единственность теоретического обоснования и возможность реализации системы путем введения формально точных определений и правил получения выводов. Однако в полной мере претворить в жизнь данный подход даже для «простых» задач оказалось весьма сложно. Поэтому появились попытки перейти от формальной логики к так называемой человеческой логике (модальной логике, многозначной логике и др.), модели которой в большей или меньшей степени учитывают «человеческий фактор», т.е. являются в определенном смысле компромиссными в плане использования и теоретического, и эвристического подходов.

Очень коротко остановимся на ставшей классической предикатной модели представления знаний. Первые попытки использовать такую модель относятся к 50-м гг. прошлого века. Дадим несколько определений.

Пусть имеется некоторое множество объектов, называемое предметной областью. Выражение P(x₁, x₂, ..., х_n), где х₁...x_n — предметные переменные, а Р принимает значения 0 или 1, и называется логической функцией, или предикатом.

Предикат Р(х₁, х₂, ..., х_n) задает отношение между элементами х₁ х₂, ..., х_n и обозначает высказывание, что «х₁, х₂, ..., х_n находятся между собой в отношении Р». Например, если А — множество целых чисел, а Р(а) — высказывание «а — положительное число», то Р(а) = 1 при а > 0 и Р(а) = 0 при а £0.

Из подобного рода элементарных высказываний с помощью логических связок образуют более сложные высказывания, которые могут принимать те же значения — «истина» и «ложь». В качестве связок используются конъюнкция, дизъюнкция, импликация, отрицание, эквивалентность.

Предикат от п переменных называют n-местным.

Одноместные (унарные) предикаты отражают свойства определенного объекта или класса объектов. Многоместные предикаты позволяют записывать отношения, которые существуют между группой элементов.

Если а — тоже предикат, то Р(а) — предикат 2-го порядка и далее до n-го порядка.

Приведем примеры различных предикатов.

1. Унарный предикат (высказывание) «река впадает в Каспийское море» имеет значение 1, если «река» = «Волга», и значение 0, если «Река» = «Днепр».

2. Двухместный предикат «x₁не меньше х₂» может иметь значение 1 или 0 в зависимости от значений х₁и х₂. Если значение предиката тождественно равно 1 при любых значениях предметных переменных, он называется тавтологией.

В аппарат исчисления предикатов входят также символы функций (обычно обозначаемые латинскими буквами f, g, h и т.д.), задаваемых на множестве предметных переменных, и кванторы общности 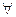и существования .

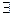3. Представление с помощью предиката знаний, заключенных в теореме Пифагора: P{g[f(x),f(y)],f(z)}, где предикат Р— «быть равным», функция g(x, у) = х + у; функция f(х) = х².

Иногда используется такая форма записи:

РАВНЫ [СУММА (КВАДРАТ(х), КВАДРАТ(y)), КВАДРАТ (z)].

Предикат Р равен 1, если х, у, z — соответственно длины катетов и гипотенузы прямоугольного треугольника.

Как уже отмечалось, предикаты удобны для описания декларативных знаний (фактов, событий и т.п.). Их главные достоинства — возможность реализации строгого вывода знаний (исчисления предикатов) и сравнительная компактность модели. К сожалению, предикаты мало пригодны для записи процедуральных знаний. Кроме того, опыт показал, что человеческое знание по своей структуре много сложнее структуры языков предикатного типа, поэтому требуются специальные навыки «подгонки» структуры реального знания под структуру модели (как правило, значительно обедняющей исходные знания).