Модульное программирование

Обычно, в реальной программе имеются некоторые участки, к которым происходит обращение из разных ее мест. Такие фрагменты программы удобно вынести в отдельные подпрограммы (модули), что значительно улучшает обозримость программы и сокращает ее размер. В Бейсике имеется два вида процедур – процедура-функция и просто процедура.

¶ПРОЦЕДУРА-ФУНКЦИЯорганизуется следующей конструкцией

üFUNCTION имя_функции [(список_параметров)]

Операторы

имя функции=выражение

Операторы

END FUNCTION

Здесь:

имя функции – произвольно задаваемое по правилам языка имя.

список параметров – перечень переменных, которые передаются в функцию для обработки.

имя функции=выражение – этим оператором функции присваивается результат, который и передается в вызывающую часть программы.

Результатом процедуры-функции является только одно значение. К процедуре-функции можно обратиться в точности так же, как и к обычной функции, включив его в текст любого оператора.

Для осуществления возможности обращения к процедуре-функции в старшей по отношению к ней программе (программе, из которой происходит вызов функции) должен присутствовать оператор объявления функции

üDECLARE FUNCTION имя_функции ([аргументы])

Здесь аргументы – список переменных и констант, которые передаются из главной программы в функцию. По типу и числу список аргументов должен совпадать со списком параметров в самой функции, однако сами имена могут быть разными.

Пример. Организуем функцию вычисления факториала fakt(). Факториалом числа Х! называется произведение всех целых чисел от 1 до самого числа Х, например, 4!=1*2*3*4.

DECLARE FUNCTION fakt (y)'главная программа

PRINT fakt(3)

END

FUNCTION fakt (m)'функция вычисления факториала

k = 1

FOR i = 1 TO m: k=k*i: NEXT

fakt = k'присвоение значения функции

END FUNCTION

Здесь в функцию передается аргумент – число 3, которое в функции получает имя M. Результат вычислений факториала формируется оператором fakt = k, который и печатается в главной программе (PRINT fakt(3)).

¶ПРОЦЕДУРАявляется более мощным средством и организуется структурой

üSUB имя_процедуры [(список_параметров)]

Операторы

END SUB

Здесь перечисленные параметры имеют тот же смысл, что и в процедуре-функции, однако, в отличие от последней, она может возвращать несколько значений в вызывающую программу через список параметров. Вызов процедуры осуществляется специальным оператором

üCALL имя_процедуры [(список_параметров)]

Передаваемые параметры являются как аргументами процедуры, так и, возможно, ее результатами.

В программе, из которой происходит вызов функции, следует объявить процедуру оператором

üDECLARE SUB имя_процедуры [(аргументы)]

Пример. Пусть по известным высоте (h=4) и ширине (l=5) прямоугольника нужно найти и напечатать его периметр (perimetr) и площадь (plosh). В операторе вызова этим аргументам соответствуют значения – 4, 5, x, y, а в процедуре – a, b, c, d.

DECLARE SUB pr(h, l, perimetr, plosh)'главная программа

CALL pr(4, 5, x, y)'вызов процедуры

PRINT “Периметр=”;x,“Площадь=”;y'печать результатов

END

SUB pr (a,b,c,d)'процедура вычисления элементов прямоугольника

c=2*(a+b)

d=a*b

END SUB

Для процедур-функций и процедур имеются свои операторы выхода:

üEXIT FUNCTION

üEXIT SUB

Оператор EXIT SUB возвращает управление на оператор, следующий после оператора CALL.

2.7. обРАБОТКА Символьных данных

Все символы в ПК имеют уникальные коды, значения которых закреплены в ASCII-таблице. С ней можно ознакомиться в любом справочнике.

В Бейсике имеются несколько функций и операторов обработки символьных данных.

üLTRIM$(символьное_выражение) –удаляет начальные про­белы в символьном выражении.

üRTRIM$(символьное_выражение) –удаляет конечные пробелы в символьном выражении.

üSPACE$(числовое_выражение) –возвращает строку пробелов длиной N символов (N в пределах 0-32767).

üSTRING$(длина_строки, код_символа или символ) –возвращает строку длиной длина строки из символов, заданных непосредственно или своим кодом.

Пример. ?STRING$(6,”+”) Результат: “+++++”

üINSTR([начальная_позиция],строка1, строка2) –возвращает позицию первого вхождения строки2 в строку1, начиная с начальной позиции. Если начальная позиция не задана, отсчет производится с начала.

Пример. ?INSTR(”Саша”,”а”),INSTR(3,”Саша”,”а”) Результат: 2,4

üLEFT$(символьное_выражение, n) –возвращает строку, содержащую n первых символов.

Пример. ?LEFT$(”Саша”,2) Результат: ”Са”

üRIGHT$(символьное_выражение, n) –возвращает строку, содержащую n последних правых символов.

Пример. ?RIGHT$(”Саша”,2) Результат: ”ша”

üMID$(символьное_выражение, начальная_позиция [,длина]) –возвра­щает фрагмент символьного выражения, с начальной позиции заданной длины.

Пример. ?MID$(”теория”,4), MID$(”теория”,4,2) Результат:”рия”, ”ри”

üMID$(строка, начальная_позиция [,длина])=символьное_выражение –символьный оператор, заменяющий фрагмент строки на сим­вольное выражение, начиная с начальной позиции заданной длины.

Пример. x$ = "здесь вход"

MID$(x$, 7, 2) = "выход"

PRINT x$ Результат: "здесь выхо"

üSTR$(числовое_выражение) –возвращает символьное представление числа или числового выражения.

Пример. STR$(3) Результат: "3"

üVAL(символьное_выражение) –возвращает числовое представление символьного выражения. Функция обратна функции STR$().

Пример. STR$("3") Результат: 3

üLEN(символьное_выражение) –возвращает длину символь­ного выражения.

Пример. LEN(”теория”) Результат: 6

üASC(символ) –возвращает код символа ПК.

üCHR$(число) –возвращает символ по его коду.

Примеры. ASC(“R”) Результат: 82 (код буквы R=82)

CHR(82) Результат: “R”

Т.е. функции эти обратны друг другу.

Текстовые данные можно сравнивать между собой на больше, меньше, равно. Сравниваются, конечно, не сами символы, а их коды. Так верным будет отношение “A”<”R”, поскольку ASCII-код (65) английской буквы А меньше кода (85) буквы R. Сравнивать можно и целые слова. Так верно отношение “TOM”>”JON”. Сравнение начинается с первой пары символов. Здесь код английской T (код 84) больше кода J (74). Остальные символы далее не сравниваются. Если же первая пара букв совпадает, будет проверена следующая пара и т.д. до первого несовпадения. Если число символов в сравниваемых словах различно, сравнение выполняется до исчерпания первого операнда. Рост кодов символов соответствуют их порядку в алфавите. Для русских символов это не совсем так (см. справочник).

Пример. Напечатать символьную переменную X$ в обратном порядке

x$="Внимание": y$ =""

FOR i = LEN(x$) TO 1 STEP -1

y$ = y$ + MID$(x$, i,1)

NEXT

PRINT y$Результат: “еинаминВ“

Здесь в переменной y$ формируется нужный результат.

& Тест. 2.7.1. Чему будет равно Х после завершения программы? 1). 456128, 2).561234, 3).341285.

y$=”123456”

x$= RIGHT$(y$,3)+LTRIM$(STR$(VAL(LEFT$(y$,3))+5))

ЧИСЛЕННЫЕ МЕТОДЫ АНАЛИЗА

Важнейшая область приложения программирования – инженерные расчеты. Здесь широко используются методы вычислительной математики. Рассмотрим некоторые из популярных численных методов.

¶Вычисление определенного интеграла.Аналитическое интегрирова­ние возможно лишь для небольшого класса “табличных” функций. В других случаях приходится прибегать к приближенным методам. Нахождение определенного интеграла заключается в вычислении площади под подинтегральной функцией в заданном диапазоне аргумента. Самый простой, но и самый грубый метод – метод прямоугольников (рис. 2.8.1).

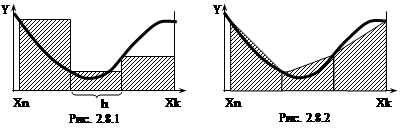Здесь диапазон интегрирования от начальной точки Xn до конечной Xk разбивается на небольшие участки (всего N участков) с основанием h. Сумма площадей всех участков (Y(Xi)*h) и будет считаться интегралом.

Xk n–1

S =òY(x)dX » åY(Xi)*h

Xn i=1

Приближенным значением интеграла S считаем сумму площадей всех прямоугольников под кривой (на рисунке заштрихованы). Видим, что погрешность метода весьма велика. Более точным является метод трапеций (рис. 2.8.2). Площадь элементарной трапеции (h[Y(Xi)+Y(Xi+h)]/2) гораздо лучше приближа­ется к кривой.

Программа (для функции Y=X2), реализующая оба метода, приведена ниже.

h=0.1: s=0'задание шага h

Xn = 0: Xk = 5'задание пределов интегрирования

FOR x = Xn TO Xk- h STEP h'изменение текущих точек

's=s+h*x^2'метод прямоугольников

s=s+h*(x^2+(x+h)^2)/2'метод трапеций

NEXT

PRINT s

Отличие методов заключается лишь в одном операторе. Для метода прямоугольников он показан как комментарий.

Следует отметить, что при уменьшении шага интегрирования погрешность любого метода снижается, но поскольку метод трапеций более точен, здесь необходимая точность будет достигнута быстрее.

¶Определение действительных корней нелинейных алгебраических уравнений.Часто исследование математических моделей, например технологических процессов, приводит к необходимости решить то или иное алгебраическое уравнение, причем во многих случаях прямое аналитическое решение его затруднено или невозможно. Например, невозможно аналитически решить любое уравнение пятой степени. В связи с вышесказанным, были разработаны приближенные численные методы определения корней таких уравнений. Численное решение нелинейных алгебраических уравнений проводят в два этапа.

На ПЕРВОМ этапе необходимо отделить корни, т.е. найти такие интервалы изменения переменной, где расположен один корень.

Пусть задано уравнение: F(X,P1,P2, ... ,Pn) = 0.

Здесь: F – заданная функция,

X – неизвестная величина,

P1, P2, ..., Pn – коэффициенты.

Решить заданное уравнение – значит найти значения X (корни) ему удовлетворяющие. При любых других значениях F(X,P1,P2, ... ,Pn)#0.

Если заменить уравнение функцией Y=F(X,P1,P2,...Pn), а затем нарисовать ее график, то точки пересечения функцией оси Х и будут ее корнями. Признаком наличия корня на интересующем отрезке может служить противоположность знаков функции на его концах. Формальным признаком, удобным для программирования, является отрицательность произведения значений функции на концах отрезка.

На ВТОРОМ этапе определяют точное значение каждого корня.

Одним из самых простых методов такого определения является метод половинного деления. Суть метода иллюстрирует рис. 2.8.3 для функции Y=F(x). Положим, что определены границы интервала [a,b], внутри которого находится один корень функции Y=F(x). Исходный диапазон АВ делится пополам. Определяется тот из двух новых отрезков, на котором находится корень. На рисунке это отрезок АВ1. Этот новый отрезок снова делим пополам, снова определяем участок, на котором находится корень (А1В1). Затем снова (А2В1) и т.д. до тех пор, пока очередной отрезок не станет <E. Тогда в качестве корня можем взять любую из, ограничивающих последний отрезок, точек, например А. Формальным признаком пересечения кривой оси Х и наличия на участке корня являются разные знаки функции на краях отрезка. Иными словами – отрицательность произведения значений Y в этих точках. Алгоритм решения изображен на рис. 2.8.4, а программа ниже.