Примеры решения типовых задач. Задача 1. Вычислить значение функции y=b-sin2x*cos(ax)
Задача 1. Вычислить значение функции y=b-sin2x*cos(ax). Значения а, bи х вводить с клавиатуры.
Таблица 7
Таблица обозначений в программе
| Наименование | Обозначение | Тип данных |
| Функция | У | real |
| Аргумент | X | real |
| Коэффициенты | а, b | real |
Программа:
Program Prim5;
var х,у,a, b:real;
Begin
writeln('Введите значения a,b,x');
readln (a,b,х) ; {вводим исходные данные с клавиатуры}
у : =b-sin (2*х) *cos (а*х) ; {вычисляем у}
writeln (у) ; {выводим на экран вычисленное значение }
End.
Задача 2. Составить программу расчета значений функции f(x)=sin(2x) *е * на интервале изменениях, равном[а,b] вn равноотстоящих точках. Вычисленные значения функции сохранить в массивес.Определить: 1) сумму вычисленных значений функции, 2) произведение отрицательных значений функции из числа вычисленных, 3) количество значений функции среди вычисленных, целая часть которых делится на 2 без остатка, 4) наибольшее из вычисленных значений функции. Значенияa, b, n вводить с клавиатуры (а<b иn>1).
Таблица 8
Таблица обозначений в программе
| Наименование | Обозначение | Тип |
| Аргумент функции | X | real |
| Границы интервала изменения х | а, b | real |
| Кол-во точек | n | integer |
| Шаг изменения аргумента х | d | real |
| Сумма значений функции | s | real |
| Произведение отрицательных значений функции | Р | real |
| Количество значений функции, целая часть которых делится на 2 без остатка | kol | integer |
| Наибольшее из вычисленных значений функции | max | real |
| Массив, содержащий вычисленные значения функции | с | real |
| Текший номер расчетной точки | і | integer |
Комментарий к программе. Для вычисления значений функции организуем цикл, в котором при изменяющемся значении аргумента функции х будем вычислять значения функции и записывать эти значения в массивс.Аргументх изменяется ота доb с шагомd, который равен длине интервала изменениях, деленной на количество расчетных точек минус 1, т.е. d: = (b-a)/ (n-1).
Таким образом, значение элемента массива с [1] равно значению функции в точкеа (точка с номером1), значение элементас [2] равно значению функции в точкеa+d (точка с номером 2) и т.д. Сумма вычисленных значений функции сеть сумма значений всех элементов массивас. Произведение отрицательных значений функции из числа вычисленных есть произведение элементов массивас, имеющих отрицательные значения. Количество значений функции среди вычисленных, целая часть которых делится на 2 без остатка есть количество элементов массивас, удовлетворяющих этому условию. Наибольшее из вычисленных значений функции есть наибольший по значению элемент в массивес.
Программа:
program Ргіm6;
Var
x,a,b,s,d,p,max:real;
і,n,kol:integer;
c:array [1..100] of real;
Begin
writeln ('Введите a,b (a<b)');
readln (a,b); writeln('Введите l<n<=100');
readln (n); d: = (b-a)/ (n-1) ; {вычисляем шаг изменения x}
{Вычисляем значения функции и сохраняем их в массиве}
х:=а; і:=1;
while i<=n do
Begin
с [і] : =sin (2*x) *exp (x); {вычисляем значение f(x) }
writeln (x, c[i]); {вывод на экран значения х и f (х) }
і : =і + 1; х : =x+d; {переходим к следующей расчетной точке }
End;
{Определяем сумму, произведение, количество и наибольшее значение}
s:=0; р:=1; kol:=0; тах:=с[1];
for i:=l to n do
Begin
s : =s+c [i] ; {накапливаем сумму в цикле}
if c[i]<0 then p :=p*c [і ];{накапливаем произведение}
if trunc(c[i]) mod 2 =0 then kol:=kol +l; {накапл. кол-во}
if c[i]>max then max:=c[i] ; {определяем наиб, зн-е}
End;
{Выводим результаты расчета на экран}
writeln(‘ сумма =',s);
writeln(‘произведение = ',р);
writeln(‘количество значений функции =' ,kol) ;
writeln(‘наибольшее значение функции =' ,тах) ;
End.
Задача 3. Найти минимальный по значению элемент в двумерном массивеа, состоящем изn строк иm столбцов, значенияn,m вводятся с клавиатуры.
Таблица 9
Таблица обозначений в программе
| Наименование | Обозначение | Тип |
| Массив | а | real |
| Кол-во строк и столбцов в массиве | n, m | integer |
| Минимальное значение | min | real |
| Индекс | і/ j | integer |
Программа:
Program Prim7;
Var
a:array[l..10,1..10] of real;
i,j,n,m: integer;
min: real;
Begin
writeln('вводим размеры массива') ;
write('число строк n='); readln(n);
write('число столбцов m=');
Readln(m);
{вводим значения элементов массива с клавиатуры}
for i:=l to n do
for j:=1 to m do
readln(a[i,j ]);
{находим наименьший по значению элемент массива}
min:=а[1,1];
for i:=l to n do
for j:=1 to m do
if a[i,j]< min then min:=a[i,j];
writeln('минимальное значение=',min);
End.
Тестовые задания:
1. Для типа данных REAL в языке программирования Pascal не определена операция …
| 1. ^ (возведение в степень) | |||
| 2. / (деление) | |||
| 3. * (умножение) | |||
| 4. + (сложение) |
2. Принципиальным отличием языков программирования от естественных человеческих языков является …
| 1. однозначность | |||
| 2. ограниченность | |||
| 3. универсальность | |||
| 4. простота |
3.Стандартной процедурой языка программирования, преобразующей данные из внутреннего представления в символы, выводимые на экран, является …
| 1. вывод | |||
| 2. ввод | |||
| 3. присваивание | |||
| 4. печать |
4.Форма внутреннего представления данных является свойством следующего понятия языков программирования …
| 1. тип данных | |||
| 2. подпрограмма | |||
| 3. оператор | |||
| 4. модуль |
5.Структурированный тип данных из однородного упорядоченного набора величин одного и того же типа, объединенных одним общим именем, называется …
| 1. массивом | |||
| 2. записью | |||
| 3. файлом | |||
| 4. множеством |
6.Языки программирования, для которых имеются компиляторы, работающие более чем на одной аппаратной платформе или операционной системе, называются …
| 1. кроссплатформенными | |||
| 2. универсальными | |||
| 3. многоуровневыми | |||
| 4. гетерогенными |
7.Операцией отношения языка программирования Pascal, является …
| 1. < > (не равно) | |||
| 2. and (логическое и) | |||
| 3. / (деления) | |||
| 4. + (сложения) |
8.При описании сложных объектов, которые характеризуются различными свойствами, а также при создании различных информационных систем используются …
| 1. записи | |||
| 2. массивы | |||
| 3. интервалы | |||
| 4. множества |
9.Среди представленных имен переменных неправильным является …
| 1. 100%_praviljnoe_imya | |||
| 2. Nepraviljnoe_imya | |||
| 3. Nevernyj_identificator | |||
| 4. Identifikator_100%_vernyj |
10.В программе на языке программирования Pascal раздел операторов начинается со служебного слова …
| 1. BEGIN | |||
| 2. REPEAT | |||
| 3. OPERATOR | |||
| 4. PROCEDURE |
11.В языке программирования Pascal оператор GOTO является оператором …
| 1. безусловного перехода | |||
| 2. условного перехода | |||
| 3. ветвления | |||
| 4. выбора |
12.Языки программирования высокого уровня по отношению к аппаратным средствам компьютера являются …
| 1. машинно-независимыми | |||
| 2. машинно-зависимыми | |||
| 3. аппаратно-ориентированными | |||
| 4. процессорно-совместимыми |
Лабораторная работа №5
Тема: СИСТЕМЫ СЧИСЛЕНИЯ
Цель работы:Получение практических навыков перевода чисел из одной системы счисления в другую, проведение арифметических операций над числами в различных системах счисления.
Задание:Выполнить примеры по переводу чисел из одной системы счисления в другую и арифметическим действиям над числами в различных системах счисления.
Литература: [1]-стр. 67-80, [2]-стр. 45-51.
Все фантастические возможности вычислительной техники (ВТ) реализуются путем создания разнообразных комбинаций сигналов высокого и низкого уровней, которые условились называть «единицами» и «нулями».
Под системой счисления (СС) понимается способ представления любого числа с помощью алфавита символов, называемых цифрами.
СС называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.
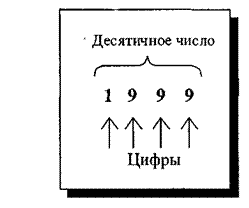 Десятичная СС является позиционной. На рисунке слева значение цифры 9 изменяется в зависимости от, ее положения в числе. Первая слева девятка делает вклад в общее значение десятичного числа 900 единиц, вторая — 90, а третья — 9 единиц.
Десятичная СС является позиционной. На рисунке слева значение цифры 9 изменяется в зависимости от, ее положения в числе. Первая слева девятка делает вклад в общее значение десятичного числа 900 единиц, вторая — 90, а третья — 9 единиц.
Римская СС является непозиционной.Значение цифры X в числе XXI остается неизменным при вариации ее положения в числе. Количество различных цифр, употребляемых в позиционной СС, называется основаниемСС. В десятичной СС используется десять цифр: 0,1,2,..., 9; в двоичной СС — две: 0 и 1; в восьмеричной СС — восемь: 0, 1,2, ..., 7. В СС с основанием Q используются цифры от 0 до Q - 1.
В общем случае в позиционной СС с основанием Q любое число х может быть представлено в виде полинома:
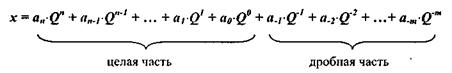
где в качестве коэффициентов, могут стоять любые цифры, используемые в данной СС.
Принято представлять числа в виде последовательности входящих в полином соответствующих цифр (коэффициентов):
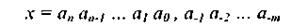
Запятая отделяет целую часть числа от дробной части. В ВТ чаще всего для отделения целой части числа от дробной части используют точку. Позиции цифр, отсчитываемые от точки, называют разрядами. В позиционной СС вес каждого разряда отличается от веса (вклада) соседнего разряда в число раз, равное основанию СС. В десятичной СС цифры 1-го разряда — единицы, 2-го — десятки, 3-го — сотни и т. д.
В ВТ применяют позиционные СС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную системы и др. Для обозначения используемой СС числа заключают в скобки и индексом указывают основание СС: (15)10;(1011)2;(735)8;(1EA9F)16. Иногда скобки опускают и оставляют только индекс: 1510; 10112;7358; 1EA9FI6.
Есть еще один способ обозначения СС: при помощи латинских букв, добавляемых после числа. Например, 15D; 1011B;735Q; 1EA9FН.
Установлено, что, чем больше основание СС, тем компактнее запись числа. Так двоичное изображение числа требует примерно в 3,3 раза большего количества цифр, чем его десятичное представление. Рассмотрим два числа: 97D = 1100001В. Двоичное представление числа имеет заметно большее количество цифр.
Несмотря на то, что десятичная СС имеет широкое распространение, цифровые ЭВМ строятся на двоичных (цифровых) элементах, так как реализовать элементы с десятью четко различимыми состояниями сложно
Указанные устройства не нашли применения для построения средств ВТ. Историческое развитие вычислительной техники сложилось таким образом, что цифровые ЭВМ строятся на базе двоичных цифровых устройств (триггеров, регистров, счетчиков, логических элементов и т. п.).
Шестнадцатеричная и восьмеричная СС используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов— команд, данных, адресов и операндов. Перевод из двоичной СС в шестнадцатеричную и восьмеричную СС (и обратно) осуществляется достаточно просто.
Без знания двоичной СС невозможно понять принципы архивации, криптографии и стеганографии. Без знания двоичной СС и булевой алгебры невозможно представить, как происходит слияние объектов в векторных графических редакторах. В табл. 1 приведены некоторые числа, представленные в различных СС.
Рассмотрим правило перевода из восьмеричной СС в двоичную СС. Для перевода восьмеричного числа в двоичную СС достаточно заменить каждую цифру восьмеричного числа соответствующим трехразрядным двоичным числом. Затем необходимо удалить крайние нули слева, а при наличии дробной части — и крайние нули справа.
Еще одно правило перевода чисел. Для перевода от шестнадцатеричной СС к двоичной ССкаждая цифра шестнадцатеричного числа заменяется соответствующим четырехразрядным двоичным числом. У двоичного числа удаляются лидирующие нули (крайние слева), а если имеется дробная часть, то и крайние правые нули.
Пример 1. Перевести число 305.4Q из восьмеричной СС в двоичную СС.
Решение.
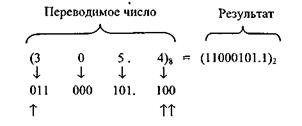
Отмеченные символами «á» нули следует отбросить. Заметим, что двоичные числа взяты из табл. 1.
Таблица 1- Числа от 0 до 15, представленные в различных системах счисления
| Системы счисления | |||
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| А | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Рассмотрим еще одно правило. Для перехода от двоичной СС к восьмеричной(или шестнадцатеричной)СС поступают следующим образом: двигаясь от точки сначала влево, а затем вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости пулями крайние левую и правую группы. Затем каждую группу из трех (четырех) разрядов заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Для перевода двоичногочисла в десятичнуюСС достаточно представить число в виде полинома, подставить в него известные коэффициенты и вычислить сумму.
Перевод целых чисел из десятичной СС в двоичную, восьмеричную или шестнадцатеричную СС удобно делать с помощью следующего правила:
Для перевода целого числа из S-системы счисления в W-систему счисления нужно последовательно делить это число, а затем получаемые частные на основание W новой СС до тех пор, пока частное не станет меньше W.
При переводе наиболее частой ошибкой является неверная запись ре- зультата. Запись двоичного числа следует начинать со старшего значащего разряда (СЗР), а заканчивать записью младшего значащего разряда (МЗР). Следует помнить, что при делении первым получается значение МЗР.
Для перевода правильной дроби из S-системы счисления в СС с основанием W нужно умножить исходную дробь и дробные части получающихся произведений на основание W, представленное в старой S-системе. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в W- системе счисления.
Напомним, что правильнойназывается дробь, числитель которой меньше знаменателя.
Обычно перевод дробей из одной СС в другую производят приближенно. При переводе неправильной дроби переводят отдельно целую и дробную части, руководствуясь соответствующими правилами.
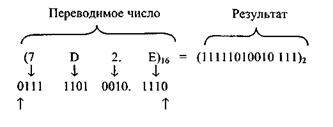
Пример 2. Перевести число 7D2.EH из шестнадцатеричной СС в дво- ичную СС. Решение.
Пример3. Перевести число 111001100.001В из двоичной СС в восьмеричную СС. Решение

Пример 4.Перевести число 10111110001.0012 из двоичной СС в шестнадцатеричную СС.
Решение Для перевода двоичногочисла в десятичнуюСС достаточно представить число в виде полинома, подставить в него известные коэффициенты и вычислить сумму.
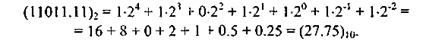
Пример 5. Перевести шестнадцатеричное число 2Е5.А16 в десятичную СС. Решение. 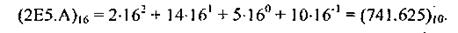
Перевод целых чисел из десятичной СС в двоичную, восьмеричную или шестнадцатеричную СС удобно делать с помощью следующего правила:
Для перевода целого числа из S-системы счисления в W-систему счисления нужно последовательно делить это число, а затем получаемые частные на основание W новой СС до тех пор, пока частное не станет меньше W.
Пример 6. Перевести целое десятичное число 3710 в двоичную СС: Решение
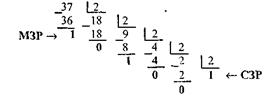
Результат перевода: (37)10 = (100101)2.
При переводе наиболее частой ошибкой является неверная запись ре- зультата. Запись двоичного числа следует начинать со старшего значащего разряда (СЗР), а заканчивать записью младшего значащего разряда (МЗР). Следует помнить, что при делении первым получается значение МЗР.
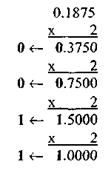 Для перевода правильной дроби из S-системы счисления в СС с основанием W нужно умножить исходную дробь и дробные части получающихся произведений на основание W, представленное в старой S-системе. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в W- системе счисления.
Для перевода правильной дроби из S-системы счисления в СС с основанием W нужно умножить исходную дробь и дробные части получающихся произведений на основание W, представленное в старой S-системе. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в W- системе счисления.
Напомним, что правильнойназывается дробь, числитель которой меньше знаменателя.
Пример7. Перевести правильную десятичную дробь 0.187510 в двоичную СС. Решение.
Запишем результат перевода: 0.187510 = 0.00112. Обычно перевод дробей из одной СС в другую производят приближенно. При переводе неправильной дроби переводят отдельно целую и дробную части, руководствуясь соответствующими правилами.
Пример 8.Перевести десятичное число 9.62510 в двоичную СС.
Решение: Вначале переведем целую часть десятичного числа в двоичную СС: 910= 10012. Затем переведем правильную дробь: 0.62510 = 0.1012. Окончательный ответ: 9.62510= 1001.1012.
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения (табл. 2), над восьмеричными и шестнадцатеричными числами (Приложения А и Б).
Таблица 2- Арифметические действия над двоичными числами
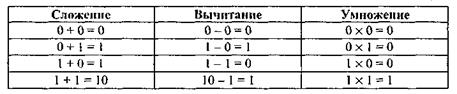
Правила арифметики во всех позиционных СС аналогичны. В двоичной СС арифметическое сложение происходит по правилу сложения по модулю два с учетом переноса единицы в старший разряд (см. табл. 2).
В устройствах, реализующих операцию арифметического сложения двоичных чисел, операнды представляют числами определенной разрядности (одинаковой для обоих операндов). При этом неиспользуемые старшие разряды заполняются нулями. Также заполняются пулями младшие разряды дробной части вещественного числа (справа от точки).
Следует заметить, что в реальных ЭВМ чаще всего используются 32-, 64-, 128-разрядные сетки (машинные слова). Однако, для учебных целей при рассмотрении правил выполнения арифметических операций не будем обращать внимание па разрядность операндов (будем использовать разрядность отличающуюся от разрядности реальных ЭВМ).
При сложении вещественных чисел в общем случае перенос осуществляется и из дробной части числа в целую часть.
Рассмотрим правило умножения многоразрядных двоичных чисел.
Умножение двоичных многоразрядных чисел производится путем образования частичных произведений и последующего их суммирования Каждое частичное произведение равно пулю, если в соответствующем разряде множителя стоит 0, или равно множимому, сдвинутому на соответствующее число разрядов влево, если в разряде множителя стоит 1.
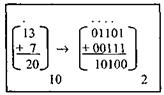
Пример 1.Выполнить операцию арифметического сложения в двоичной системе счисления. Решение: Точками показаны переносы.
Пример2. Выполнить операцию арифметического сложения двух вещественных чисел в двоичной системе счисления. Решение:
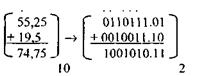
При сложении вещественных чисел в общем случае перенос осуществляется и из дробной части числа в целую часть.
Рассмотрим правило умножения многоразрядных двоичных чисел.
Умножение двоичных многоразрядных чисел производится путем образования частичных произведений и последующего их суммирования Каждое частичное произведение равно пулю, если в соответствующем разряде множителя стоит 0, или равно множимому, сдвинутому на соответствующее число разрядов влево, если в разряде множителя стоит 1.
Таким образом, операция умножениямногоразрядных двоичных чисел внутри ЭВМ сводится к операции сдвига и сложения.Положение точки, отделяющей целую часть от дробной части, определяется так же, как и при умножении десятичных чисел.
Пример 3. Перемножить в двоичной СС числа 7.510 и 510. Решение:
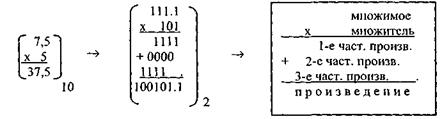
В рассмотренном примере второй разряд множителя равен нулю, по этому второе частичное произведение также равно нулю.
Индивидуальные задания
1. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления (до шестого знака после запятой).
2. Переведите числа в десятичную систему счисления.
3. Переведите числа в двоичную систему счисления.
4. Выполните сложение чисел.
5. Выполните вычитание чисел.
6. Выполните умножение чисел.
В заданиях 4-6 проверять правильность вычислений переводом исходных данных и результатов в десятичную систему. Для каждого задания привести подробный расчет.
Вариант 1.
1. 25510, 139810, 464,9410
2. 11000010012, 356 8, АF8,2116.
3. 4628 , 2В616.
4. 10111101102 + 10010110012, 11100010002+ 10111102, 5478+1358, 2В616 +21А716.
5. 11000010012 – 1101101102, 1110000112-100111112, 10678 – 7778, АF8,2116 -35416 .
6. 1678 * 778, А716 * 18816, 11100010002 * 10111102.
Вариант 2.
1. 1387610, 146,2510, 712,9410 .
2. 1111111102, 7778, 35416 .
3. 10678, 16В16.
4. 10110101112 + 10111101012, 11100010002 + 10111102, 34678 + 6478, 6В16 + 3А616.
5. 11100010002 – 10111102, 11100110002-101001012 455618 - 166218, 16В16 - 2В616.
6. 16В16 * 2В616, 10678*462 8, 1111111102* 1011112.
Вариант 3.
1. 5670910, 2428,510, 340,6610 .
2. 100000101002, 106178, 13А16 .
3. 657238, 175F0316.
4. 11000110002+100000101002, 100111001112+100011111112, 6528+ 3678, 239А16 + 9С416.
5. 10011000112 – 1111111102, 1110000002-100111112, 6578-3678, 239А16 – 9С416.
6. 6578 *3678, 18416 * 35416, 1110002*1110112.
Вариант 4.
1. 2378,2510, 678510, 6788,4610 .
2. 111111101102, 356778, 95АВ16.
3. 2774038, 95АВ 16 .
4. 111111101012+110011100012, 1000111112 + 10011111012, 239А16 + 9С416, 74038+2778.
5. 239А16 – 9С416, 10111101102 - 10010110012, 1110000102-100101112, 74038-2778.
6. 11011012 * 1101102, 74038*2778, 239А16 * 9С416.
Вариант 5.
1. 464410, 3448,9710, 387,2510 .
2. 111000111002, 46748, АF8,2116.
3. 4628, 479АF16 .
4. 10111101102+10010110012, 1001101102+100101010112, 547АF16 +45FC16, 7318+1728.
5. 11000010012 – 1101101102, 1110011002-10011110012, 479АF16 -45FC16, 7318-1728.
6. 2378 * 1678, 111110012 *11101102, EFD16*12F16.
Вариант 6.
1. 720,9410, 788,510, 226910.
2. 11101001011002, 7778 САF8,2116.
3. 10678, АВ8,2116 .
4. 10110101112 + 10111101012, 100111001112+100011111112, 6578+ 3678, 239А16 + 9С416.
5. 11100010002 – 10111102, 1110000112-100111002, 6578-3678, 239А16-9С416.
6. 16В16 * 2В616, 6578* 3678, 10001112 * 100001112.
Вариант 7.
1. 290,4610, 190610 , 24610.
2. 11100011111002, 46548, 13В,А216 .
3. 15678, 17F0316.
4. 11000110002 +100000101002, 100111001112+100011111112, 1378+ 3478, 4569А16 + 9F416.
5. 10011000112 – 1111111102, 1110001102-100110112, 1378-3478, 4569А16 - 9F416.
6. 18416 * 35416, 111002*111112, 1378*3478.
Вариант 8.
1. 756,2510, 590,2510 , 278610.
2. 111111101102, 23748, АСВ8,2116.
3. 2774038, 14С216.
4. 111111101012+1100111100012, 100111001112+100011111112, 6538+ 5678, 239А16 + 9С416.
5. 1110000002-100111112, 100111001112-100011111112, 6538-5678, 239А16 – 9С416.
6. 11011012 * 1101102, 6538*5678, 239А16 * 9С416.
Тестовые задания: Тема «Системы счисления»
1. Для кодирования 20 различных состояний достаточно ________ двоичных разрядов
1. 8
2. 20
3. 5
4. 32
2. Если числа в двоичной системе счисления имеют вид 110012 и 10102, то их сумма в двоичной системе счисления равна …
1. 1011112
2. 1010102
3. 111002
4. 1000112
3. Результат вычисления выражения 16*8 + 4*4 + 1 имеет в двоичной системе счисления вид …
1. 112001
2. 10010001
3. 122001
4. 10011001
4. Если числа в двоичной системе счисления имеют вид 112 и 1012, то их произведение в десятичной системе счисления равно …
1. 15
2. 60
3. 1111
4. 8
5. Число 102310 в двоичной системе счисления имеет вид
1. 0011000000
2. 1000001111
3. 1111111111
4. 1000000001
6. Укажите упорядоченную по возрастанию последовательность значений
1. 558 557 5516
2. 558 5516 557
3. 5516 558 557
4. 557 558 5516
7. Если числа в пятеричной системе счисления имеют вид 1215 и 445, то их разность в десятичной системе счисления равна …
1. 10
2. 21
3. 12
4. 77
8. Если числа имеют вид 318 и А16, то их разность в двоичной системе счисления равна …
1. 11112
2. 111112
3. 101012
4. 11102
9. Задано число 100101112 . В четверичной системе счисления это число имеет вид
1. 507
2. 213
3. 2112
4. 2113
10. Определите, в какой системе счисления записано математическое выражение 123 + 2 = 131
1. В троичной
2. В пятеричной
3. В восьмеричной
4. В четверичной
Лабораторная работа № 4
Тема: ТЕХНОЛОГИИ ОБРАБОТКИ ТЕКСТОВЫХ ДОКУМЕНТОВ В MS WORD
Цель работы:Получение практических навыков использования текстового процессора MS Word при подготовке, редактировании и оформлении текстовой документации, графиков, диаграмм, рисунков.
Задание: По указанной литературе, методическим указаниям к данной работе и Приложению изучить порядок работы с программой (приложением) MS Word. Ответить на контрольные вопросы.
Литература: [1]-стр. 202-278, [2]-стр. 198-251.
Перечень заданий по Word
1. Работа со шрифтами.
2. Форматирование абзацев.
3. Форматирование страниц.
4. Поиск, замена.
5. Колонтитулы, нумерация страниц.
6. Проверка орфографии, синонимы.
7. Специальные символы; кадры, буквицы.
8. Колонки текста (газетный формат).
9. Создание и оформление таблиц.
10. Нумерованные, маркированные, многоуровневые списки.
11. Встраивание графических объектов.
12. Создание схем и простейших рисунков.
13. Оформление титульных листов (объект Word Art).
14. Редактор формул.
15. Создание и оформление оглавлений, установка параметров листа.
16. Создание гиперссылок.
