Алгоритмическое определение булевских операций

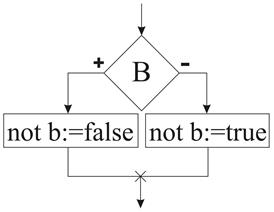
Отрицание

Конъюнкция

a) b)

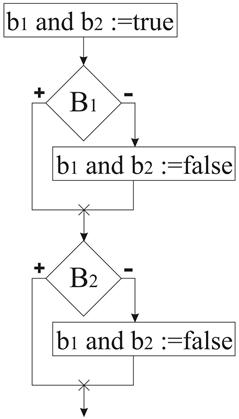
Эти 2 определения блок-схем не эквивалентны, если рассматривать неопределенное значение переменных.

b₁=false b₂=0.

Вторая блок-схема соответствует классическому определению конъюнкции: если хотя бы один из элементов функции не определен, то и функция не определена.

Вариант «а» дает так называемое быстрое означивание конъюнкции. Строго говоря, это другая, отличная от конъюнкции операция, которая часто обозначается “cand” или условный (conditional and, но не в паскале). В паскале обозначение and используется для обеих операций. Точная семантика реализуется директивой компилятора.

В) Предикат в программировании — функция, принимающая один или более аргументов и возвращающая значения булева типа.

(По бухараеву). Предикат – функция на состояниях, имеющая всего лишь два значения, которые в программе обычно обозначаются true и false.

В языках блок-схем предикаты записываются в виде ромбиков, операторы – в виде прямоугольников.

Логические операции

Конъюнкцией двух предикатов A(x) и B(x) называется новый предикат 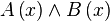, который принимает значение «истина» при тех и только тех значениях х из Т, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях. Множеством истинности Т предиката 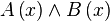является пересечение множеств истинности предикатов A(x) — T1 и B(x) — T2, то есть T = T1 ∩ T2. Например: A(x): «x — чётное число», B(x): «x кратно 3». A(x) B(x) — «x — чётное число и x кратно 3». То есть предикат «x делится на 6».

Дизъюнкцией двух предикатов A(x) и B(x) называется новый предикат 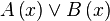, который принимает значение «ложь» при тех и только тех значениях x из T, при которых каждый из предикатов принимает значение «ложь» и принимает значение «истина» во всех остальных случаях. Областью истинности предиката 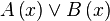является объединение областей истинности предикатов A(x) и B(x).

Отрицанием предиката A(x) называется новый предикат, который принимает значение «истина» при всех значениях x из T, при которых предикат A(x) принимает значение «ложь», если A(x) принимает значение «истина».

Множеством истинности предиката x X является дополнение T' к множеству T в множестве X.

Импликацией предикатов A(x) и B(x) называется новый предикат 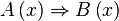, который является ложным при тех и только тех значениях x из T, при которых A(x) принимает значение «истина», а B(x) — значение «ложь», и принимает значение «истина» во всех остальных случаях. Читают: «Если A(x), то B(x)».

С) Написание достаточно сложных условий само по себе требует некоторой системы.

Метод последовательной детализации задачи («сверху-вниз») состоит в том, что исходная сложная задача разбивается на подзадачи. Каждая из подзадач рассматривается и решается отдельно. Если какие-либо из подзадач сложны, они также разбиваются на подзадачи. Процесс продолжается до тех пор, пока подзадачи не сведутся к элементарным. Решения отдельных подзадач затем собираются в единый алгоритм решения исходной задачи. Метод широко используется, так как позволяет вести разработку общего алгоритма одновременно нескольким программистам, решающим локальные подзадачи. Это необходимое условие быстрой разработки программных продуктов.

Д) Сборочный метод(«снизу-вверх») заключается в создании множества программных модулей, реализующих решение типичных задач. При решении сложной задачи программист может использовать разработанные модули в качестве вспомогательных алгоритмов (процедур). Во многих системах программирования уже существуют подобные наборы модулей, что существенно упрощает и ускоряет создание сложного алгоритма.

Е) 1. Квантор общности.

Пусть имеется предикат Р(х) определенный на множестве М

Символ 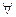называют квантором всеобщности (общности). Это перевернутая первая буква английского слова All- все. Читают «все», «каждый», «любой», «всякий». Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании же 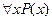х называют связанной квантором всеобщности.

Пример №1: Р(х) – «Простое число х нечетно»

Добавим квантор общности 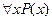– «Всякое простое число х нечетно» - ложное высказывание.

Под выражением 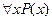понимают высказывание истинное, когда Р(х) истинно для каждого элемента х из множества М и ложное в противном случае. Это высказывание уже не зависит от х.

2. Квантор существования.

Пусть P(x) -предикат определенный на множестве М. Под выражением 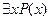понимают высказывание, которое является истинным, если существует элемент 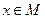, для которого P(x) истинно, и ложным – в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение звучит так: “Существует x, при котором P(x) истинно.” Символ 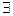называютквантором существования. В высказывании 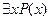переменная x связана этим квантором (на нее навешен квантор)

Вопрос 10

Массивы

A:array[I] of T , где Т произвольный тип (в стандарте, кроме файлов). I – произвольный конечный порядковый тип.

Как значения табличных функций

i
x

X[i] := (Значение X[i]); (Значение X[i]) – определяет функцию в точке;

X[i] := - переопределяет функцию в точке;

Массив (в некоторых языках программирования также таблица, ряд, матрица) — тип или структура данных в виде набора компонентов (элементов массива), расположенных в памяти непосредственно друг за другом. При этом доступ к отдельным элементам массива осуществляется с помощью индексации, то есть ссылки на массив с указанием номера (индекса) нужного элемента. За счёт этого, в отличие от списка, массив является структурой с произвольным доступом.

Семантика:

Множество значений:

1. частный случай: тип индексов I есть ограничение целого типа [1..n], [0..n]. В этом случае множество значений – класс всех последовательностей фиксированной длины n. Тип «массив» - статический; f: N®T, т.е. функций из интервала [1,n] 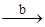T

2. В общем случае значениями являются функции. f: I®T. I – не интервал, из I в T все функции на конечном множестве аргументов. Массив – таблично зависимая функция.

Операции над массивами

Единственное, что можно делать с массивами – вычислять их значения (как функции) по аргументу-индексу (вычисление значения функции в точке). A[e] – A – имя массива, e – любое выражение типа I (a[e]=app(a,e) от двух переменных). Соответствующий оператор называется оператором аппликации, применения функции к аргументу.

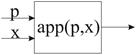
Расширенный синтаксис (Пример использования нечисловых индексных типов)

Т – произвольный тип.

array[I₁] of array [I₂] of T

в этом случае допустим более компактный синтаксис.

array[I₁,…,I_n] of T; a[c₁,…,c_n];

Обычно такой случай связывается с матрицами размерности n.

Задача: подсчитать частоту вхождений каждой малой буквы в заданный текст.

Вычисляется функция: область определения – символы [‘a’, …, ‘s’], область значения – N (натуральные числа).

{k_i – количество вхождений i-ой буквы алфавита}

assign(f,’…’);

reset(f);

for c:=’a’ to ‘z’ do k[c]:=0;

while not eof(f) do

begin

read(f,c);

k[c]:=k[c]+1;

end;

close(f);

Поиск в упорядоченном файле (пример сравнения - массивов и файлов)

Found:=

a_i=x

$ iÎ[1,len(a)] (a_i>=x)

Идея: достаточно найти первое i, такое что x<=a_i, тогда found:=true Û x=a_i, если таковое существует; если такового нет, то found:=false.

Итак, поиск такого первого i: a_i>=x

found1:=$i (a_i>=x)

assign(f,’…’);

reset(f);

found1:=false;

while (not found1) and (not eof(f)) do

begin

read(f,a);

if a>=x then found1:=true

end;

if found1 then found:=a=x

else found:=false;

Дихотомический поиск в упорядоченном массиве (пример сравнения - массивов и файлов )

Program Binar;

Var a:array[1..n] of integer;

l,r,m:integer;

found:boolean;

Begin

{ввод a}

l:=1;

r:=n;

found:=false;

while (l<=r) and not found do

begin

m:=(l+r) div 2;

if a[m]=x

then found:=true

else if a[m]<x then l:=m+1

else r:=m-1;

end;

end.

Вопрос 11

Упорядоченные массивы.

(Интернет){

Упорядоченный массив — массив состоящий из последовательности данных расположенных по возрастанию.}

(Даша) {

Упорядоченный массив — упорядоченный набор данных согласно}

Паскаль не использует явно понятие упорядоченного типа, хотя в математическом или абстрактном смысле они представляют собой тип данных с явно выраженным набором операций.

Для любого i Î [1,length(a)] (ai<=ai+1)

Для любого i,j Î [1,length(a)] (i<=j → ai<=aj)

Упорядоченность используется в программировании для создания более эффективных алгоритмов решения задач, в первую очередь задач поиска.

Дихотомический поиск.

(Интернет) {

Дихотомический поиск - Метод быстрого поиска, при котором упорядоченный набор данных (список) разделяется на две части и операция сравнения всегда выполняется для среднего элемента списка: после сравнения одна половина списка отбрасывается и операция выполняется для оставшейся половины и т.д. }

Дихотомический поиск в упорядоченном массиве

Program Binar;

Var a:array[1..n] of integer;

l,r,m:integer;

found:boolean;

Begin

{ввод a}

l:=1;

r:=n;

found:=false;

while (l<=r) and not found do

begin

m:=(l+r) div 2;

if a[m]=x

then found:=true

else if a[m]<x then l:=m+1

else r:=m-1;

end;

end.

{Текст программы взят из книги, а не с лекции, но большой разницы быть не должно, т.к. алгоритм один}

Операции над упорядоченными массивами (определение).

(Даша){

Операции - замена, перестановка,сортировка(?), поиск. }

(Интернет) {

Проверка на включение, поиск элемента, объединение, пересечение, разность, симметрическая разность}

Вопрос 12