Программирование алгоритмов циклической структуры.

Цель работы:изучить операторы цикла и приобрести практическиенавыки в программировании алгоритмов циклической структуры.

Задание

1. Изучить операторы цикла языка Бейсик и особенности их при-

менения.

2. Для заданного варианта составить схему алгоритма циклической структуры и реализующие его программы с использованием условного опе-ратора и операторов цикла.

3. Произвести на ЭВМ расчеты по разработанным программам для исходных данных, приведенных в табл. 4.1, и сравнить результаты расчетов.

4. Получить распечатки программ и результатов расчета.

5. Оформить отчет по лабораторной работе.

Указания по выполнению работы

Алгоритм циклической структуры включает в себя одну из основных структур - цикл, который бывает двух типов: цикл До и цикл Пока (рис.4.1). В цикле До тело цикла выполняется до проверки некоторого условия “да” - ус-ловие истинно, “нет ” - условие ложно. Телом цикла называется последова-тельность действий, выполняемых в цикле многократно. В цикле Пока про-верка условия производится до выполнения тела цикла.

При программировании алгоритмов циклической структуры следует иметь в виду, что в цикле Пока при истинности условия, тело цикла не вы-полняется ни разу, а в цикле До оно всегда выполняется хотя бы один раз, независимо от условия. Цикл До рекомендуется использовать в задачах с за-ранее известным числом повторений цикла, цикл Пока - когда число повто-рений цикла заранее неизвестно, например, в расчетах до получения резуль-тата с заданной точностью.

Организация циклов в программах может осуществляться с помощью условного оператора (рис.4.1), рассмотренного в лабораторной работе № 3. или специальных операторов цикла.

Оператор цикла F0R-NEXT.

Оператор F0R-NEXT позволяет организовать выполнение блока опе-раторов определенное количество раз. Оператор F0R-NEXT имеет сле-дующую форму:

FOR счетчик = начало TO конец [STEP шаг] [операторы цикла]

[EXIT FOR] [операторы цикла] NEXT счетчик,

где счетчик – числовая переменная, используемая как счетчик цикла; начало – начальное значение счетчика; конец – конечное значение счетчика; шаг – шаг изменения значения счетчика по умолчанию равен 1; операторы цикла – набор операторов предназначенных для повторения.

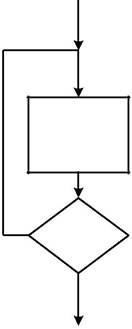
Тело цикла

^Да Условие

Нет

а)

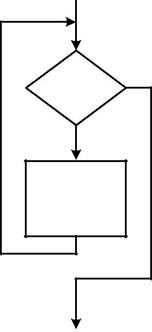
Да

Условие

Нет

Тело цикла

1. Операторы тела цикла

2. Если <Условие> выполняется перейти к п.1

3. ….

1. Если <Условие> выполняется перейти к п.4

2. Операторы тела цикла

3. Переход к п.1

4. …

б)

Рис.4.1. Виды циклов и их программирование с использованием ус-ловного оператора IF:

а - структура цикла До; б - структура цикла Пока.

Цикл F0R-NEXT выполняется до тех пор, пока текущее значение счет-чика не превышает его конечного его конечного значения. При завершении текущего цикла к значению счетчика прибавляется значение шага. Если конец

меньше начала, то шаг должен быть отрицательным. Если начало и конец имеют одно и тоже значение то цикл выполняется один раз вне зависимости от значения шага.

В качестве примера на рис.4.2 приведены алгоритм и программа вы-числения факториала Р = n! с оператором FOR-NEXT.

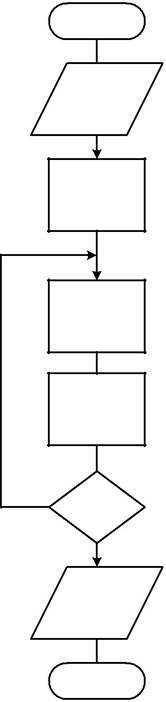
Начало

Ввод n

P=1

i=1

P=P*i

i=i+1

^Да i<=n

Нет

Вывод

Y

Конец

а)

REM Программа вычисления n! REM с применением оператора цикла PRINT “Введите значение n=”; INPUT N

P=1

FOR I=1 TO N P=P*I

NEXT I

PRINT “Значение ”; N;”!=”;P END

б)

Рис.4.2. Пример программирования циклического алгоритма:

а - схема алгоритма; б - его программная реализация с

применением операторов цикла

F0R-NEXT.

Решение приведенной задачи сводится к организации цикла, при каж-дом прохождении которого значение произведения Р умножается на очеред-ной сомножитель i. До входа в цикл необходимо задать Р=1. Для организации цикла в программах используется переменная I. При превышении этой пере-менной значения N происходит выход из цикла и вывод результатов расчета на дисплей.

Таблица 4.1

Варианты заданий к лабораторной работе № 4

№	Составить программу табулирования функции y на	Исходные данные
п.п.			отрезке [a,b] с шагом h			a	b	h
1.	y = x /( x2+1)					4,0	6,0	0,2
2.	y = x /( x3+1)					3,0	5,0	0,25
3.	y =	x / x3					1,0	10,0	1,0
4.	y = x ln x2					2,5	3,5	0,1
5.	y =ln( x +1) /( x2+1)					2,0	6,0	0,5
6.	y = e x /( x2+2)					1,2	2,1	0,1
7.	y =2sin2 x /(1+ x3)						3,14	0,31
8.	y =cos x /(1+ x3)					1,57	3,14	0,16
9.	y =5sin x /(1+ x2)					4,3	5,5	0,2
	y =(1−cos2 x ) /(0,5 x +1)					1,5	2,5	0,1
	Составить программу вычисления k членов последовательности
№		Формула общего члена	k	№	Формула общего члена	k
п.п					п.п
11.	ak	= k 2 /( k 3 +2)		12.	ak	= ( k 2 +10) / 2k
13.	a k	=	k /( k +1)		14.	a k	= k /( k 2 +2)
15.	ak	= (2 k +1) / k 2		16.	ak	= k k −1 /( k +5)
	Составить программу вычисления суммы k членов последовательности
№		Формула общего члена	k	№	Формула общего члена	k
п.п					п.п
17.	a k	=	k /( k +3)		18.	ak	= ( k +1) / k 2
19.	ak	= k 2 /( k 2 +5)		20.	ak	= k 2 /( k 3 +1)
21.	ak	= k 2 / 2k		22.	ak	= (5k +3) / ek

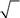
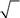
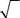Составить программу вычисления произведения k членов последовательности

№		Формула общего члена	k	№	Формула общего члена	k
п.п				п.п
23.	ak	= k 3 /( k +1)		24.	ak =(2 k +1)	/ 5k 2
25.	ak	= (2 k +1) / k 3		26.	ak =(2 k +1)	/ k 3
27.	ak	= k /(2 k +1)		28.	ak =5k /( ek +1)
29.	a k	= k /( k 3 −1)		30.	ak = e k /(3k 2+1)

Лабораторная работа №5