Порядок выполнения лабораторной работы. Исходными данными для данной лабораторной работы являются результаты статистической обработки текста

Исходными данными для данной лабораторной работы являются результаты статистической обработки текста, выполненной в предыдущей лабораторной работе. Из лабораторной работы «Определение количества информации, содержащегося в сообщении» для данной работы необходимо взять:

1) список символов данного текста;

2) оценку вероятностей появления символов в тексте;

3) значение энтропии источника.

Расчеты рекомендуется выполнять в табличной форме, используя MS Excel.

1. Отсортировать символы в порядке убывания их вероятности появления в тексте.

2. Построить один из возможных вариантов по правилу Шеннона-Фано для посимвольного кодирования заданного текста.

3. Определить энтропию и среднее количество двоичных разрядов, необходимых для передачи текста при использовании эффективных кодов.

4. Проверить возможность однозначного декодирования полученных кодов, рассмотрев пример передачи слова, состоящего из не менее 10 символов.

Содержание отчёта

1. Название и цель работы.

2. Заполненная таблица для 50-ти символов, содержащая:

Ø список символов;

Ø значения вероятностей;

Ø кодовые комбинации;

Ø ступени деления.

3. Значение средней информации в битах.

4. Описание применяемых формул.

5. Составленное сообщение, содержащее не менее 10 символов и кодовая строка.

6. Описание декодирования данного сообщения любым способом.

7. Выводы по работе соответственно цели лабораторной работы.

Приложение к лабораторной работе «Кодирование дискретных источников информации методом Шеннона-Фано»

Основные положения

При кодировании дискретных источников информации часто решается задача уменьшения избыточности, т.е. уменьшения количества символов, используемых для передачи сообщения по каналу связи. Это позволяет повысить скорость передачи за счет уменьшения количества передаваемой информации, а точнее, за счет отсутствия необходимости передачи избыточной информации. В системах хранения уменьшение избыточности позволяет снизить требования к информационной емкости используемой памяти.

Для передачи и хранения информации, как правило, используется двоичное кодирование. Любое сообщение передается в виде различных комбинаций двух элементарных сигналов. Эти сигналы удобно обозначать символами 0 и 1. Тогда кодовое слово будет состоять из последовательностей нулей и единиц.

Если алфавит A состоит из N символов, то для их двоичного кодирования необходимо слово разрядностью n, которая определяется

n = élog₂ Nù .

Это справедливо при использовании стандартных кодовых таблиц, например, ASCII, KOI-8 и т.п., обеспечивающих кодирование до 256 символов.

Если в используемом алфавите символов меньше, чем используется в стандартной кодовой таблице, то возможно использование некоторой другой таблицы кодирования, позволяющей уменьшить количество двоичных разрядов, используемых для кодирования любого символа. Это, в определенном смысле, обеспечивает сжатие информации.

Например, если необходимо передавать или хранить сообщение, состоящее из символов кириллицы, цифр и семи символов разделителей {«.», «,», «:», «;», «!», « кавычки », «?»} ( всего 50 символов), мы можем воспользоваться способами кодирования:

Ø Кодировать каждый символ в соответствии со стандартной кодовой таблицей, например, KOI-8R. По этой таблице каждый символ будет представляться 8 битовым (байт) кодовым словом, n₁ = 8;

Ø Составить и использовать отдельную кодовую таблицу, это может быть некоторый усеченный вариант стандартной таблицы, не учитывающую возможность кодирования символов, не входящих в передаваемое сообщение, тогда необходимый размер кодового слова

n₂ =élog₂ Nù== é log₂ 50ù=6.

Очевидно, передача сообщения с помощью такого кода будет более эффективной, т.к. будет требовать меньшего количества бинарных сигналов при кодировании. Можно говорить о том, что при таком кодировании мы не передаем избыточную информацию, которая была бы в восьмибитовом кодировании;

Ø Использовать специальный код со словом переменной длины, в котором символы, появляющиеся в сообщении с наибольшей вероятностью, будут закодированы короткими словами, а наименее вероятным символам сопоставлять длинные кодовые комбинации. Такое кодирование называется эффективным.

Эффективное кодирование базируется на основной теореме Шеннона для каналов без шума, в которой доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.

Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каждый элементарный сигнал должен принимать значения 0 и 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.

При отсутствии статистической взаимосвязи между кодируемыми символами конструктивные методы построения эффективных кодов были даны впервые К.Шенноном и Н.Фано. Их методики существенно не различаются, поэтому соответствующий код получил название кода Шеннона-Фано.

Код строится следующим образом:

буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним — 0. Каждая из полученных групп, в свою очередь, разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.

Рассмотрим алфавит из восьми букв (табл. 1). Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется n₂ =3символа. В табл.1 приведен один из возможных вариантов кодирования по сформулированному выше правилу.

Таблица 1
Символы	Вероятности p(ai)	Кодовые комбинации	1 ступень	2 ступень	3 ступень	4 ступень	ступень
a1	0.22
a2	0.20
a3	0.16
a4	0.16
a5	0.10
a6	0.10
a7	0.04
a8	0.02

Очевидно, для указанных вероятностей можно выбрать другое разбиение на подмножества не нарушая алгоритма Шеннона-Фано. Такой пример приведен в табл.2.

Таблица 2
Символы	Вероятности p(ai)	Кодовые комбинации	1 ступень	2 ступень	3 ступень	4 ступень	ступень
a1	0.22
a2	0.20
a3	0.16
a4	0.16
a5	0.10
a6	0.10
a7	0.04
a8	0.02

Сравнивая приведенные таблицы, обратим внимание на то, что по эффективности полученные коды различны. Действительно, в табл.2 менее вероятный символ a₄ будет закодирован двухразрядным двоичным числом, в то время как a₂ , вероятность появления которого в сообщении выше, кодируется трехразрядным числом.

Таким образом, рассмотренный алгоритм Шеннона-Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу.

Энтропия набора символов в рассматриваемом случае определяется как

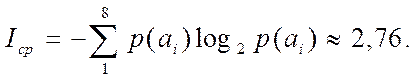
Напомним, что смысл энтропии в данном случае, как следует из теоремы Шеннона, — наименьшее возможное среднее количество двоичных разрядов, необходимых для кодирования символов алфавита размера восемь с известными вероятностями появления символов в сообщении.

Мы можем вычислить среднее количество двоичных разрядов, используемых при кодировании символов по алгоритму Шеннона-Фано

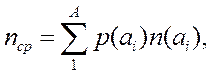
где: A — размер (или объем) алфавита, используемого для передачи сообщения;

n(a_i) — число двоичных разрядов в кодовой комбинации, соответствующей символу a_i.

Таким образом, мы получим для табл.1 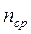=2,84, а для табл.2 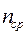=2,80. Построенный код весьма близок к наилучшему эффективному коду по Шеннону, но не является оптимальным. Должен существовать некоторый алгоритм позволяющий выполнить большее сжатие сообщения.