Абораторная работа №3. Исследование пространственных преобразований графических объектов.

Целью работы являетсязакрепление на практике знаний математического аппарата, положенного в основу пространственных преобразований графических объектов (на примере преобразований четырехгранников).

Теоретическая справка.При пространственных преобразованиях графических объектов каждая точка P(x,y,z) в пространстве однозначно отображается содержащей однородные координаты этой точки матрицей (координатным вектором) размером 1´4 вида 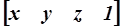. Отрезку прямой между точками (x₁, y₁ ,z₁) и (x ₂ , y₂ ,z₂) ставится в соответствие 2´4 матрица вида 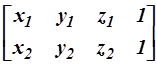. Многогранник может быть представлен M´4 матрицей (где M – число вершин многогранника), содержащей однородные координаты его вершин: 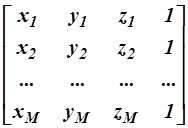. Преобразования осуществляются путем умножения таких матриц на матрицу общего преобразования размером 4´4 вида 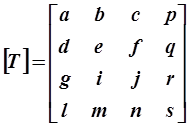. Результат преобразования зависит от конкретного вида матрицы преобразования. Если координатный вектор преобразованной точки 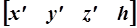содержит h ≠ 1 и h ≠ 0, результат нормализуют путем деления всех четырех составляющих однородных координат на h, т.е. приводят к виду 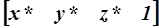, где x* = x¢/h, y* = y¢/h, z* = z¢/h. Равенство нулю координаты h в результате матричного умножения (координатный вектор преобразованной точки при этом имеет вид 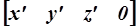) свидетельствует о том, что исходная точка преобразована в точку бесконечности, лежащую на луче, который идет из начала координат через точку (x¢,y¢,z¢).

Матрицы простых пространственных преобразований графических объектов представлены в приложении 2.

Рекомендации по выполнению лабораторной работы:

Ряд последовательных преобразований объекта можно комбинировать: предварительно рассчитав матрицу полного преобразования путем перемножения в строгой последовательности матриц отдельных преобразований, применить ее для преобразования исходного объекта.

1. Согласуйте с ведущим преподавателем номер варианта, в соответствии с которым вы будете проводить исследования. Варианты заданий представлены в таблице 2. Ознакомьтесь с данным вариантом задания (с рекомендуемыми значениями координат вершин исходного четырёхгранника и – при выполнении соответствующих пунктов программы – коэффициентов матрицы общего преобразования или иных параметров преобразования).

2. Осуществите следующие преобразования исходного четырехгранника, удаляя каждый раз перед очередным преобразованием результат предыдущего^[2]:

a) локальное масштабирование по координатным осям x и z, используя одну матричную операцию;

b) симметричное отражение относительно координатной плоскости xz (y = 0);

c) симметричное отражение относительно оси x;

d) сдвиг вдоль оси x пропорционально координате z;

e) поворот на – 90° вокруг координатной оси z;

f) поворот на угол f вокруг координатной оси y.

Сформулируйте вывод относительно назначения коэффициентов левой верхней 3´3 подматрицы матрицы общего преобразования.

3. Осуществите перемещения исходного четырехгранника вдоль осей y и z, используя одну матричную операцию.

Сформулируйте вывод относительно назначения коэффициентов левой нижней 1´3 подматрицы матрицы общего преобразования.

4. Реализуйте по отношению к исходному четырехграннику проецирование в однородных координатах.

Сделайте выводы о математическом смысле проведенного преобразования и процедуры нормализации результата умножения матриц. Сформулируйте также вывод относительно назначения коэффициентов правой верхней 3´1 подматрицы матрицы общего преобразования.

5. Реализуйте общее масштабирование исходного четырехгранника.

Сформулируйте вывод относительно назначения коэффициента правой нижней 1´1 подматрицы матрицы общего преобразования.

6. Осуществите поворот исходного четырехгранника на угол f вокруг прямой линии, параллельной координатной оси y и заданной, соответственно, значениями двух координат: x = l, z = n; используйте при этом следующие последовательные преобразования:

a) переместите объект преобразования таким образом, чтобы прямая, относительно которой совершается поворот, совпала с осью y;

b) поверните объект на требуемый угол вокруг оси y;

c) осуществите обратное (по отношению к п/п. a) перемещение объекта.

7. Рассчитайте матрицу полного преобразования, реализованного в предыдущем пункте. Примените ее для преобразования исходного четырехгранника. Сравните результаты, полученные в настоящем и предыдущем пунктах.

8. Осуществите поворот исходного четырехгранника на угол χ вокруг прямой линии, которая заданна точкой с координатами (0, 0, 0) и направляющим вектором, представленным матрицей 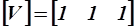; используйте при этом следующие последовательные преобразования:

a) поверните объект преобразования вокруг двух координатных осей на соответствующие углы таким образом, чтобы прямая, относительно которой совершается поворот, совпала с какой-либо координатной осью;

b) реализуйте поворот на требуемый угол вокруг той координатной оси, с которой в п/п. a совмещена прямая;

c) осуществите обратные (по отношению к п/п. a) повороты в обратной же последовательности.

9. Реализуйте симметричное отражение исходного четырехгранника относительно плоскости 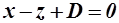, используя при этом следующие последовательные преобразования:

a) определив координаты какой-либо одной точки, принадлежащей плоскости отражения, переместите объект преобразования так, чтобы эта точка попала в начало координат;

b) поверните объект вокруг одной или двух координатных осей таким образом, чтобы плоскость отражения совпала с какой-либо координатной плоскостью;

c) симметрично отразите объект относительно той координатной плоскости, с которой в п/п. b совмещена плоскость отражения;

d) осуществите соответственно один или два обратных (по отношению к п/п. b) поворота (во втором случае – в обратной же последовательности);

e) осуществите обратное (по отношению к п/п. a) перемещение объекта.

По результатам выполнения пунктов 6, 7, 8 и 9 сформулируйте вывод о возможных путях реализации комбинаций пространственных преобразований.

10. Получите такую ортографическую проекцию исходного четырехгранника на плоскость xy (z = 0), в которой какая-либо грань объекта, не параллельная ни одной координатной плоскости, была бы отражена без искажения.

Сформулируйте вывод относительно возможности применения ортографического проецирования для формирования вспомогательных видов и сечений геометрически сложных трехмерных объектов с целью адекватного восприятия их формы.

Таблица 2.

Дисциплина: «Компьютерная графика»
Лабораторная работа №3 Вариант задания №1
Координаты вершин исходного четырёхгранника
x1 = 100; y1 = 100; z1 = 50;x2 = 0; y2 = 100;z2 = 150; x3 = 100; y3 = 0; z3 = 150;x4 = 100; y4 = 100; z4 = 150
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 3; j = 1.5*
2d	g = 1.5*
2f	f = 30°
	m = 100; n = 150*
	p = 0.03; q = 0.02*
	s = 2*
	f = 50°; l = 100; n = 50*
	χ = 105°
	D = -50
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)

______________________________________

Дисциплина: «Компьютерная графика»
Лабораторная работа №3 Вариант задания №2
Координаты вершин исходного четырёхгранника
x1 = 200; y1 = 100; z1= 200;x2 = 200; y2 = 250; z2= 100; x3 = 100; y3 = 250; z3= 200;x4 = 200; y4 = 250; z4 = 200
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 0.5; j = 1.5 *
2d	g = -0.5*
2f	f = 120°
	m = 150; n = 100 *
	p = 0.003;r = 0.001 *
	s = 0.5*
	f = 140°; l = 100; n = 100*
	χ = 80°
	D = 100
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)
Дисциплина: «Компьютерная графика»
Лабораторная работа №3 Вариант задания №3
Координаты вершин исходного четырёхгранника
x1 = 100;y1 = 250; z1= 50;x2 = 100; y2 = 250; z2= 250; x3 = 200;y3 = 150; z3= 150; x4 = 200; y4 = 250; z4 = 150
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 2.1; j = 1.2*
2d	g = 1.3*
2f	f = 45°
	m = 50; n = 300 *
	q = 0.01;r = 0.02*
	s = 3*
	f = 80°; l = 300; n = 150*
	χ = 100°
	D = 200
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)

______________________________________

Дисциплина: «Компьютерная графика»
Лабораторная работа №3 Вариант задания №4
Координаты вершин исходного четырёхгранника
x1 = 100; y1 = 150;z1= 300;x2 = 200; y2 = 150; z2= 200; x3 = 100; y3 = 50; z3= 200;x4 = 100; y4 = 150; z4 = 200
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 1.6; j = 1.2*
2d	g = 1.1*
2f	f = 90°
	m = 50; n = -100*
	p =0.002;q = 0.001;r = 0.003*
	s = 0.6 *
	f = 115°;l = 150;n = 150*
	χ = 130°
	D = -150
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)
Дисциплина: «Компьютерная графика»
Лабораторная работа №3 Вариант задания №5
Координаты вершин исходного четырёхгранника
x1 = -200; y1 = -200;z1= 0;x2 = -100;y2 = -200; z2= 100; x3 = -200;y3 = -100; z3= 100;x4 = -200; y4 = -200; z4 = 100
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 0.5; j = 0.8*
2d	g = 1.2*
2f	f = 30°
	m = 300; n = 100*
	q = 0.002*
	s = 1.5*
	f = 15°;l = 200;n = 100*
	χ = 160°
	D = -200
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)

______________________________________

Дисциплина: «Компьютерная графика»
Лабораторная работа №3 Вариант задания №6
Координаты вершин исходного четырёхгранника
x1 = -100; y1 = -100; z1= -300;x2 = +200;y2 = -100; z2= -200; x3 = -100; y3 = -200; z3= -200;x4 = -100; y4 = -100; z4 = -200
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 0.4; j = 1.3*
2d	g = 0.5*
2f	f = 60°
	m = 300; n = 400*
	r = 0.008*
	s = 1.8*
	f = 250°;l = -400;n = -300*
	χ = 210°
	D = 130
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)