Параллельная сортировка Бэтчера
Чтобы получить алгоритм обменной сортировки, время работы которого имеет порядок, меньший O(n2), необходимо подобрать для сравнений пары несоседних ключей (Ki, Kj); иначе придется выполнить столько операций обмена записей, сколько инверсий имеется в исходной перестановке. В 1964 году К. Э. Бэтчер открыл интересный способ программирования последовательности сравнений, предназначенной для поиска возможных обменов. Его метод далеко не очевиден.
Схема сортировки Бэтчера несколько напоминает сортировку Шелла, но сравнения выполняются по-новому, а потому цепочки операций обмена записей не возникает. Бэтчера действует, как 8-, 4-, 2- и 1-сортировка, но сравнения не перекрываются. Поскольку в алгоритме Бэтчера, по существу, происходит слияние пар рассортированных подпоследовательностей, его можно назвать обменной сортировкой со слиянием. Схема метода представлена на рис. 26.
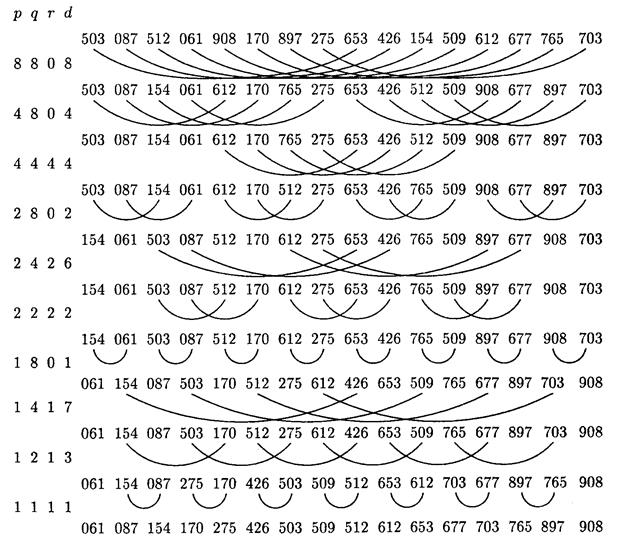
Рис. 26. Обменная сортировка со слиянием (метод Бэтчера)
Ниже представлена схема алгоритма. Здесь t=[logN] (целая часть числа). Переменная d имеет смысл шага сортировки, то есть сравниваются ключи K[i] и K[i+d]. Символом “<->” обозначена операция обмена значений двух переменных.
К сожалению, количество вспомогательных операций, необходимых для управления последовательностью сравнений в методе Бэтчера, весьма велико, так что программа в итоге становится менее эффективна, чем многие другие рассмотренные выше методы. Однако она обладает одним важным компенсирующим качеством: все сравнения и/или обмены можно выполнять одновременно на компьютерах или в сетях, которые реализуют параллельные вычисления. С такими параллельными операциями сортировка осуществляется за [lgN]([lgN] + 1)/2 шагов, и это один из самых быстрых общих методов среди всех известных. Например, 1024 элемента можно рассортировать методом Бэтчера всего за 55 параллельных шагов.
T-1
p = 2
T-1
╔═>q = 2 ; r=0; d=p;
║
║ ╔═══<════════════════════════════════════<══════╗
║ for i=0 to N-d-1 таких, что i&p = r; ║
║ ┌────────────────────────────────────────┐ ║
║ │if(K[i+1] > K[i+d+1]) K[i+1]<->K[i+d+1] │ ║
║ └────────────────────────────────────────┘ ║
║ if(q=p) ║
║ then ║ else ║
║ ╔════<════╩════>═════════════════════════╗ ║
║ ║ ║ ║
║ p=[p/2];(деление нацело) d=q-p; ║
║ if(p<=0) Конец алгоритма; q=q/2; ║
║ else═>╗ r=p; ║
╚═══════╝ ╚═══>══╝
Алгоритм сортировки Бетчера
Быстрая сортировка
Алгоритм быстрой сортировки был разработан более 40 лет назад, однако в настоящее время является, пожалуй, наиболее широко применяемым и одним их самых эффективных алгоритмов.
Метод основан на подходе "разделяй-и-властвуй". Общая схема такова:
1. из массива выбирается некоторый опорный элемент a[i],
2. запускается процедура разделения массива, которая перемещает все ключи, меньшие, либо равные a[i], влево от него, а все ключи, большие, либо равные a[i] – вправо. В результате выполнения данной операции массив будет состоять из двух подмножеств, причем левое меньше либо равно правого:
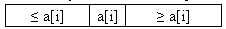 .
.
3. для обоих подмассивов проверяется условие: если хотя бы в одном из них содержится более двух элементов, то для него рекурсивно запускается та же процедура.
В среднем производительность метода составляет O(N log N) операций. Однако при определенных входных данных она падает до O(n2) операций. Такое происходит, если каждый раз в качестве опорного элемента выбирается максимум или минимум входной последовательности.
