Рекуррентные соотношения (например, вычисление чисел Фиббоначи и др.)
При решении многих комбинаторных задач пользуются методом сведения данной задачи к задаче, касающейся меньшего числа предметов. Метод сведения к аналогичной задаче для меньшего числа предметов называется методом рекуррентных соотношений (от латинского "recurrere" - "возвращаться").
Понятие рекуррентных соотношений проиллюстрируем классической проблемой, которая была поставлена около 1202 года Леонардо из Пизы, известным как Фибоначчи. Важность чисел Фибоначчи для анализа комбинаторных алгоритмов делает этот пример весьма подходящим.
Фибоначчи поставил задачу в форме рассказа о скорости роста популяции кроликов при следующих предположениях. Все начинается с одной пары кроликов. Каждая пара становится фертильной через месяц, после чего каждая пара рождает новую пару кроликов каждый месяц. Кролики никогда не умирают, и их воспроизводство никогда не прекращается.
Пусть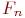 
- число пар кроликов в популяции по прошествии 
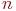месяцев, и пусть эта популяция состоит из 
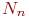пар приплода и 
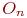"старых" пар, то есть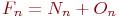 
Таким образом, в очередном месяце произойдут следующие события: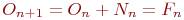 
Старая популяция в 
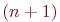-й момент увеличится на число родившихся в момент времени . 
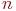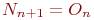Каждая старая пара в момент времени 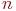производит пару приплода в момент времени 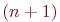В последующий месяц эта картина повторяется: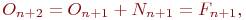 
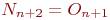
Объединяя эти равенства, получим следующее рекуррентное соотношение:
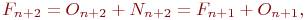
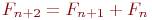
Выбор начальных условий для последовательности чисел Фибоначчи не важен; существенное свойство этой последовательности определяется рекуррентным соотношением. Будем предполагать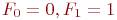 
(иногда 
).
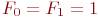Рассмотрим эту задачу немного иначе.
Пара кроликов приносит раз в месяц приплод из двух крольчат (самки и самца), причем новорожденные крольчата через два месяца после рождения уже приносят приплод. Сколько кроликов появится через год, если в начале года была одна пара кроликов?
Из условия задачи следует, что через месяц будет две пары кроликов. Через два месяца приплод даст только первая пара кроликов, и получится 3 пары. А еще через месяц приплод дадут и исходная пара кроликов, и пара кроликов, появившаяся два месяца тому назад. Поэтому всего будет 5 пар кроликов. Обозначим через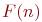 
количество пар кроликов по истечении 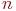месяцев с начала года. Ясно, что через 
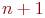месяцев будут эти 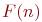пар и еще столько новорожденных пар кроликов, сколько было в конце месяца
, то есть еще 
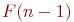пар кроликов. Иными словами, имеет место рекуррентное соотношение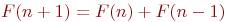 
Так как, по условию,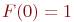 
и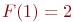 
, то последовательно находим 
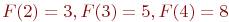и т.д.
В частности,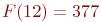 
Числа 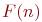называются числами Фибоначчи. Они обладают целым рядом замечательных свойств. Теперь выведем выражение этих чисел через 
.
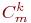Для этого установим связь между числами Фибоначчи и следующей комбинаторной задачей.
Одномерные массивы и алгоритмы работы с ними (нахождение максимального и минимального элементов, суммирование элементов, вставка и удаление элементов, перестановка элементов местами и т.д.)
Массив это структура данных, представленная в виде группы ячеек одного типа, объединенных под одним единым именем. Массивы используются для обработки большого количества однотипных данных. Имя массива является указателем, что такое указатели расскажу немного позже. Отдельная ячейка данных массива называется элементом массива. Элементами массива могут быть данные любого типа. Массивы могут иметь как одно, так и более одного измерений. В зависимости от количества измерений массивы делятся на одномерные массивы, двумерные массивы, трёхмерные массивы и так далее до n-мерного массива. Чаще всего в программировании используются одномерные и двумерные массивы, поэтому мы рассмотрим только эти массивы.
Одномерные массивы в С++:
Одномерный массив - массив, с одним параметром, характеризующим количество элементов одномерного массива. Фактически одномерный массив - это массив, у которого может быть только одна строка, и n-е количество столбцов. Столбцы в одномерном массиве - это элементы массива. На рисунке 1 показана структура целочисленного одномерного массива a. Размер этого массива - 16 ячеек.
Заметьте, что максимальный индекс одномерного массива a равен 15, но размер массива 16 ячеек, потому что нумерация ячеек массива всегда начинается с 0. Индекс ячейки – это целое неотрицательное число, по которому можно обращаться к каждой ячейке массива и выполнять какие-либо действия над ней (ячейкой).