Арифметическое представление функций алгебры логики

Существует много способов задания логических функций. Ранее рассматривали табличный способ, при котором каждому набору значений в таблице истинности указывается значение самой логической функции. Этот способ показателен и может быть применен для записи функций от любого числа переменных, однако при анализе связей функций алгебры логики такая запись не компактна. Проще выглядит аналитическая запись в виде формул.

Рассмотрим фиксированный набор переменных на котором заданна функция алгебры логики, а так как любая переменная, принимающая значения 1 или 0, то набор значений переменных фактически представляет собой некоторое двоичное число. Представим, что номером набора будет некоторое двоичное число i, которое получается:

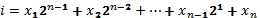
И пусть имеется какая-то f(i) { x₁,x₂,…,x_n } которая равна 0, если номер набора равен 1 и равна 1, если номер набора не равен i

f(i)={		Терм

Дизъюнктивный терм или max терм - это терм, связывающий все переменные, представленные в прямой или инверсионной форме знаком дизъюнкции (константа нуля).

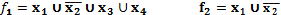
Конъюнктивный терм или min терм – это терм, связывающий переменные представленные в прямой или инверсионной форме знаком конъюнкции(константа единицы)

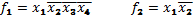R=4	R=2

R – ранг терма, определяется количеством переменных, входящих в данный терм.

На основании вышесказанного можно сформулировать теоремы:

1) Любая таблично заданная функция алгебры логики может быть представлена аналитическим способом в виде:

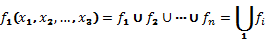
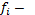номер набора на котором F=1

Н.Д.Ф. (Нормальная дизъюнктивная форма) – объединение термов, включающих min термы переменного ранга.

2) Любая таблично заданная функция алгебры логики может быть представлена аналитическим способом в виде:

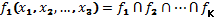
К – количество двоичных наборов при которых F=0

Н.К.Ф. (Нормальная конъюнктивная форма) – объединение термов, включающих в себя max термы различных рангов.

Пример:

Записать в аналитическом виде функцию заданную в таблице:

X1	X2	X3	F(x1,x2,x3)

Н.Д.Ф. F(x₁,x₂,x₃)=F(0,0,0)+F(0,1,1)+f(1,0,0)=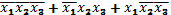

Современный нормальные формы.

Задание функций алгебры логики ранее рассмотренными способами либо громоздко, либо часто неудобно для любых преобразований. Поэтому целесообразно в новой форме представлять следующие требования:

1) Удобство получения

2) Однозначность представления в этой форме любых функций алгебры логики

3) Простота преобразований и упрощений

Всем этим требованиям удовлетворяет С.Н.Д.Ф. и С.Н.К.Ф. С.Н.Ф. отличается от Н.ф. тем, что всегда содержит только термы max ранга и дает однозначное представление функции.