Абораторная работа №2. Исследование двумерных преобразований графических объектов.

Целью работы являетсязакрепление на практике знаний математического аппарата, положенного в основу двумерных преобразований графических объектов (на примере преобразований треугольников).

Теоретическая справка.При двумерных преобразованиях графических объектов каждая точка P(x,y) на плоскости однозначно отображается содержащей однородные координаты этой точки матрицей (координатным вектором) размером 1´3 вида 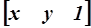. Отрезку прямой между точками (x₁, y₁) и (x ₂ , y₂) ставится в соответствие 2´3 матрица вида 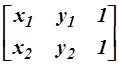. Многоугольник может быть представлен M´3 матрицей (где M – число вершин многоугольника), содержащей однородные координаты его вершин: 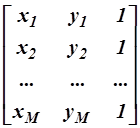. Преобразования осуществляются путем умножения таких матриц на матрицу общего преобразования размером 3´3 вида 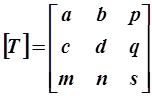. Результат преобразования зависит от конкретного вида матрицы преобразования. Если координатный вектор преобразованной точки 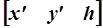содержит h ≠ 1 и h ≠ 0, результат нормализуют путем деления всех трех составляющих однородных координат на h, т.е. приводят к виду 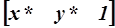, где x* = x¢/h, y* = y¢/h. Равенство нулю координаты h в результате матричного умножения (координатный вектор преобразованной точки при этом имеет вид 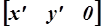) свидетельствует о том, что исходная точка преобразована в точку бесконечности, лежащую на луче, который идет из начала координат через точку (x¢,y¢).

Матрицы простых двумерных преобразований графических объектов представлены в приложении 1.

Ряд последовательных преобразований объекта можно комбинировать: предварительно рассчитав матрицу полного преобразования путем перемножения в строгой последовательности матриц отдельных преобразований, применить ее для преобразования исходного объекта.

Рекомендации по выполнению лабораторной работы:

1. Согласуйте с ведущим преподавателем номер варианта, в соответствии с которым вы будете проводить исследования. Варианты заданий представлены в таблице 1. Ознакомьтесь с данным вариантом задания (с рекомендуемыми значениями координат вершин исходного треугольника и – при выполнении соответствующих пунктов программы – коэффициентов матрицы общего преобразования или иных параметров преобразования).

2. Осуществите следующие преобразования исходного треугольника, удаляя каждый раз перед очередным преобразованием результат предыдущего^[1]:

a) локальное масштабирование по координатным осям x и y, используя одну матричную операцию;

b) симметричное отражение относительно оси x (или y);

c)симметричное отражение относительно точки начала координат (поворот на 180°);

d) сдвиг вдоль оси x пропорционально координате y (или вдоль оси y пропорционально координате x);

e)поворот на 90°(или на – 90°) относительно точки начала координат;

f) поворот на угол q относительно точки начала координат;

g) отражение относительно прямой линии у = x (или у = – x);

Сформулируйте вывод относительно назначения коэффициентов левой верхней 2´2 подматрицы матрицы общего преобразования.

3. Реализуйте перемещения исходного треугольника вдоль координатных осей x и y, используя одну матричную операцию.

Сформулируйте вывод относительно назначения коэффициентов левой нижней 1´2 подматрицы матрицы общего преобразования.

4. Осуществите поворот исходного треугольника вокруг точки с координатами (m,n) на угол q, используя при этом следующие последовательные преобразования:

a) переместите объект преобразования таким образом, чтобы точка, относительно которой совершается поворот, попала в начало координат;

b) выполните поворот объекта на требуемый угол вокруг точки начала координат;

c)осуществите обратное (по отношению к п/п. a) перемещение объекта.

5. Рассчитайте матрицу полного преобразования, реализованного в предыдущем пункте. Примените ее для преобразования исходного треугольника. Сравните результаты, полученные в настоящем и предыдущем пунктах.

Сформулируйте вывод о возможных путях реализации комбинаций двумерных преобразований.

6. Реализуйте симметричное отражение исходного треугольника относительно прямой линии 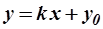, используя при этом следующие последовательные преобразования:

a) переместите объект преобразования вдоль оси x или y таким образом, чтобы прямая, относительно которой он отражается, прошла через точку начала координат;

b) поверните объект вокруг точки начала координат до совпадения прямой, относительно которой он отражается, с координатной осью xили y;

c) симметрично отразите объект относительно той оси, с которой в п/п. b совмещена прямая;

d) осуществите обратный (по отношению к п/п. b) поворот объекта;

e) осуществите обратное (по отношению к п/п. a) перемещение объекта.

7. Осуществите те же последовательные преобразования исходного треугольника, что и в пункте 6, но поменяв местами п/п.п. d и e. Сравните результаты полных преобразований, полученные в настоящем пункте и в пункте 6.

Сформулируйте вывод относительно коммутативности операции умножения матриц и, соответственно, о правилах реализации комбинаций преобразований.

8. Реализуйте по отношению к исходному треугольнику проецирование в однородных координатах.

Сделайте выводы о геометрическом смысле проведенного преобразования и процедуры нормализации результата умножения матриц. Сформулируйте также вывод относительно назначения коэффициентов правой верхней 2´1 подматрицы матрицы общего преобразования.

9. Осуществите общее масштабирование исходного треугольника.

Сформулируйте вывод относительно назначения коэффициента правой нижней 1´1 подматрицы матрицы общего преобразования.

10. Реализуйте преобразование исходного треугольника, используя матрицу общего преобразования со значениями коэффициентов p и q, приведенными в последнем пункте варианта задания.

Сформулируйте вывод относительно результата преобразования третьей вершины треугольника.

Таблица 1.

Дисциплина: «Компьютерная графика»
Лабораторная работа №2 Вариант задания №1
Координаты вершин исходного треугольника
x1 = 20; y1 = 10;x2 = 40; y2 = 70;x3 = 100; y3 = 50
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 2; d = 1,5 *
2d	c = 2 (или b = 1,5) *
2f	q = 50°
	m = 60; n = –80 *
	m = 10;n = 60;q = –75°
	k = 0,5; y0 = 60
	p = 0,005; q = 0,002 *
	s = 0,6 *
	p = – 0,02; q = 0,02 *
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)

Дисциплина: «Компьютерная графика»
Лабораторная работа №2 Вариант задания №2
Координаты вершин исходного треугольника
x1 = 10; y1 = 20;x2 = 60; y2 = 130;x3 = 170; y3 = 50
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 1,5;d = 2 *
2d	c = 0,5 (или b = 1,5)*
2f	q = 70°
	m = 75;n = –140 *
	m = 20;n = 140;q = –85°
	k = 0,185; y0 = 130
	p = 0,003; q = 0,002 *
	s = 0,7 *
	p = – 0,01; q = 0,014 *
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)
Дисциплина: «Компьютерная графика»
Лабораторная работа №2 Вариант задания №3
Координаты вершин исходного треугольника
x1 = 0; y1 = 0;x2 = –160; y2 = –170;x3 = –60; y3 = –170
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 2;d = 1,5 *
2d	c = –2 (или b = –3) *
2f	q = –41°
	m = 190; n = 50 *
	m = 40;n = 70;q = –65°
	k = 1,06; y0 = –140
	p = 0,006; q = –0,009 *
	s = –0,8 *
	p = –0,006; q = 0,008 *
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)

Дисциплина: «Компьютерная графика»
Лабораторная работа №2 Вариант задания №4
Координаты вершин исходного треугольника
x1 = –90; y1 = 10; x2 = 40; y2 = 170; x3 = 150; y3 = 50
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 1,7;d = 2 *
2d	c = –1,5 (или b = 0,8)*
2f	q = –67°
	m = –160;n = –200 *
	m = 40;n = 170;q = –72°
	k = 0,163; y0 = 175
	p = – 0,001; q = 0,003 *
	s = 0,65 *
	p = – 0,01; q = 0,01 *
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)
Дисциплина: «Компьютерная графика»
Лабораторная работа №2 Вариант задания №5
Координаты вершин исходного треугольника
x1 = –50; y1 = 60;x2 = –80; y2 = –100;x3 = 140; y3 = 120
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 2;d = 2*
2d	c = 1,4 (или b = 1,6)*
2f	q = 38°
	m = 90;n = –140 *
	m = 40;n = 120;q = –88°
	k = 1; y0 = –60
	p = –0,001; q = 0,002 *
	s = 2 *
	p = –0,02; q = 0,015 *
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)

Дисциплина: «Компьютерная графика»
Лабораторная работа №2 Вариант задания №6
Координаты вершин исходного треугольника
x1 = –165; y1 = –70;x2 = –70; y2 = –150;x3 = 160; y3 = –40
Пункт/подпункт программы работ	Параметры преобразования
2a	a = 1,5;d = 1,5 *
2d	c = –2 (или b = 0,5)*
2f	q = 55°
	m = 70;n = 150 *
	m = –50;n = –200;q = –53°
	k = 0,0925; y0 = –180
	p = –0,0001; q = 0,0009 *
	s = 0,6 *
	p = –0,005; q =0,005 *
* Значения остальных коэффициентов матрицы общего преобразования следует принимать такими же, как в матрице тождественного преобразования (см. приложение 1)