Вычисление конечных сумм и произведений

Теоретический материал

Решение многих задач связано с нахождением суммы или произведения элементов заданной последовательности. В данном разделе мы рассмотрим основные приемы вычисления конечных сумм и произведений.

Пусть 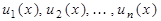- произвольная последовательность n функций. Будем рассматривать конечную сумму вида 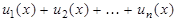. Такую сумму можно записать более компактно, используя следующее обозначение: 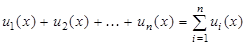. При 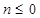значение суммы равно 0.

В дальнейшем будем также использовать сокращенную запись для конечного произведения данной последовательности, которая выглядит следующим образом: .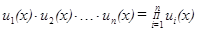

1. Написать программу, которая подсчитывает сумму натуральных чисел от 1 до n (n³1).

Указания по решению задачи. Пусть s_n - сумма натуральных чисел от 1 до n. Тогда s_n=1+2+…+(n-1)+n=(1+2+…+(n-1))+n=s_n-1+n, s₀=0. Мы пришли к рекуррентному соотношению s₀=0, s_n=s_n-1+n, которым мы можем воспользоваться для подсчета суммы. Соотношение s_n=s_n-1+n говорит о том, что сумма на n-ном шаге равна сумме, полученной на предыдущем шаге, плюс очередное слагаемое.

static void Main()

{

Console.Write("Ввведите значение n: ");

int n=int.Parse(Console.ReadLine());

int s=0;

for (int i=1; i<=n; ++i)

s+=i;

Console.WriteLine("s="+s);

}

2. Написать программу, которая подсчитывает n! для вещественного x и натурального n.

Указание по решению задачи. Из свойства факториала 0!=1!=1, n!=1*2*3*…*n, n!=(n-1)!n. Следовательно, факториал можно вычислять, используя рекуррентное соотношение b₀=1, b_n=b_n-1*n.

static void Main()

{

Console.Write("Ввведите значение n: ");

int n=int.Parse(Console.ReadLine());

int f=1;

for (int i=1; i<=n; ++i)

f*=i;

Console.WriteLine("{0}!={1}", n, f);

}

3. Написать программу для подсчета суммы 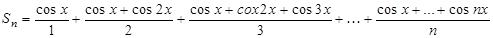, где х – вещественное число, n – натуральное число.

Указания по решению задачи. Если пронумеровать слагаемые, начиная с 1, то мы увидим, что номер слагаемого совпадает со значением знаменателя. Рассмотрим каждый числитель отдельно: 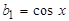, , 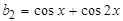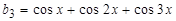… Эту последовательность можно представить рекуррентным соотношением b₀=0, b_n=b_n-1+cosnx (1). Теперь сумму можно представить следующим образом 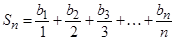, а для нее справедливо рекуррентное соотношение S₀=0, 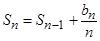(2). При составлении программы будем использовать формулы (1-2).

static void Main()

{

Console.Write("Ввведите значение n: ");

int n=int.Parse(Console.ReadLine());

Console.Write("Ввведите значение x: ");

double x=double.Parse(Console.ReadLine());

double b=0, s=0;

for (int i=1; i<=n; ++i)

{

b+=Math.Cos(i*x);

s+=b/i;

}

Console.WriteLine("s={0:f2}",s);

}

4. Написать программу для подсчета суммы 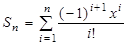, где х – вещественное число, n – натуральное число.

Указания по решению задачи. Перейдем от сокращенной формы записи к развернутой, получим 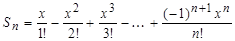. Каждое слагаемое формируется по формуле 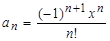. Если в эту формулу подставить n=0, то получим .

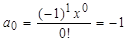Чтобы не вводить несколько рекуррентных соотношений (отдельно для числителя, отдельно для знаменателя), представим общий член последовательности слагаемых с помощью рекуррентного соотношением вида 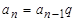, где q для нас пока не известно. Найти его можно из выражения 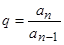. Произведя необходимые расчеты, получим, что 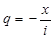. Следовательно, для последовательности слагаемых мы получили рекуррентное соотношение 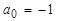, 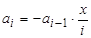(3). А всю сумму, по аналогии с предыдущими примерами, можно представить рекуррентным соотношением: S₀=0, 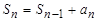(4). Таким образом, при составлении программы будем пользоваться формулами (3-4).

using System;

namespace Hello

{

class Program

{

static void Main()

{

Console.Write("Ввведите значение n: ");

int n=int.Parse(Console.ReadLine());

Console.Write("Ввведите значение x: ");

double x=double.Parse(Console.ReadLine());

double a=-1, s=0;

for (int i=1; i<=n; ++i)

{

a*=-x/i; s+=a;

}

Console.WriteLine("s={0:f2}",s);

}

}

}