Аппроксимация частотной характеристики
Поволжская государственная академия телекоммуникаций
И информатики
Кафедра "ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ"
Сдана на проверку Допустить к защите
"_____"___________ 2004 г. "_____"___________2004 г.
Защищена с оценкой _______
"_____"___________2004 г.
КУРСОВАЯ РАБОТА ПО ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
«РАСЧЕТ ФИЛЬТРОВ ПО РАБОЧИМ ПАРАМЕТРАМ»
Работу выполнила
студентка гр. МС-21
Исаева Д.Е.
Работу проверил
Дубинин А.Е.
2004 г.
Содержание:
1.Задание к курсовой работе 3
2. Постановка задачи синтеза электрического фильтра 3
3. Нормирование по частоте 4
Аппроксимация частотной характеристики рабочего ослабления фильтра 4
5. Реализация схемы ФНЧ 7
Денормирование по частоте 10
7. Расчет частотных характеристик фильтра 11
8. Проверка рабочего ослабления по элементам заданной схемы 13
9. Список использованной литературы 18
Задание к курсовой работе
Согласно варианту (166) требуется рассчитать фильтр нижних частот (ФНЧ), удовлетворяющий следующим техническим требованиям:
- граничные частоты полосы пропускания (ПП) f2 = 11,2 кГц;
- граничные частоты полосы непропускания (ПН) f3 = 22,4 кГц;
- макимально-допустимое значение рабочего ослабления в ПП ΔА =0,7 (дБ);
- минимально-допустимое значение рабочего ослабления в ПН Аmin =20 (дБ);
- сопротивление нагрузки R2 =550 (Ом).
Аппроксимацию требуется выполнить по Баттерворту, а реализацию – по Попову.
Постановка задачи синтеза электрического фильтра
Синтез электрического фильтра по рабочим параметрам (рабочему ослаблению или рабочей фазовой постоянной) состоит из двух этапов: аппроксимации и реализации.
На этапе аппроксимации необходимо получить аналитическое выражение рабочей передаточной функции Т(р) фильтра, удовлетворяющей условиям физической реализуемости по заданным требованиям.
На этапе реализации по найденной рабочей передаточной функции определяется схема фильтра и величины составляющих ее элементов.
В синтезе фильтров используется преобразование частоты и нормирование сопротивлений и частот.
Использование преобразования частоты позволяет свести расчет всех классов фильтров к расчету фильтра нижних частот (ФНЧ) и производить синтез любого фильтра в следующем порядке: сначала преобразовать заданную характеристику рабочего ослабления в низкочастотную, потом синтезировать ФНЧ, далее обратным частотным преобразованием перейти от элементов схемы ФНЧ к элементам (или комбинациям элементов) заданного фильтра.
Нормирование заключается в том, что вместо абсолютных значений частот и сопротивлений элементов цепи ФНЧ берутся их относительные величины. Нормирование осуществляется по отношению к нагрузочному сопротивлению и граничной частоте полосы пропускания для ФНЧ и ФВЧ (или среднегеометрической частоте полосы пропускания для ПФ).
Поэтому расчет любого фильтра начинается с расчета ФНЧ, нагруженного на нормированное сопротивление и с нормированной граничной частотой полосы пропускания, равной единице.
Техническими требованиями к фильтру являются:
- граничные частоты полосы пропускания (ПП) f2 или f2 , f21;
- граничные частоты полосы непропускания (ПН) f3 или f3 ,f31;
- максимально-допустимое значение рабочего ослабления в ПП ΔА (дБ) или коэффициент отражения ρ (%), которые связаны соотношением:
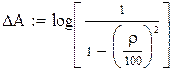 |
- минимально-допустимое значение рабочего ослабления в ПН Аmin(дБ);
- сопротивление нагрузки RН=R2 (Ом).
Синтез фильтра производится в следующем порядке:
1. Переход к ФНЧ-прототипу и нормирование частот;
2. Аппроксимация рабочей передаточной функции Т(р) и характеристики рабочего ослабления фильтра А(Ω);
3. Реализация схемы ФНЧ (ФНЧ-прототипа);
4. Переход от схемы ФНЧ к схеме заданного фильтра и денормирование ее элементов;
5. Расчет и построение денормированных частотных характеристик рабочего ослабления А(f) и рабочей фазы В(f) фильтра.
Нормирование по частоте
Нормирование производим относительно граничной частоты полосы пропускания f2:
Ω =- f / f2 ,
Тогда:
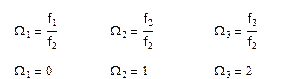
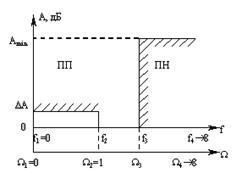
Рис.1 ФНЧ
Аппроксимация частотной характеристики
