Алгоритм критического пути

Широкое распространение получил простой и эффективный алгоритм списочного расписания: метод критического пути (method critical path).

Ш.1 Упорядочиваем в порядке убывания веса множество заданий; 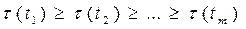, где ,

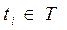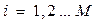
Ш.2 Начальная загрузка всех устройств равна нулю, выбирается первое устройство (процессор) 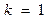и первое задание из множества заданий 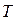, 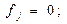для всех .

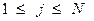Ш.3 Выбираем устройство, на котором будет обрабатываться текущее задание, (процессор) 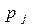с наименьшим 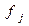среди всех процессоров (т.е. процессоров с минимальным временем загрузки на текущий момент).

Ш.4 Назначить 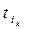следующим заданием на процессор 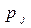. 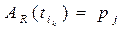, пересчитать .

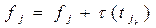Ш.5 Если 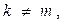то увеличить 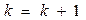и перейти на Ш.3 Иначе алгоритм заканчивается с построенным расписанием 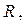общая длина которого равняется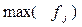

Решим задачу №1 алгоритмом Критический путь: выполнив Ш.1 множество заданий примет вид 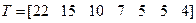. Согласно Ш.2 На первое устройство 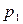назначается для выполнения задание 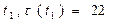. Расписание на 1-вом шаге:

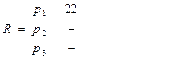
Считаем загрузку (время завершения выполнения работы) каждого процессора 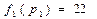, , 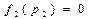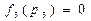. Выбираем следующий процессор с наименьшей загрузкой, т.е. 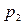, т.к. 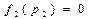. Назначаем следующую по порядку работу 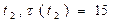Расписание на 2-ом шаге примет вид:

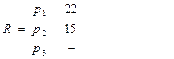
Пересчитав загрузку каждого процессора 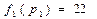, , 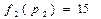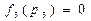переходим к Ш.4. Назначаем следующую работу 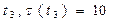на процессор с наименьшей загрузкой:

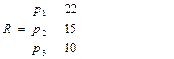
При 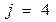назначаем следующую работу 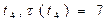на процессор 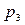(с наименьшей загрузкой), т.к :

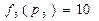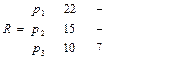
Текущая загрузка процессоров 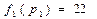> 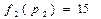< 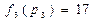значит, следующее задание 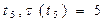назначается на процессор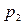

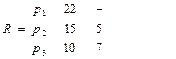
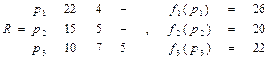
Выполнив все итерации, получаем расписание R

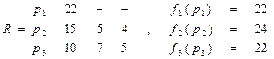
Критерий оценки алгоритма – максимальное время завершения выполнения работ: 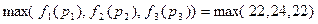=24

Упорядочивание в порядке возрастания

Алгоритм отличается от предыдущего лишь направлением сортировки множества заданий. Шаг 1 для данного алгоритма:

Ш.1 Упорядочиваем в порядке возрастания веса множество заданий; 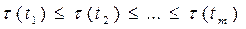, где 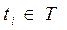, 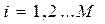при таком варианте в первую очередь выполняются задания с наименьшим весом. Последующие шаги соответствуют алгоритму, описанному в пункте 3.1.

Решим задачу №1 алгоритмом Упорядочивание в поярке возрастания: выполнив Ш.1 пункта 3.2 множество заданий примет вид 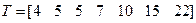. Итерационно выполнив шаги Ш.2-Ш.5, аналогично примеру, рассмотренному в пункте 3.1, получим расписание:

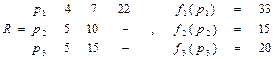
Результат: 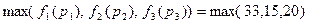=33

Случайный выбор

Множество заданий формируется случайным образом, и выполняется алгоритм пункта 3.1, начиная с шага 2.

Решим задачу №1 алгоритмом Случайный выбор: случайным образом получив множество заданий 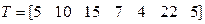. Итерационно выполнив шаги Ш.2-Ш.5, аналогично примеру, рассмотренному в пункте 3.1, получим расписание:

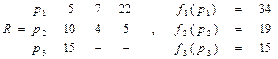
Результат: 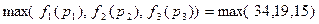=34

Алгоритм по направлению

Ш.1 Упорядочиваем в порядке убывания веса множество заданий; 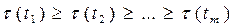, где ,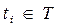

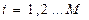
Ш.2 Начальная загрузка всех устройств равна нулю 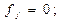для всех 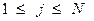, выбирается первое устройство (процессор) 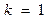и первое задание из множества заданий 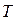назначается на процессор организуя проход справа налево.

Ш.3 Задания назначаются по порядку номеров 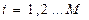на процессоры по их порядку номеров 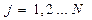для выполнения.

Ш.4 При достижении 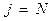порядок значений 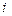остается прежним, а порядок изменения 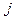меняется на обратный: организуется проход слева направо.

Ш.5 При изменении направления движения по 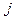проверяются условия: 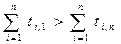, если проход осуществляется слева направо. Если же проход справа на лево, то 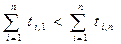. В случае невыполнения какого-то из условий для конкретного направления, то движение по 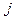не меняется до тех пор, пока не наступит выполнение соответствующего условия.

Ш.6 Если все задания назначены на выполнение, 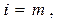то алгоритм заканчивается с построенным расписанием 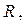общая длина которого равняется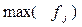

Решим задачу №1 алгоритмом по направлению: выполнив Ш.1 множество заданий примет вид .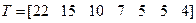

На первое устройство 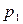назначается для выполнения задание 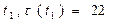. Расписание на 1-вом шаге:

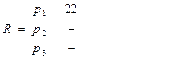
Назначаем следующее по порядку задание 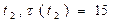. Расписание на 2-ом шаге примет вид:

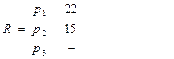
При 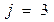назначаем задание 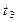на процессор :

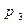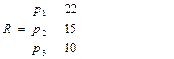
Считаем показатели загруженности процессоров “по краям”, т.е. суммарное время выполнения всех заданий на процессорах 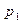и 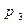, , 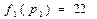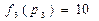. Т.к. 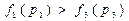, то при 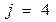назначаем следующую по порядку работу на процессор .

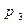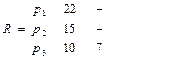
Пересчитываем суммарное время выполнения всех заданий на процессорах 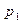и 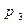, , 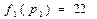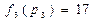. Т.к. 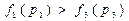, то при 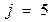назначаем следующую работу 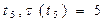на процессор .

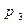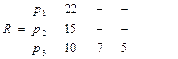
Пересчитываем показатели для процессоров 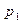и 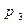, , 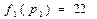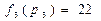. Т.к. условие 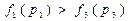не выполняется, то назначаем следующую работу 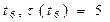на процессор 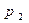, т.е. меняем “направление”.

Выполнив алгоритм до конца, получим расписание:

Критерий оценки алгоритма – максимальное время завершения выполнения работ: 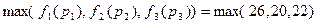=26

Генетический алгоритм

В задачах оптимизации часто применяется класс эвристических алгоритмов. К этому классу относятся и вероятностные эволюционные алгоритмы. Благодаря комбинированию случайного поиска и механизма уточнения(сохранения) решения даже при большом пространстве поиска решение может быть найдено в приемлемые временные рамки.

Рассмотрим общую схему работу Генетического алгоритма(ГА)

Ш.1 Формирование начального поколения

Ш.2 Отбор и применение ГА операторов для нового поколения

Ш.3 Проверка условия останова. Если не выполняется перейти к Ш.2

Ш.4 Лучшая особь выбирается как найденное решение.

В работе алгоритма используется набор решений, которые, как и в живой природе, борются с друг с другом за первенство. Лучшие выживают и передают свои свойства потомкам, худшие отмирают и не участвуют в отборе.

ГА является общим алгоритмом для решения любой задачи, и при его применении к конкретной необходимо выбрать механизм кодирования параметров задачи(фенотипа) в гены особи(генотипа), определить оптимизационную функцию 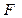(fitness function) и выбрать условия останова.

В данном случае решения задачи теории расписания минимаксный критерий будет являться оптимизационной функцией, а условием останова неизменность лучшего решения в течение 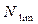поколений.

В качестве способа кодирования расписания в хромосому особи выберем следующий способ. В качестве гена 8ми битное целое число.

Вставить формулы преобразования

№раб
Вес
Ген
№приб

Оператор кроссовера. Основная задача сохранение решения благодаря обмену генетической информацией между особями.

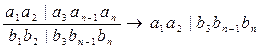
Особь A

№раб
Вес
Ген
№приб

Особь B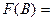

№раб
Вес
Ген
№приб

Особь С после кроссовера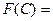

№раб
Вес
Ген
№приб

Оператор мутации. Осуществляет случайные изменения в хромосомах особей, тем самым исследуется пространство поиска.

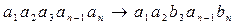
Особь А

№раб
Вес
Ген
№приб

Особь B после мутации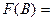

№раб
Вес
Ген
№приб

Для применения оператор кроссовера необходимо отобрать 2 особи из всего поколения, одним из простых способов является метод двоичного турнирного отбора. Для этого отбираются произвольно две особи из текущего решения 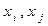и сравнивается их приспособленность 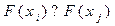лучшая особь участвует в кроссовере, вторую особь выбирают аналогично. При этом стоит не забывать, что все операторы также применяются с учетом вероятности, для кроссовера обычно задается уровень 0.95 (95% случаев он применяется), для мутации значительно меньший 0.05.

Еще одним механизмом сохранения решения является использование элитных особей. Данный метод заключается в том, что определенное фиксированное количество лучших особей переходит в каждое новое поколение без изменений.

Попробуем найти решение для параметров задачи указанных выше и следующими параметрами ГА

Вероятность кроссовера: 0.95

Вероятность мутации: 0.05

Кол-во особей: 10

Лимит останова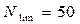

Использование Элиты: 1 особь

Ш.1 Начальное поколение

Поколение №0

Особи: SumF:378 0(S:48, ), 1(S:41, ), 2(S:32, ), 3(S:42, ), 4(S:37, ), 5(S:47, ), 6(S:26, ), 7(S:37, ), 8(S:37, ), 9(S:31, )

Лучшей особью является

Особь #6 Tmax: 26

[1 r:0] summ:26/26 4(4) 5(22)

[2 r:0] summ:22/22 2(15) 3(7)

[3 r:0] summ:20/20 0(5) 1(10) 6(5)

Поколение №1

Особи: SumF:361 1000(S:26, ), 1001(S:31, ), 1002(S:37, ), 1003(S:27, ), 1004(S:51, ), 1005(S:30, ), 1006(S:41, ), 1007(S:44, ), 1008(S:37, ), 1009(S:37, ),

Видно что в новом поколении лучшая особь не изменилась, но суммарная присобленность (SumF) улучшилась, что говорит о начале сходимости алгоритма вокруг лучшего решения.

…Пропускаем до 37 поколения

Поколение №37

Особи: SumF:264 1000(S:26, ), 1001(S:26, ), 1002(S:26, ), 1003(S:26, ), 1004(S:24, ), 1005(S:26, ), 1006(S:26, ), 1007(S:26, ), 1008(S:26, ), 1009(S:32, )

Лучшей особью является

Особь #1004 Tmax: 24

[1 r:1] summ:22/22 5(22)

[2 r:2] summ:24/24 2(15) 4(4) 6(5)

[3 r:3] summ:22/22 0(5) 1(10) 3(7)

Поколение №38

Особи: SumF: 267 0(S:24, ), 1(S:26, ), 2(S:30, ), 3(S:26, ), 4(S:26, ), 5(S:26, ), 6(S:31, ), 7(S:26, ), 8(S:26, ), 9(S:26, )

…Пропускаем до 87 поколения. Останов алгоритма.

Особи: SumF: 263 1000(S:24, ), 1001(S:24, ), 1002(S:27, ), 1003(S:24, ), 1004(S:24, ), 1005(S:24, ), 1006(S:44, ), 1007(S:24, ), 1008(S:24, ), 1009(S:24, )

Любая из особей с Tnax:24 может быть выбрана как решение.

Особь #1004 Tmax: 24

[1 r:1] summ:22/22 5(22)

[2 r:2] summ:24/24 2(15) 4(4) 6(5)

[3 r:3] summ:22/22 0(5) 1(10) 3(7)

Графически процесс решения можно увидеть на след графике.

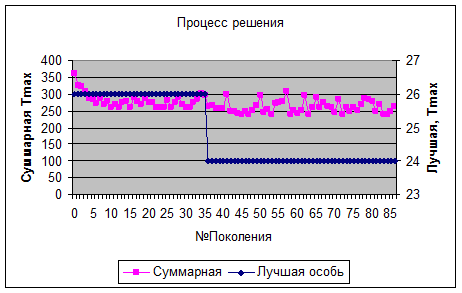Варианты заданий

Задание определяется согласно № - номера студента в списке, по приведенным ниже таблицам (Таблица 1, Таблица 2, Таблица 3). Алг. - название алгоритма, который необходимо запрограммировать. Параметр n-определяет число устройств. m– количество работ, выбирается одно значение из указанного отрезка в таблице 3, T – множество весов работ, случайным образом берется m работ в пределах указанных в таблице 3.

Например, если студент в списке под номером №5, то Алг. = “Критический путь”, n = 4, m выбирается произвольно в отрезке [20,25] m = 21, T формируется из n работ, вес которых выбирается случайным образом в отрезке [20,35].

Таблица 1

№

Алг.

Критический путь

Случайный выбор

n

m, T

Таблица 2

№

Алг.

В порядке возрастания

Алг. по направлению

n

m, T

Таблица 3

m, T		20-25	20-35
	30-35	35-40

Литература

1. Коффман Э.Г. “Теория расписания и вычислительные машины” – M.: “Наука”, 1987

1. Романовский И.В. “Алгоритмы решения экстремальных задач” – М.: “Наука”, 1977

1. Пашкеев С.Д., Минязов Р.И., Могилевский В.Д. “Машинные методы оптимизации в технике связи” – М.: “Связь”, 1976.