Некоторые алгоритмы обработки одномерных массивов

Рассмотрим несколько часто встречающихся на практике задач обработки одномерных массивов.

Пример 1. Поиск наибольшего элемента в одномерном массиве.

Исходными данными в поставленной задаче являются массив x и его размерность n. Решение этой задачи осуществляется с помощью цикла по параметру i, изменяющегося с шагом +1 от 1 до n-1. Перед входом в цикл переменной max присваивается значение первого элемента массива х[0].

С каждым итерацией цикла происходит переход к новому элементу массива и сравнение его значения со значением, хранящемся в переменной max. Если значение текущего элемента массива оказывается больше значения max, то переменной max присваивается значение элемента массива с текущим порядковым номером. После выхода из цикла выводится найденное значение наибольшего элемента массива.

Схема алгоритма приведена на рис. 1, программа в лист. 1.

Рисунок 1 – Схема алгоритма к примеру 1

Листинг 1 – Поиск максимального элемента в одномерном массиве

using System;

namespace ConsoleApplication5

{

class Program

{

static void Main(string[] args)

{

const int n = 6;

int[] a = new int[n] { 3, 12, 5, -9, 8, -4 };

Console.WriteLine("Исходный массив:");

for (int i = 0; i < n; ++i)

Console.WriteLine("\t" + a[i]);

Console.WriteLine();

int max = a[0];

for (int i = 0; i < n; ++i)

if (a[i] > max)

max = a[i];

Console.WriteLine("Максимальный элемент = " + max);

Console.Read();

}

}

}

Обратите внимание на то, что для вывода элементов исходного массива требуется организовать цикл.

Результаты работы программы:

Пример 2.Сортировка элементов одномерного массива по убыванию методом выбора.

Введем дополнительные определения:

x – исходный массив, который нужно упорядочить;

max – максимальный элемент массива;

im – индекс максимального элемента;

сh – переменная для обмена элементов;

exch – признак нахождения max в неотсортированной части массива.

Суть представленного на рис.4 алгоритма заключается в следующем. Упорядочение начинается с поиска элемента, который должен находиться на первом месте в отсортированном массиве. Таким элементом является максимальный элемент всего массива.

После нахождения такого элемента происходит его установка на первое место в массиве, а первый элемент устанавливается на место найденного наибольшего элемента. Далее считая, что первое место в массиве занято необходимым элементом, оно исключается из рассмотрения, и описанные выше действия применяются к его оставшейся части: поиск наибольшего элемента в неупорядоченной части и его обмен с первым элементом этой части.

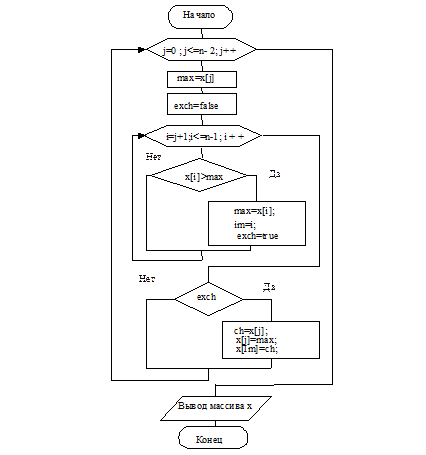
Рисунок 2 – Схема алгоритма к примеру 2

Программа для данного алгоритма, приведена в лист. 2.

Листинг 2– Сортировка одномерного массива методом «выбора»

using System;

namespace ConsoleApplication7

{

class Program

{

static void Main(string[] args)

{

const int n = 6;

int ch;

int[] x = new int[n] { 3, 12, 5, -9, 8, -4 };

Console.WriteLine("Исходный массив:");

for (int i = 0; i <= n - 1; ++i)

Console.Write(" " + x[i]);

int im = n - 1;

for (int j = 0; j <= n - 2; j++)

{

int max = x[j];

bool exch = false;

for (int i = j + 1; i <= n - 1; ++i)

if (x[i] > max)

{

max = x[i];

im = i;

exch = true;

}

if (exch == true)

{

ch = x[j];

x[j] = max;

x[im] = ch;

}

}

Console.WriteLine();

Console.WriteLine("Результирующий массив:");

for (int i = 0; i <= n - 1; ++i)

Console.Write(" " + x[i]);

Console.Read();

}

}

}

Результат работы программы:

Пример 3.Сортировка элементов одномерного массива по убыванию методом вставки.

Обозначения:

x– исходный массив, который нужно упорядочить;

n– количество элементов массива;

i,j,k – переменные цикла;

ch– переменная обмена.

Схема алгоритма представлена на рис. 3, программа в лист. 3. Суть метода состоит в следующем. Предполагается, что первый элемент массива уже стоит на своём месте. Чтобы упорядочить второй элемент массива, нужно найти для него такое место в упорядоченной части массива, чтобы упорядоченность сохранялась. Затем требуется вставить этот элемент на найденное место. Чтобы упорядочить все элементы массива, эти действия нужно выполнить n-1 раз, т.е. для всех элементов, кроме первого.

Схема алгоритма решения данной задачи по структуре представляет собой внешний цикл для выполнения указанных выше действий, который содержит еще два вложенных в него следующих друг за другом цикла.

Первый из них организован как цикл с предусловием для поиска в упорядоченной части массива такого элемента массива, чье значение будет больше величины устанавливаемого элемента. Для достижения этой цели в указанном цикле осуществляется продвижение от конца упорядоченной части к ее началу путем уменьшения номера элемента i с каждой итерацией на единицу. Выход из цикла осуществляется тогда, когда такой элемент будет найден, либо будет достигнуто начало упорядоченной части.

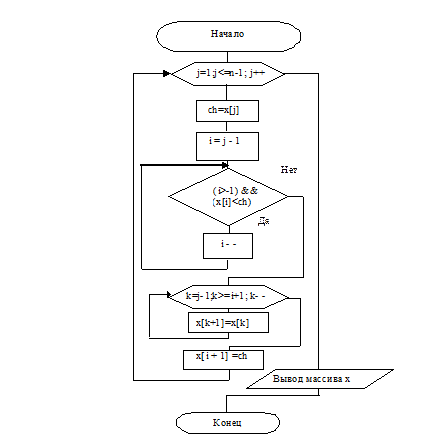
Рисунок 3 – Схема алгоритма к примеру 3

Следующий за ним цикл производит перемещение элементов упорядоченной части, начиная с ее конца и заканчивая i+1 элементом, на один элемент вправо для освобождения места упорядочиваемому j элементу.

После выхода из цикла (цикл с параметром) производится запись j элемента, хранимого в переменной ch, на освобожденное место.

Листинг 3 – Сортировка одномерного массива методом «вставки»

using System;

namespace ConsoleApplication7

{

class Program

{

static void Main(string[] args)

{

const int n = 6;

int ch;

int[] x = new int[n] { 3, 12, 5, -9, 8, -4 };

Console.WriteLine("Исходный массив:");

for (int i = 0; i <= n - 1; ++i)

Console.Write(" " + x[i]);

for (int j = 1; j <= n - 1; j++)

{

ch = x[j];

int i = j - 1;

while ((i > -1) && (x[i] < ch))

i--;

for (int k = j - 1; k >= i+1; --k)

x[k + 1] = x[k];

x[i+1] = ch;

}

Console.WriteLine();

Console.WriteLine("Результирующий массив:");

for (int i = 0; i <= n - 1; ++i)

Console.Write(" " + x[i]);

Console.Read();

}

}

}

Результат работы программы:

Пример 4.Сортировка элементов одномерного массива по возрастанию методом «пузырька».

Обозначения:

x– исходный массив, который нужно упорядочить;

n – количество элементов массива;

i,j– переменные цикла;

ch– переменная обмена;

exch– признак существования инверсии.

Листинг4 – Сортировка одномерного массива методом «пузырька»

using System;

namespace ConsoleApplication7

{

class Program

{

static void Main(string[] args)

{

const int n = 6;

int ch;

int[] x = new int[n] { 3, 12, 5, -9, 8, -4 };

Console.WriteLine("Исходный массив:");

for (int i = 0; i <= n - 1; ++i)

Console.Write(" " + x[i]);

for (int j = 0; j <= n - 1; j++)

{

bool exch = false;

for (int i = 0; i <= n - 2 - j; ++i)

if (x[i] > x[i + 1])

{

ch = x[i + 1];

x[i + 1] = x[i];

x[i] = ch;

exch = true;

}

if (exch == false) break;

}

Console.WriteLine();

Console.WriteLine("Результирующий массив:");

for (int i = 0; i <= n - 1; ++i)

Console.Write(" " + x[i]);

Console.Read();

}

}

}

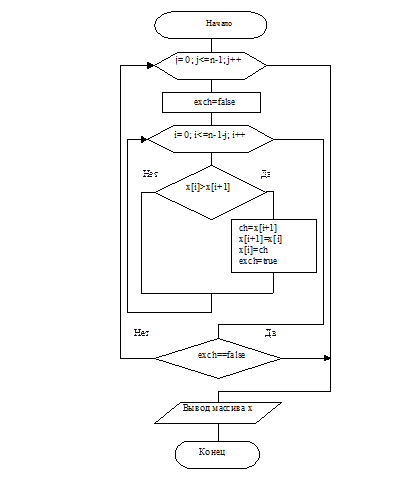
Рисунок 6 – Схема алгоритма к примеру 4

Суть метода состоит в последовательном просмотре соседних элементов массива. Если они нарушают требуемый порядок следования, то они меняются местами – осуществляется инверсия. Просмотр нужно выполнить n-1 раз.

Очень существенна проверка на наличие инверсии (нарушения порядка). Если в процессе просмотра массива была осуществлена хотя бы одна инверсия (exch=true), то просмотр массива повторяется. В противном случае (exch=false) в массиве уже все элементы упорядочены и целесообразно прервать работу цикла оператором break. Схема алгоритма представлена на рис. 4, программа в лист. 4.

Результат работы программы:

Класс System.Arrау

Для облегчения программирования задач обработки массивов данных в С# все массивы имеют общий базовый класс Аrrау, определенный в пространстве имен System. Несколько полезных методов этого класса приведены в табл. 1.

Таблица 1- Основные элементы класса Аrrау

Элемент	Вид	Описание
Length	Свойство	Количество элементов массива (по всем размерностям)
Rank	Свойство	Количество размерностей массива
BinarySearch	Статический метод	Двоичный поиск в отсортированном массиве
Сlear	Статический метод	Присваивание элементам массива значений по умолчанию
Сору	Статический метод	Копирование заданного диапазона элементов одного массива в другой массив
СоруТо	Метод	Копирование всех элементов текущего одномерного массива в другой одномерный массив
GetValue	Метод	Получение значения элемента массива
IndexOf	Статический метод	Поиск первого вхождения элемента в одномерный массив
LastIndexOf	Статический метод	Поиск последнего вхождения элемента в одномерный массив
Reverse	Статический метод	Изменение порядка следования элементов на обратный
SetValue	Метод	Установка значения элемента массива
Sort	Статический метод	Упорядочивание элементов одномерного массива

Свойство Length позволяет реализовывать алгоритмы, которые будут работать с массивами различной длины. Использование этого свойства вместо явного задания размерности исключает возможность выхода индекса за границы массива. В листинге продемонстрировано применение двух элементов класса Аrrау при работе с одномерным массивом.

Листинг 5 – Использование методов класса Аrrау

using System;

namespace ConsoleApplication1

{

class Class1

{

static void Main()

{

int[] x = { 21, 2, 14, -6, 38, -7, 30};

Console.WriteLine();

Console.WriteLine("Исходный массив:");

for (int i = 0; i < x.Length; ++i)

Console.Write(" " + x[i]);

Array.Sort(x);

Console.WriteLine();

Console.WriteLine("Упорядоченный массив:");

for (int i = 0; i < x.Length; ++i)

Console.Write(" " + x[i]);

Array.Reverse(x);

Console.WriteLine();

Console.WriteLine("Обратный порядок в массиве:");

for (int i = 0; i < x.Length; ++i)

Console.Write(" " + x[i]);

Console.Read();

}

}

}

Методы Sort, Reverse являются статическими, поэтому к ним обращаются через имя класса Array, а не экземпляра, и передают в них имя массива.

Как видно по результатам работы программы метод Sort осуществляет сортировку массива по возрастанию. Применив к массиву, отсортированному таким образом, метод Reverse, получим массив, отсортированный по убыванию.

Результаты работы программы: