Системы счисления. Правила перевода

Перевод чисел из одной системы в другую.

1. В десятичную систему счисления:

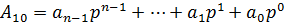
2. В двоичную и остальные системы счисления.

Перевод целой части:

1. Разделить А/2. Получим q + остаток α

2. Если 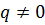, то принять его за новое делимое и обвести α

3. Вернуться к шагу 1

4. Если q=0, то алгоритм прекращается, выписать остатки в порядке обратном их получения.

3. Перевод из двоичной системы: 0001 0101 1011 = 337

4. Перевод дробных чисел:

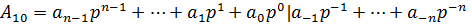
Алгоритм перевода десятичной дроби в другую систему счисления:

1. Выделить целую часть и выполнить ее перевод по требуемой системе счисления по известному алгоритму

2. Выделить дробную часть и умножить ее на основание выбранной новой системы счисления

3. Полученные после умножения дробной части числа, выделить целую часть и принять ее в качестве значения первого после запятой разряда в новой системе счисления

4. Если дробная часть получается после умножения равной нулю, процесс перевода прекращается.

Процесс также можно прекратить, если достигнута необходимая точность вычисления.

5. Перевод чисел со знаком.

Отличительным признаком числа со знаком является особая приставка старшего бита представляющего числа.

Для отрицательных чисел:

Старший бит 0 – число положительное

Старший бит 1 – число отрицательное, а это предполагает, что оно записано в дополнительном коде.

Пример:

А= -185 = 11111111|01000111; |185| = 10111001

Алгоритм:

1. Выделяется модуль числа

2. Инвертируется каждый бит двоичного числа и прибавляется 1

Обратный перевод из дополнительного кода в основной:

1. Выполнить инвертирование битов двоичного дополнения

2. К полученному двоичному числу прибавить 1.