Внутренняя сортировка (массивов).

Задачу внутренней сортировки можно формально представить следующим образом: Для

заданной последовательности ключей a1 ,a2 ,...,an необходимо найти перестановку

a(j1) ,a(j2) ,...,a(jn) для которой выполняется условие g^-1( a(j1))=< g^-1(a(j2) ) =<... g^-1( a(jn))

Другими словами мы предполагаем, что на множестве ключей элементов исходной

последовательности определено отношение линейного порядка, и задача заключается в

построении последовательности, для которых этот порядок выполняется. При внутренней

сортировке обычно стараются не использовать дополнительную память.

Нижние оценки.При построении эффективных алгоритмов необходимо понимать, к

какой временной оценке его работы мы должны стремиться. Построение нижних оценок

временной сложности является достаточно серьезной задачей и значения оценки может

зависеть как от объема исходной информации, так и ограничений, налагаемых на

вычислитель. Часто нижние оценки получаются из мощностных соображений

(энтропийный подход), иногда при построении удается использовать структурные

особенности задачи. В большинстве своем энтропийный подход дает неэффективные

нижние оценки (устанавливается лишь факт существования объекта определенной

сложности без конструктивного описания самого объекта)³⁷. В этом случае бывает обычно

трудно построить как объекты, которые имеют соответствующую сложность, так и

алгоритмы описания таких объектов. Однако введение разумных ограничений и

выделение соответствующих классов задач нередко позволяют находить нижние

сложностные оценки с точностью до порядка роста соответствующих функций,

участвующих в оценке.

Рассмотрим задачу построения нижних временных оценок для сортировки данных при

ограничении, что у нас нет подробной информации о структуре объектов исходной

последовательности, но имеется возможность сравнения любых двух объектов этой

последовательности.

Очевидно, тривиальной нижней оценкой для задачи сортировки размерности n является

линейная функция O(n), поскольку каждый элемент исходной последовательности

должен обрабатываться соответствующим алгоритмом. С другой стороны задачу

сортировки можно рассматривать как задачу поиска подходящей последовательности во

множестве всех перестановок. Известно, что всего имеется n! перестановок из n

элементов. Присвоим каждой перестановке номер в виде двоичного вектора некоторой

длины так, чтобы разным перестановкам соответствовали разные вектора. Поскольку

число двоичных векторов длины m равно 2^m , то должно выполняться условие 2^m >= n!, из

которой следует мощностная оценка m >= log n!, которая утверждает, что самое длинное

описание перестановки в качестве двоичной последовательности будет O(nlog n) .

Возникает вопрос, как связаны двоичные вектора с последовательностью шагов алгоритма

сортировки? Рассмотрим класс алгоритмов, которые в качестве базовых операций используют операции сравнения элементов и операции их перестановки. Тогда операция

сравнения двух любых элементов a(i) и a(j) разбивает множество всех перестановок на два

подмножества A(ai<aj) и A(ai>aj). Каждое из полученных подмножеств³⁸ также можно разбить

на части, используя другое сравнение. Аккуратная реализация этой идеи приводит к

построению дерева решений, листьями которого являются различные порядки³⁹

следования элементов исходного множества, а внутренние вершины представляют

результат решения, которое принимается после сравнения соответствующих элементов

множества. Ниже приведен пример дерева решений для множества {a,b,c}. В листьях

дерева указан порядок сортировки в зависимости от принятых решений

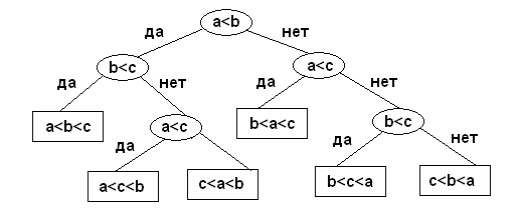
В [2] доказано, что высота любого дерева решений, упорядочивающего

последовательность из n различных элементов не меньше log(n!). Из этого результата

вытекает важное следствие:

В любом алгоритме, упорядочивающем с помощью сравнений, на упорядочивание

последовательности из n элементов, тратится не менее O(nlog n) шагов при некоторой

константе c и достаточно большом n .

Эта оценка справедлива в случае, когда при сортировке не используется дополнительная

информация, которая может содержаться в элементах исходного множества. Наличие

подобной информации в ряде случаев позволяет проводить сортировку без сравнений

элементов друг с другом и понизить нижнюю оценку до O(n).

Верхние оценки. Пожалуй, никакая другая проблема не породила такого количества

разнообразнейших алгоритмов, как задача сортировки. Существует ли некий

"универсальный", наилучший алгоритм? В определенном смысле, нет. Однако, имея

приблизительные характеристики входных данных, можно подобрать метод, работающий

оптимальным образом. Алгоритмы сортировки разбиваются на два класса:

1. Алгоритмы, которые используют только операции сравнения ключей и

перестановки элементов;

2. Алгоритмы, которые используют внутреннюю структуру элементов исходного

множества.

Сначала исследуем алгоритмы первого класса. Временная сложность алгоритма

складывается из числа сравнений и числа перестановок элементов исходного множества.

Число сравнений в алгоритмах сортировки принято обозначать через C , соответственно

для числа обменов будем использовать символ M ⁴⁰. При исследовании сложности

обычно выделяют три случая: минимальную сложность алгоритма (Cmin + Mmin - обычно

она достигается для уже отсортированной последовательности и в этом случае

подсчитывается число шагов, необходимых для подтверждения факта отсортированности

исходной последовательности), для худшего случая ( Cmax + Mmax - обычно, худший случай

достигается на последовательности, отсортированной в обратном порядке) и среднее

значение сложности ( Cave + Mave ), взятое по всем возможным последовательностям на

входе алгоритма при условии, что каждое из них встречается с одинаковой вероятностью.

Множество алгоритмов внутренней сортировки, в зависимости от используемых методов,

обычно делится на несколько классов:

1. Сортировка включениями

2. Сортировка выбором

3. Сортировка обменом

4. Сортировка слияние

Различие между этими методами достаточно условное. Поскольку на каждом шаге

алгоритм работает только с парой элементов, то каждый алгоритм в процессе своей

работы должен формировать линейно упорядоченные подмножества, объединение

которых на завершающей стадии работы алгоритма и дают необходимый результат.

Первоначально исходная последовательность состоит из одиночных несвязанных между

собой элементов. Каждое сравнение некоторых выбранных элементов с последующей

возможной их перестановкой определяет подмножества из двух элементов, которые

находятся в необходимом отношении. Рассматривая полученное подмножество как

самостоятельный объект, и вводя специальные операции на таких объектах можно

строить все более длинные последовательности. Большинство алгоритмов сортировки на

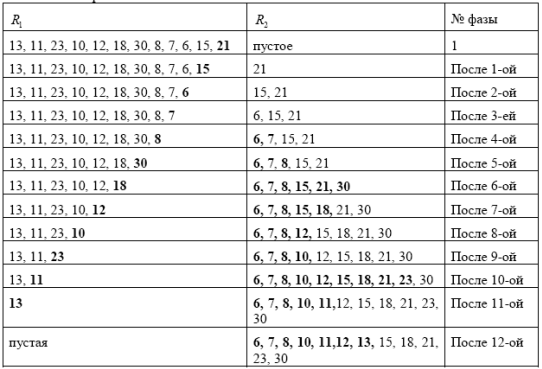
каждом шаге разбивают текущую последовательность на две части: множество R1

элементов, из которого извлекается информация об элементе или группе элементов, и

множество R2 элементов, которое по шагам формируется алгоритмом. Разбиение

последовательности на части R1 и R2 может меняться в зависимости от этапа построения

(иногда, значительно), и поэтому хорошие алгоритмы должны формулировать простые

правила построения этого разбиения. Очень часто разбиение строится на единой

структуре данных путем указания границ соответствующих частей с использованием

указателей (плавающих границ). Алгоритм использует R1 как источник данных, основной

операцией на R1 является задача поиска элемента (группы элементов), удовлетворяющего

некоторому условию. R2 является приёмником, который должен уметь дополнять себя

элементами из R1 с сохранением требуемого порядка элементов (для этого необходимо

уметь решать задачу объединения множеств с сохранением имеющегося на них порядка).

В процессе работы алгоритма R1 и R2 могут меняться местами, накапливая информацию

о последовательности в целом. Поэтому с множеством R1 можно связать операции поиска

элемента (обычно минимального или максимального), удаления элемента и поверки

пустоты множества. С R2 связывается операции вставки. Но поскольку R1 и R2

реализуются как части одной структуры, то вообще говоря, в задаче сортировки мы имеем

один абстрактный тип данных множество с операциями поиска, вставки, удаления и

проверки пустоты.

Не претендуя на полный обзор алгоритмов сортировки (достаточно подробное и полное

их описание приведено в [14]), проанализируем некоторые из них. Без ограничения

общности можно ограничиться рассмотрением сортировки по неубыванию (случай

невозрастания является симметричным и имеет те же оценки сложности).

Сначала рассмотрим алгоритмы, в которых на каждом шаге формирования

последовательности R2 участвует ровно один элемент.

Простое включение.Пусть исходная последовательность A имеет вид a1,a2,..,an.

Положим R1 = {a1, a2, a3… an} и R2=пустое множество . Идея алгоритма заключается в выборе

произвольного элемента a(t) из R1 и слияния упорядоченной последовательности R2 с

одноэлементной последовательностью a(t) с сохранением отношением порядка на R2 .

Поскольку порядок выбора элемента из R1 произволен, то элементы могут выбираться в

том порядке, в каком они расположены в исходной последовательности. Другими

словами, в этом случае задача поиска в R1 - тривиальна и выбор элемента занимает

константное время.