Системы умножения и их структурные проекции

Как и я сказал, мы будем охватывать всё. Поэтому раз структурные проекции – мы будем разбирать относительно каждой пространственной структуры, как она проецируется куда-то.

Ну давайте её отложим. Азъ и поставим.

│а│

Т.е. она у нас будет обозначать любую структуру и отображать любую проекцию. А теперь представьте: есть миры и пространства, есть миры с дробными пространствами, есть внепространственное что-то. И вот представьте, и это что-то внепространственное, оно же все равно имеет какую-то характеристику. Правильно? А как мы единое передадим вне всякого пространства? А это и будет та самая изначальная точка. Понятно, да? Хорошо, чтобы было понятней, я вам процитирую Книгу Света, харатья 1: "Некогда, вернее тогда, кода не было пространства и времен нами людьми воспринимаемых, был не воплощаясь Един Великий Рамха. Он проявился в новую действительность и от восприятия новой бескрайней бесконечности озарился великим светом радости". Т.е. видите, Веды говорят что было такое состояние, когда не было времен и пространства. Значит что-то было безвременное и безпространственное. Но заметьте, он проявился в новую действительность. А это о чем говорит? Что где-то была старая действительность, где он, возможно, был не один. Ну, наткнулся он на новую действительность и от него пошел Свет, и появились новые Вселенные. Т.е. это та самая точка. Которую ученные называют точкой сингулярности,т.е. когда, вся вселенная или что бы то ни было, была когда-то в единой, непространственной структуре. Только они до сих пор и не знают, кто поднес спичку, у них же до сих пор идея вселенского взрыва. А это просто не воплощаясь Рамха проявился и вот свет радости, поток Инглии, он наполнил жизнью и жизнь появилась. Вот она единая точка. Т.е. как бы в нулевом, беспространственном, я его поставил как бы сферическое проявление. Азъ, он был един не воплощаясь.

│а│º = 1

Т.е. как бы Азъ внулевом это есть единый, изначальный.

Ну потом, свет пошел, начал соединять. Азъ появилась первая пространственная характеристика, которую начал наполнять свет.

│а│¹

И заметьте, и как только свет, Инглия, истек, он начал наполнять, и в этот момент, как говорят Веды, в новой действительности появилось Велике Сверхгигантское Нечто. А так как оно не было тем, чем являлся Великий Рамха, значит она стала точкой противоположности. А если есть что-то одно и ему противоположное, это чему равно? Двум. Как бы светлое и темное.

│а│¹ = 2

А теперь, мы запишем подправило: "Любая фигура, объект или структура одномерного пространства будет иметь две опорные точки".

И когда вы в школе изображали оси координат, вы что рисовали?- где-то минус бесконечность, где-то плюс бесконечность. И вот это плюс бесконечность – это положительное светлое, а минус как бы мрачное, уходящее во мрак. Все текло от плюса к минусу. И так же и в этой (прим. вертикальной) пространственной оси.

Далее. Вот мы перешли к двухмерному пространству. Вот сейчас мы перейдем к проекции. Т.е. мы имеем, что на сей момент – какой-то отрезок одномерного пространства. Чтобы получить его структурную характеристику в двухмерном пространстве, мы должны провести проекцию к длине отрезка и на длину данного отрезка.

И это я запишу следующим образом: "а" первого пространства, первой мерности спроецирован на "а" первой мерности. Сколько здесь у меня?- две мерности. И что у меня получилось?- четыре (рис.1)

(рис.1)│а│² = │а│¹ ┴ │а│¹ = 4

Т.е. мы получили проекцию квадрата, у которого 4 опорные точки.

Чтобы получить фигуру трехмерного пространства мы должны "а" второе спроецировать на "а" второе. Объясняю, что мы делаем. Мы должны провести проекцию уже не к линии, к отрезку, мы должны провести проекцию квадрата на длину квадрата. И мы получили уже куб. и сколько опорных точек?- 8

│а│³ = │а│² ┴ │а│² = 8

А теперь посмотрите на свои формулы – определенная прогрессия. Т.е. чтобы получить четырехмерную фигуру мы должны что сделать?- мы должны провести проекцию третьей на длину третьей. Т.е. мы должны что?- спроецировать куб на длину куба (рис. 2)

(рис. 2)

Таким образом, мы его проецируем разворачивая. И получилось 16 опорных точек.

│а│⁴ = │а│³ ┴ │а│³ = 16

Дальше идет принцип, который никто не отвергал. Многие говорят: "А чем вы докажете". - С компьютерами дело все имеют? Память. Сначала 4 Мб, потом появилось 8, потом 16. значит в пятимерном пространстве эта фигура будет иметь 32 опорные точки. В шестимерном пространстве – 64, в семимерном - 128, в восьмимерном – 256. (рис. 3)

| a |⁵ ≡| a |⁴ | a |⁴ ≡32

| a |⁶ ≡| a |⁵ | a |⁵ ≡64

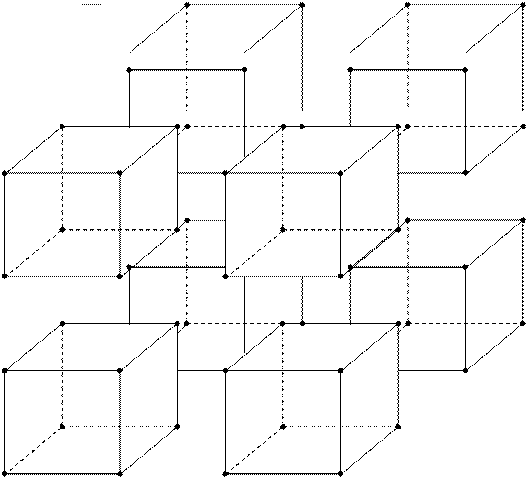
(рис. 3)

Шестнадцатимерное пространство, оно есть следующее гармоничное пространство за нашим. Если у нас здесь открыты 16 каналов для того чтобы мы познали 16-мерное пространство, там-то у нас будет раскрыто 256. Это мы познаем. А структурная разверстка идет с увеличением, значит что?- 65 536 опорных точек. Всего!

И заметьте, куб сколько имеет?- 8 опорных точек. Когда говорим ЖДЫ, умножение, мы говорим о трехмерности – дважды. А когда я говорю "два", значит два куба в пространстве.

Дважды два – шестнадцать. Дошло?

Потому что когда в школе вам сказали: два плюс два – четыре, дважды два – четыре, два во второй степени – четыре, вас два раза из трех обманули. Два плюс два – четыре, дважды два – 16, а два во второй степени будет 3,99999999… - оно никогда не будет равно 4, потому что мерность нашего пространства не равно трем.

Пишем дальше тему.

Определение мерности при использовании четко структурных изображений

│а│² = 3

(а = 3)

Раз оно трехмерное, то я и изображаю вам данную четкую структуру. (рис. 4)

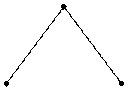(рис. 4)

Т.е. здесь мы также занимаемся проекцией, только не в гармоничной форме, а в отображении к четкой структуре. Поэтому (рис. 5)

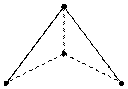
(рис. 5) | а |³ = 4

Чтобы получить 4-мерную фигуру я должен что сделать?- спроецировать структурно данную фигуру. (рис. 6)

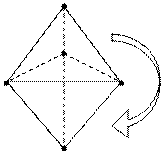(рис. 6) | а |⁴ = 5

И у меня получилось что?- два тетропака соединены между собой.

А теперь | а |⁵:(рис. 7)

5’

3’

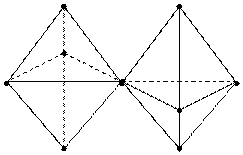
| а |⁵ = 9 (точка №1 является общей для обоих проекций)

(рис. 7)

Дальше, 6-тимерная: (рис. 8)

| а |⁶ ≡| а |⁵ | а |⁵ - 2 (общие точки) ≡16

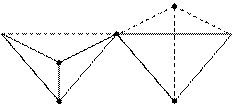(рис. 8)

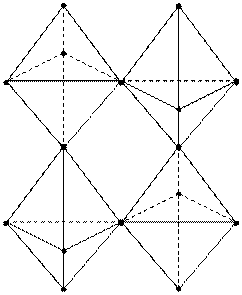
А теперь представьте семимерная: (рис. 9)

| а |⁷ ≡ | а |⁶ | а |⁶ ≡16 + 16 – 4 (общ.точки) ≡28

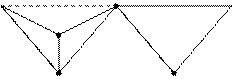(рис. 9)

И вот на этой системе и построено умножение.