Представление чисел в двоичном коде

Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах – минимальных по размеру адресуемых ячейках памяти. Вся память компьютера разбита на отдельные участки из 8 бит (т.е. на байты). Байты имеют номера: 0, 1, 2, …, называемые адресами. Два соседних участка: 0 и 1, 2 и 3 и т.д. образуют ячейку памяти ЭВМ. Т.е. одна ячейка памяти может хранить два байта или 16 битов информации. Для содержимого одной ячейки используют название – «машинное слово» или просто «слово». Очевидно, адресом числа считается адрес первого байта, т.е. четные числа, начиная с 0, 2, 4, 6 и т.д. В байте может содержаться произвольный код из восьми двоичных разрядов, и задача представления состоит в том, чтобы указать правила, как в одном или нескольких байтах записать число.

Числа могут быть целые точные, дробные точные, рациональные, иррациональные, дробные приближенные, положительные и отрицательные. Числа могут быть «карликами» (например, масса атома), «гигантами» (например, масса земли), реальными (например, количество студентов в группе, рост, возраст). И каждое из чисел потребует для оптимального представления в памяти свое количество байтов.

Единого оптимального представления для действительных чисел создать невозможно. Поэтому множества чисел разделили на типы (например, целые в диапазоне от … до …, приближенные с плавающей точкой с количеством значащих цифр … и т.д.). Для каждого в отдельности типа создается собственный способ представления.

Целые числа. Целые положительные числа от 0 до 255 можно представить непосредственно в двоичной системе счисления (двоичном коде). Такие числа будут занимать один байт в памяти компьютера.

Числа	Двоичный код
…	……..

В такой форме представления на компьютере легко реализуется двоичная арифметика. Знак числа «плюс» или «минус» кодируется отдельным битом. Обычно это старший бит. Ноль интерпретируется, как «плюс», единица - как «минус». Таким образом, одним байтом могут быть закодированы целые числа в интервале от –128 до +127. Двоичная арифметика при этом будет несколько усложнена, т.к. в этом случае существуют два кода, изображающих число ноль 00000000 и 100000000. В компьютере на аппаратном уровне это необходимо предусмотреть. Данный способ представления целых чисел называется прямым кодом. С отрицательными числами несколько проще, если использовать дополнительный код. В дополнительном коде положительные числа совпадают с положительными числами в прямом коде, отрицательные же числа получаются в результате вычитания из 100000000 соответствующего числа. Например, число –3 получит код:

_100000000

11111101

В дополнительном коде хорошо реализуется арифметика. Каждый последующий код получается из предыдущего прибавлением единицы с точностью до бита в девятом разряде. Например, 5 – 3 = 5 + (-3)

+11111101

100000010

Отбрасывая подчеркнутый старший разряд, получим 2.

Аналогично целые числа от 0 до 65536 и целые числа от –32768 до 32767 в двоичной (шестнадцатеричной) системе счисления представляются в двухбайтовых ячейках. Существуют представления целых чисел и в четырехбайтовых ячейках.

Действительные числа. Действительные числа в математике представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Однако, в компьютере числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разрядов. Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в компьютерном представлении выступают как приближенные. В большинстве систем программирования целая и дробная части в написании действительных чисел разделяются не запятой, а точкой.

Для представления действительных чисел, как очень маленьких, так и очень больших, удобно использовать форму записи чисел в виде произведения:

X = mq^p ,

Где m- основание системы счисления;

P – целое число, называемое порядком.

Такой способ записи чисел называется представлением числа с плавающей точкой.

Т.е. число 1234,56 может быть записано:

1234,56 = 123,456*10¹ = 12,3456*10² = 1,23456*10³ = 0,123456*10⁴.

Такое представление не однозначно. Если мантисса 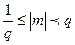(0,1 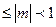для десятичной С.С.), то представление числа становится однозначным, а такая форма называется нормализованной. Если «плавающая» точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т.е., максимальная точность.

Действительные числа в компьютерах различных типов записываются по-разному, но существует несколько стандартных международных форматов, различающихся по точности, но имеющих одинаковую структуру. Рассмотрим на примере 4 байтного числа.

Смещенный порядок

Мантисса

Знак

мантиссы

Первый разряд представления используется для записи знака мантиссы. За ним – группа разрядов, определяющих порядок, а остальные разряды определяют абсолютную величину мантиссы. Размеры обеих групп разрядов фиксируются. Т.к. порядок может быть положительным или отрицательным, нужно решить проблему его знака. Величина порядка представляется с избытком, т.е., вместо истинного значения порядка хранится число, называемое характеристикой (или смещенным порядком). Для получения характеристики надо к порядку прибавить смещение. Например, при использовании для хранения порядка восьми бит и значений от –128 до +127 используется смещение 128. Тогда для представления порядка будут использоваться значения от 0 до 255, т.е. только неотрицательные числа.

Т.к. мантисса нормализованного числа всегда равна 1, некоторые схемы представления ее лишь подразумевают, используя лишний разряд для повышения точности представления мантиссы.

Использование смещенной формы позволяет производить операции над порядками, как над без знаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков. А также упрощает операцию сравнения самих нормализованных чисел. Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего, отличного от нуля числа до наибольшего числа, представимого в компьютере при заданном формате.

Как и в случае целых чисел, в программных системах могут использоваться несколько типов данных, реализующих модель с плавающей точкой. Например, в языке СИ применяются три типа данных с разной «длиной». Шестнадцатиразрядные компиляторы для IBM-совместимых ПК реализуют эти типы следующим образом:

Float – 4 байта, из них 23 разряда мантиссы и 8 битов порядка

(от 3,4*10^-38 до 3,4*10³⁸, обеспечивает точность с 7 значащими цифрами);

Double – 8 байтов, из них 52 разряда мантиссы и 11 битов порядка

(от 1,7*10^-308 до 1,7*10³⁰⁸, обеспечивает точность с 15 знаками);

Long double – 10 байтов, из них 65 разрядов мантиссы и 14 битов порядка

(от 3,4 * 10^-4932, обеспечивает точность с 19 знаками).

Понятие типа данных. Мы уже говорили, что минимально адресуемой единицей памяти является байт, но представление числа требует большего объема. Такие числа займут группу байт, а адресом числа будет адрес первого байта группы. Следовательно, произвольно взятый из памяти байт ничего не скажет о том, частью какого информационного объекта от является – целого числа,числа с плавающей точкой или командой. Отсюда можно сделать вывод, что кроме задачи представления данных в двоичном коде, параллельно решается обратная задача – интерпретации кодов, т.е. как из кодов восстановить первоначальные данные.

Для представления основных видов информации (числа целые, числа с плавающей точкой, символы, звук и т.д.) в системах программирования используют типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных.