Область видимости процедур

В начале заголовка процедуры, т.е. перед словом Sub или Function, может указываться слово Private или Public, задающее область видимости процедуры:

-Private: процедура может вызываться только из процедур того модуля, в котором она находится;

-Public: процедура может вызываться из процедур как того модуля, в котором она находится, так и других модулей.

Если область видимости не указана, то по умолчанию предполагается видимость процедуры во всех модулях (т.е. область видимости, соответствующая слову Public). Если программа состоит только из одного модуля, то область видимости процедур этой программы никак не влияет на ее работу.

Варианты заданий.

Вариант 1. В программе вводится двумерный массив. Вычисляется среднее по каждой строке, а также среднее по всему массиву. Составляются два новых массива. Первый из них включает те строки исходного массива, для которых среднее значение превышает среднее по массиву, второй – все остальные строки исходного массива. Вычисление среднего по строке массива должно быть реализовано в виде отдельной процедуры.

Вариант 2. В программе вводится двумерный массив. Из него должны удаляться все строки и столбцы, состоящие только из нулей. Проверка строк и столбцов (с целью выяснить, состоит ли данная строка или столбец только из нулей) должна выполняться с помощью отдельных процедур.

Вариант 3. В программе вводятся два массива: двумерный (обозначим его как a) и одномерный (b), причем количество элементов в одномерном массиве должно быть равно количеству строк в двумерном массиве. Для каждого элемента массива b определяется ближайший к нему элемент в соответствующей строке массива a (т.е. элемент, разность с которым минимальна). Поиск ближайшего элемента должен быть реализован в виде отдельной процедуры. Из номеров этих ближайших элементов составляется одномерный массив.

Вариант 4. В программе вводится двумерный массив. Из него должен составляться новый массив, включающий только те строки исходного массива, которые состоят из одинаковых чисел. Проверка строк (с целью выяснить, состоит ли данная строка из одинаковых чисел) должна выполняться с помощью отдельной процедуры.

Вариант 5. В программе вводится двумерный массив. В каждой строке определяется максимальное и минимальное число, и вычисляется их разность. Строка, где эта разность максимальна, должна меняться местами со строкой, где разность минимальна. Определение минимального и максимального значения в строке должно быть реализовано в виде отдельной процедуры.

Вариант 6. В программе вводится двумерный массив. Из него составляются два новых массива: в первый из них включаются те строки исходного массива, где нет ни одного отрицательного числа, во второй – те строки, где есть хотя бы одно отрицательное число. Проверка строки на наличие отрицательного числа должна быть реализована в виде отдельной процедуры.

Вариант 7. В программе вводится двумерный массив. В каждой строке вычисляется среднее значение. Составляется новый массив, содержащий столько же строк, что и исходный массив. Строки нового массива составляются из элементов соответствующей строки исходного массива, превосходящих среднее значение по своей строке. Так как количество элементов, отбираемых из каждой строки, оказывается при этом разным, недостающие элементы в конце строк нового массива остаются равными нулю. Вычисление среднего по строке массива должно быть реализовано в виде отдельной процедуры.

Вариант 8. В программе вычисляется значение функции sh x (гиперболический синус) на основе ее представления в виде ряда Тейлора: 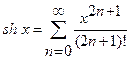. Значение переменной x, а также требуемая точность вводятся с клавиатуры. Вычисление ряда Тейлора должно быть реализовано в виде функции (вызывающая процедура должна содержать только ввод исходных данных, вызов функции и вывод результата).

Вариант 9. В программе вводится квадратная матрица (обозначим ее как a) и некоторое число s. Элемент матрицы a(1,1) сравнивается с числом s. Если a(1,1) > s, то программа завершает работу. В противном случае вычисляется сумма элементов квадратной матрицы 2x2 из левого верхнего угла матрицы a. Если эта сумма снова оказывается меньше s, то вычисляется сумма матрицы 3x3, и т.д., пока не будет достигнута сумма, превышающая s. Вычисление суммы квадратной матрицы, выделенной из исходной матрицы a, должно быть реализовано в виде функции. Программа должна выводить на экран размерность квадратной матрицы, сумма которой превысила s. Если число s не превышено при суммировании всей матрицы a, то должно выводиться сообщение об ошибке.

Вариант 10. В программе вводится одномерный массив a, состоящий из целых чисел, не превышающих 100. Вводятся также два числа: g (вводится значение 100) и k (некоторое произвольное целое число). В программе подсчитывается количество элементов массива a, превышающих величину g. Если это количество составляет не меньше k, то программа завершает работу; при этом из чисел, превышающих g, составляется новый массив. В противном случае величина g уменьшается на 0,5, и проверка повторяется. Подсчет количества элементов массива, превышающих заданную границу g, должен быть реализован в виде функции.

Вариант 11. В программе вводится одномерный массив a, и некоторое число s. Вычисляется среднее значение элементов массива (если в массиве есть элементы, равные нулю, то при вычислении среднего они не учитываются). Если среднее значение превышает s, то программа завершает работу; при этом из ненулевых элементов массива a составляется новый массив. В противном случае в массиве определяется минимальное число, оно заменяется на ноль, снова вычисляется среднее, и проверка повторяется. Если заданное среднее значение не достигается после исключения всех элементов массива, то выводится соответствующее сообщение.

Вариант 12. В программе вычисляется интеграл от некоторой функции y = f(x) на отрезке [a, b] на основе метода левых прямоугольников. Для этого отрезок [a, b] разбивается на k участков одинаковой длины d=(b-a)/k, т.е. определяются точки x₀ = a, x₁ = a+d, x₂=a+2d, …, x_k-1 = a+(k-1)d. Вычисляются значения функции y в этих точках: y₀ = f(x₀), y₁ = f(x₁), …, y_k-1 = f(x_k-1). Оценка интеграла вычисляется как (y₀+y₁+…+y_k-1)·d. Затем k увеличивается на единицу, и вычисление повторяется. Процесс завершается, когда разность оценок интеграла при двух последовательных значениях k оказывается меньше заданной точности. Требуется разработать программу для вычисления интеграла от функции 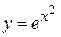этим методом. В программе должны запрашиваться границы отрезка (a и b), а также требуемая точность. Начальное значение k задается в программе (например, k=2). Непосредственно алгоритм вычисления интеграла должен быть реализован в виде функции.

Вариант 13. В программе определяется решение некоторого уравнения f(x) = 0 на отрезке [a, b] методом дихотомии. Для применения этого метода необходимо выбрать точки a и b таким образом, чтобы величины f(a) и f(b) имели разные знаки. Определяется середина этого отрезка c = (b+a)/2, и в этой точке вычисляется значение f(c). Если это значение отличается от нуля на величину, не превышающую заданной точности, то задача решена (c – решение). В противном случае отрезок [a, b] разбивается пополам. Выбирается тот из двух полученных отрезков, на концах которого исследуемая функция f(x) принимает разные знаки, и для этого отрезка процесс повторяется. Требуется разработать программу для решения уравнения sin x / x = 0 этим методом. В программе должны запрашиваться границы отрезка (a и b), а также требуемая точность. Непосредственно алгоритм решения уравнения должен быть реализован в виде функции.

Вариант 14 – В программе вводятся два одномерных массива (обозначим их как a и b), причем известно, что сумма массива a меньше суммы массива b (если это не так, то должно выводиться сообщение об ошибке). Составляется новый одномерный массив c. Сначала в него включаются все элементы массива a; затем к нему добавляются элементы массива b, начиная с b(1), до тех пор, пока сумма массива a не превысит сумму оставшихся элементов массива b. Суммирование элементов массива должно быть реализовано в виде функции. На экран выводится полученный массив c.

Контрольные вопросы.

1. Что представляет собой программа VBA?

2. Что включает в себя структура среды разработки IDE (редактор VBA)?

3. Какие области включает в себя каждый модуль программы VBA?

4. Дайте определение линейной программы VBA.

5. Поясните, как используются комментарии в программах.

6. Изложите структурупрограммы-процедуры на VBA.

7. Изложите структурупрограммы–функции на VBA.

Оформление отчета

Отчет по лабораторной работе должен содержать:

Титульный лист.

2. Цели работы.

3. Краткие теоретические сведения в виде ответов на контрольные вопросы.

4. Результаты лабораторной работы (графики, таблицы, значения параметров измеренных в процессе работы).

5. Необходимые расчеты (если они оговариваются в практической части лабораторной работы).

6. Выводы по работе (что получено в процессе работы, почему получены данные результаты и т. д.).

7. Отчет для защиты представляется преподавателю в отпечатанном или электронном виде.

Литература

1. Гарнаев А. Ю. Самоучитель VBA. / А. Ю. Гарнаев. – СПб.: БХВ-Петербург, 2003. – 512с.

2. Демидова Л. А. Программирование в среде Visual Basic for Applications: Практикум. / Демидова Л.А. , Пылькин А.Н. – М.: Горячая линия – Телеком, 2004. – 176 с.

3.Воробьева Ф.И., Воробьев Е.С. Приемы программирования в среде Visual Basic for Application MS Office. – Казань: Изд-во Казан. гос. технол. ун-та, 2010. – 104 с.

4. Любин А.Н. Создание пользовательских форм в Visual Basic for Applications. – М.: Изд-во Московского государственного технического университета «МАМИ», 2012. – 60 с.