Формирование математической модели. X(n) – одномерный массив;
Исходные данные
a = 0,96;
b = 35,
n £ 10;
m £ 15.
X(n) – одномерный массив;
xi – значение i-го элемента;
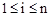– диапазон изменения индекса i;
i = i + 1 – шаг изменения индекса i.
Примем n = 5, зададимся x1=4,5; x2=12,3; x3=-0,8; x4=17; x5=0,3
Y(m) – одномерный массив;
yj – значение j-го элемента;
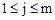– диапазон изменения индекса j;
j = j + 1 – шаг изменения индекса j.
Примем m = 4, зададимся y1=45,3; y2=-0,3; y3=12,7; y4=2,5
Расчетные зависимости
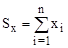– сумма элементов массива Х;
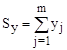– сумма элементов массива Y;
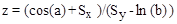– результат вычислений.
Выбор метода решения
Анализ математической модели задачи определяет необходимость подпроцесса – двукратного вычисления суммы элементов массивов (X и Y) различных размеров (n и m). Вычисление суммы, как известно, реализуется типовой универсальной методикой на любое число слагаемых – предписывает использование дополнительного смешанного подпроцесса двукратного получения одного результата – суммы элементов одномерного массива. Особенность задачи – необходимость передачи в дополнительный алгоритм, в качестве фактических параметров, одномерных массивов, вначале X(n), а затем Y(m). Математическое обозначение каждого массива содержит два элемента: имя и размер, позволяя передавать их отдельно. Для их получения в дополнительном алгоритме в качестве формальных параметров зададимся именем массива Т и размером k.
Назвав подпроцесс sum, запишем два обращения к нему:
sum( X, n), sum( Y, m).
В первом фактическими параметрами являются имя массива X и его размер n, во втором – Y и m.
Следовательно, рациональный метод решения задачи – вычислительный процесс с одним подпроцессом при использовании основного алгоритма с указанием в обращениях параметров одномерных массивов X(n) и Y(m).
Составление алгоритма решения
С учётом выбранных обозначений схемы основного и дополнительного алгоритмов представлены на рис. 10.12.
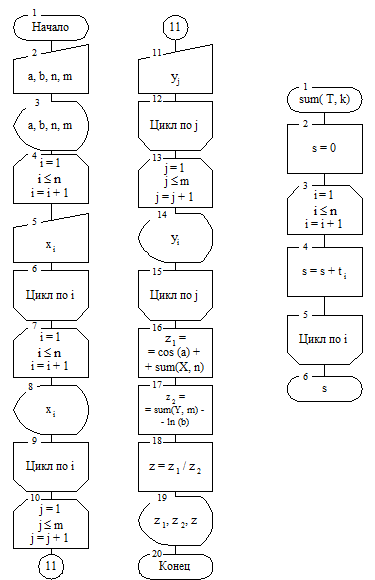
Рис. 10.12. Схемы основного и дополнительного алгоритмов задачи о сумме элементов одномерных массивов
Используемые в дополнительном алгоритме переменные s и i являются локальными.
Программирование задачи
Особенность рассматриваемой задачи – необходимость использования в качестве формальных и фактических параметров имен и размеров массивов.
В языке Си/Си++ передача массива в вызываемую функцию предписывает в качестве фактических параметров указать адрес расположения массива в оперативной памяти и фактический размер массива.
Следовательно, обращение для передачи массива X(n), имеет вид sum( x , n ), а для массива Y(m) – sum(y, m).
ü Внимание! В списке фактических параметров идентификатор одномерного массива однозначно подразумевает адрес его первого элемента.
Таким образом, имя массива может быть заменено адресом его первого элемента, т. е. рассмотренные обращения можно записать как sum( &x[0] , n ) и sum( &y[0] , m ).
Для приема значений фактических параметров, передаваемых в виде адреса, в списке формальных параметров используются указатели.
Указатель – переменная для хранения адреса операнда.
Физически указатель есть поименованная ячейка оперативной памяти, предназначенная для хранения адреса других переменных и массивов. Таким образом, указатель отличается от простой переменной только типом хранимой константы – адресом. Полное название – указатель на переменную.
Указатели, как и простые переменные, обозначаются именами (идентификаторами). Имена задаются самим пользователем по обычным для переменных правилам.
Описываются указатели аналогично переменным и массивам. Тип указателя определяется типом переменной (массива), на которую он ссылается.
Структура описания указателя:
описатель * иу1 [, * иу2, . . . , * иуN ];
где описатель – ключевое слово, определяющее тип указателя;
* – признак указателя при описании;
иу1... иуN – идентификаторы указателей;
, – разделитель списка идентификаторов;
[ ] – признак необязательности содержимого;
; – символ окончания оператора.
Описание указателей производится в начале программы (функции) аналогично простым переменным и массивам. При этом используются отдельные операторы описания или в списках уже существующих (наряду с переменными и массивами) указываются имена указателей с предшествующими им звездочками.
Например, описатели
float *a, *b;
int *f;
описывают два указателя на вещественные переменные, адреса которых будут указаны в ячейках с именами a и b, и один – на целую переменную, адрес которой можно хранить в ячейке f.
Описатели
float x, y, *a, *b;
int *f, arr[10];
наряду с указателями задают типы переменных x, y и целочисленного массива arr. В списке совместного описания месторасположение указателя задается произвольно.
Соответствие указателя и адреса переменной, на которую он ссылается, выражается зависимостью
иу = &ип
где иу – идентификатор указателя;
& – операция взятия адреса;
ип – идентификатор переменной.
Так, при выполненном ранее описателе
float x, y, *a, *b;
оператор
b = &x;
предписывает указателю на переменную вещественного типа b хранение адреса вещественной переменной x.
Операторы
f = &arr[0]; или f = arr;
задают указателю f значение адреса массива arr (его первого элемента).
Указатели позволяют не только хранить адреса переменных, но и вызывать в случае необходимости их содержимое с помощью операции разадресации.
Разадресация – получение содержимого операнда (переменной, ячейки оперативной памяти), на которую ссылается указатель.
Разадресация выполняется указанием символа звездочка (*) перед именем указателя.
Структура разадресации:
*иу
где иу – идентификатор указателя;
* – символ операции разадресации.
ü Внимание! Несмотря на совпадение форм записи описания указателей и разадресации, назначения их абсолютно различны и определяются месторасположением в программе (описателях или выполняемых участках). Операция разадресации, как правило, позволяет сформировать (получить/записать) операнд выражения или фактического параметра.
Так, фрагмент программы использования операции разадресации для получения значения
float g, s, *t;
. . .
g = 15.3;
t = &g;
s = sqrt( *t ) + *t + 0.5;
. . .
описывает переменные g, s и указатель t как вещественные, присваивает указателю t адрес переменной g, а затем, используя операцию разадресации указателя t, формирует операнды выражения s – подкоренное выражение и второе слагаемое – как константы 15.3 (содержимое переменной g).
Фрагмент
float x, z, *d;
. . .
d = &z;
*d = pow( x , 2 ) + 5;
. . .
поясняет использование операции разадресации для записи константы (результата вычисления выражения pow( x , 2 ) + 5) в ячейку переменной z с использованием указателя d.
ü Внимание! В работе с дополнительными функциями указатели используются как элементы списка формальных параметров. При этом в списке фактических параметров им должны соответствовать адреса переменных (массивов).
Использование массивов в вызове дополнительной функции требует указания двух фактических параметров каждого (имени и размера). При этом в заголовке вызываемой функции описываются в качестве формальных параметров пары (указатель и целая переменная) для каждого массива. В дополнительной функции описание принимающих массивов не требуется.
Элементы переданного в дополнительную функцию массива могут использоваться напрямую (указанием индексного выражения) или с помощью операции разадресации.
Так, фрагменты программы
| . . . float funk( float *px , int n1 ); main( ) { float t, x[10]; . . . n = 10; t = funk( x , n ); . . . } float funk( float *px, int n1 ) { . . . for( i=0 ; i <= n1 ; i++ ) f = . . . + px[i] + . . . .; . . . return f; } | . . . float funk( float* , int ); main( ) { float t, x[10]; . . . n = 10; t = funk( x , n ); . . . } float funk( float *px, int n1 ) { . . . for( i=0 ; i <= n1 ; i++ ) f = . . . + *(px+i) + . . . .; . . . return f; } |
поясняют варианты передачи одномерных массивов в функцию, использования её элементов и способы написания прототипа. В правом варианте прототипа тип указателя дополнен обязательным элементом – знаком «*».
В дополнительной функции вызов i-го элемента массива осуществляется двумя способами:
· индексированной переменной;
· полным индексным выражением.
В любом случае имя указателя идентифицирует массив (адрес первого элемента), а индекс i – смещение текущего элемента относительно первого. Первый способ предписывает вызов значения текущего элемента массива через автоматически сформированный адрес, а второй – через операцию разадресации.
Для одномерных массивов в большинстве случаев используют первый способ как более привычный и компактный.
С учетом изложенного, идентификация переменных задачи представлена в табл. 10.2:
Таблица 10.2
| Обозначение в алгоритме | a | b | n | m | i | j | xi | yj | z1 | z2 | z | k | ti | s |
| Обозначение в программе | a | b | n | m | i | j | x[i] | y[j] | z1 | z2 | z | k | t[i] | s |
Классический вариант программирования задачи
#include<stdio.h>/*файл с прототипами функций ввода-вывода*/
#include<conio.h/*файл с прототипом функций getch(), clrscr()*/
#include <math.h> /*файл с прототипами математич. функций*/
#include<windows.h> /*файл с прототипом функции CharToOem*/
float sum(float *t, int k);/*прототип пользовательской функции*/
main( ) /* заголовок головной функции */
{
float a, b, z1, z2, z, x[10], y[15]; /* описатели локальных */
int i, j, n, m; /* переменных и массивов */
char buf[30];
clrscr( );
CharToOem(" Введите значения a, b, n, m: ",buf);
printf("\n %s \n",buf);
scanf("%f%f%d%d", &a, &b, &n, &m);
printf("\n a=%.2f b=%.2f n=%d m=%d\n", a, b, n, m);
for( i = 0 ; i < n ; i++ ) /* заголовок цикла ввода x[ i ] */
{
CharToOem(" Введите значение ",buf);
printf("\n %s x(%d): ",buf,i+1);
scanf("%f", &x[i]);
}
for( i = 0 ; i < n ; i++ ) /* заголовок цикла вывода x[ i ] */
printf(" %.2f",x[i]);
printf("\n"); /* перевод курсора в начало следующей строки */
for( j = 0 ; j < m ; j++ ) /* заголовок цикла ввода y[ j ] */
{
CharToOem(" Введите значение ",buf);
printf("\n %s y(%d): ",buf,j+1);
scanf("%f", &y[j]);
}
for( j = 0 ; j < m ; j++ ) /* заголовок цикла вывода y[ j ] */
printf(" %f",y[j]);
z1 = cos(a) + sum( x, n ); /* вычисление с обращением к */
z2 = sum( y , m ) - b; /* дополнительным функциям */
z = z1 / z2;
printf("\n\n z1=%.2f z2=%.2f z=%.2f\n", z1, z2, z);
getch( );
}
/* определение дополнительной функции расчёта суммы элементов одномерного массива */
float sum(float *t, int k) /*заголовок дополнительной функции*/
{
float s; /* описание локальных */
int i; /* переменных s и i */
s = 0;
for( i = 0 ; i < k ; i++ ) /* заголовок цикла расчета суммы */
{
s = s + t[ i ];
}
return s; /*возвращение значения s в вызывающую функцию*/
}
0.96 35. 5 4
4.5 12.3 -0.8 17 0.3
45.3 -0.3 12.7 2.5
Под закрывающей скобкой приведены исходные данные для решения задачи.
Результаты решения представлены в приложении 10.3.
Программирование задачи с графическим интерфейсом
Программирование задачи при использовании графического интерфейса предварим его разработкой. Для ввода значений a, b, n, m планируем однострочные поля редактирования (EditA, EditB, EditN, EditM). Для ввода элементов массивов X и Y используем многострочные поля редактирования (EditХ, EditY).
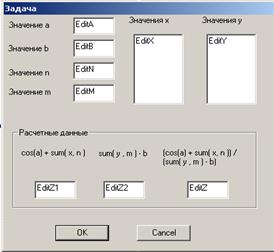
Вывод расчетных значений z1, z2, z реализуем в однострочные поля редактирования (EditZ1, EditZ2, EditZ).
Управление процессом решения реализуем двумя командными кнопками, расположенными в нижней части окна. Назначение каждой определяется ее названием.
С учетом планируемого интерфейса выполним программирование задачи.
#include <stdio.h>/*файл с прототипами функций ввода-вывода*/
#include <math.h>/*файл с прототипами математич. функций*/
float sum(float *t, int k);/*прототип пользовательской функции*/
…
void TSumprDlgClient::BNClickedOk()
{
// INSERT>> Your code here.
float a, b, z1, z2, z, x[10], y[15]; /* описатели локальных */
int i, j, n, m; /* переменных и массивов */
char buf[30];
EditA->GetText(buf,10); /*ввод */
a=atof(buf); /*значения а*/
EditN->GetText(buf,10); /*ввод */
n=atoi(buf); /*значения n*/
EditM->GetText(buf,10); /*ввод */
m=atoi(buf); /*значения m*/
EditB->GetText(buf,10); /*ввод */
b=atoi(buf); /*значения b*/
for( i = 0 ; i < n ; i++ ) /* заголовок цикла ввода x[ i ] */
{
EditX->GetLine(buf, sizeof(buf),i);
x[i]=atof(buf);
}
for( j = 0 ; j < m ; j++ ) /* заголовок цикла ввода y[ j ] */
{
EditY->GetLine(buf, sizeof(buf),j);
y[j]=atof(buf);
}
z1 = cos(a) + sum( x, n ); /* вычисления с обращением к */
z2 = sum( y , m ) - b; /* дополнительной функции */
z = z1 / z2;
sprintf(buf,"%.2f ",z1); /* вывод */
EditZ1->SetText(buf); /*значения z1*/
sprintf(buf,"%.2f ", z2); /* вывод */
EditZ2->SetText(buf); /* значения z2*/
sprintf(buf,"%.2f",z); /* вывод */
EditZ->SetText(buf); /* значения z*/
}
float sum(float *t, int k) /*заголовок дополнительной функции*/
{
float s; /* описание локальных */
int i; /* переменных s и i */
s = 0;
for( i = 0 ; i < k ; i++ ) /* заголовок цикла расчета суммы */
s = s + t[ i ];
return s; /*возвращение значения s в вызывающую функцию*/
}
0.96 35. 5 4
4.5 12.3 -0.8 17 0.3
45.3 -0.3 12.7 2.5
Под закрывающей скобкой приведены исходные данные для решения задачи.
Результаты решения представлены в приложении 10.4.