Закон всемирного тяготения
Лабораторная работа № 161. Измерение ускорения свободного падения с помощью математического маятника
Введение
Ускорением свободного падения g называется ускорение относительно Земли, c которым свободное тело начинает падать. Это ускорение определяется суммой силы гравитационного притяжения Земли и центробежной силы инерции.
Математическим маятником называется гипотетический маятник, вся масса которого сосредоточена в одной точке, а расстояние до точки подвеса l не меняется при колебаниях. Простые расчеты показывают, что при небольших углах отклонения от вертикали период этого маятника удовлетворяет соотношению:
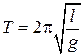 (1)
(1)
Отсюда ясна идея одного из способов определения ускорения свободного падения. Необходимо измерить длину и период математического маятника.
Однако возникает вопрос: описываются ли свойства реального маятника моделью математического маятника?
Здесь стоит заметить, что выражение (1) утверждает прямую пропорциональность периода колебаний математического маятника от 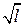 . Значит, если будет выяснено, что для нашего маятника такая зависимость имеет место, его можно считать математическим и определить ускорение свободного падения по формуле
. Значит, если будет выяснено, что для нашего маятника такая зависимость имеет место, его можно считать математическим и определить ускорение свободного падения по формуле
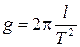 (2)
(2)
Приступая к работе необходимо
Знать определения
вектора и составляющей вектора;
координат вектора;
проекции вектора на направление;
вектора угла бесконечно малого поворота, угловой скорости, углового ускорения;
системы координат и системы отсчета;
инерциальной и неинерциальной систем отсчёта;
массы тела, момента инерции тела;
силы, момента силы;
центра масс;
силы инерции;
ускорения свободного падения;
силы тяжести.
Знать
формулировку и границы применения уравнения динамики вращательного движения;
выражения для сил инерции;
уравнение движения материальной точки относительно земной вращающейся системы отсчета;
причины зависимости ускорения свободного падения от положения на поверхности Земли.
Уметь
измерять расстояния с помощью линейки;
измерять время ручным секундомером;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Измерение ускорения свободного падения.
Решаемые задачи
ü Знакомство с методом измерения ускорения свободного падения методом математического маятника;
ü Оценка адекватности описания имеющегося маятника моделью математического маятника;
ü Измерение ускорения свободного падения.
Экспериментальная установка
Приборы и принадлежности:
ü Массивный шар, подвешенный на труднорастяжимом шнуре;
ü Рулетка;
ü Секундомер.
Порядок выполнения работы
1. Укоротите шнур так, чтобы его длина между шариком и стальным кольцом равнялась бы 3-5 см. Высвободившийся конец шнура намотайте на крюк;
2. Измерьте длину маятника l – расстояние от точки подвеса до центра шара;
3. Отклоните шар так, чтобы шнур составлял с вертикалью угол не более 10° и отпустите шар;
4. Измерьте время 10 полных колебаний t10 и найдите период колебаний T= t10/10;
5. Увеличьте длину маятника на 5-10 см, смотав с крючка несколько витков шнура;
6. Повторите пп 2-4;
7. Повторяйте пп 5-6 до тех пор, пока длина маятника не превзойдёт 100 см.
Обработка и представление результатов
По результатам измерений, и проведя вычисления, заполните таблицу.
| N | l, см | 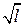 , см1/2 , см1/2 | t10, с | T, с |
| … |
Постройте график зависимости T( 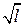 ). Выделите на нём линейный участок. По точкам этого участка, пользуясь выражением (2) найдите ускорение свободного падения.
). Выделите на нём линейный участок. По точкам этого участка, пользуясь выражением (2) найдите ускорение свободного падения.
Лабораторная работа № 162. Измерение ускорения свободного падения с помощью оборотного маятника
Введение
Ускорением свободного падения g называется ускорение относительно Земли, c которым свободное тело начинает падать. Это ускорение определяется суммой силы гравитационного притяжения Земли и центробежной силы инерции.
Для определения ускорения gможно воспользоваться физическим маятником. Физическим маятником называется абсолютно твердое тело, которое может качаться вокруг неподвижной горизонтальной оси. При отсутствии силы трения уравнение движения маятника выглядит следующим образом:
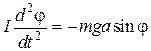 , (1)
, (1)
где m - масса тела, I - момент инерции относительно точки подвеса, a - расстояние от точки подвеса до центра тяжести, j - угол отклонения маятника от положения равновесия. В случае малых колебаний в этом уравнении можно заменить sin j на j. В результате получим уравнение гармонического колебания с периодом:
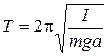 (2)
(2)
Частным случаем физического маятника является математический маятник. Так называется гипотетический маятник, вся масса которого сосредоточена в одной точке. В этом случае формула (2) упрощается (так как I = ml2 ,a = l, где l -длина маятника) и для ускорения свободного падения получим:
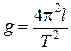 (3)
(3)
Отсюда ясна идея одного из способов определения ускорения свободного падения. Необходимо измерить длину и период математического маятника.
Сравнивая формулы (2) и (3), приходим к выводу, что физический маятник колеблется так же, как математический с длиной 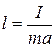 . Эта величина называется приведенной длинной физического маятника. Точка, удаленная от точки подвеса на расстояние l вдоль прямой, проходящей через центр масс, называется центром качания. Если маятник подвесить за центр качания, то период его колебаний не изменится (теорема Гюйгенса).
. Эта величина называется приведенной длинной физического маятника. Точка, удаленная от точки подвеса на расстояние l вдоль прямой, проходящей через центр масс, называется центром качания. Если маятник подвесить за центр качания, то период его колебаний не изменится (теорема Гюйгенса).
Важно иметь ввиду, что тот же самый период колебаний маятника может получиться при закреплении его, вообще говоря, в бесконечном множестве точек. Такие точки называются точками взаимности. Исходя из этого определения, центр качания и точка подвеса являются точками взаимности, но не единственно возможными. Поэтому расстояние между точками взаимности, которые легко установить по совпадению периодов колебаний, не всегда совпадает с приведенной длиной. Расстояние между точками взаимности равно приведенной длине физического маятника, только в том случае, если эти точки лежат на одной прямой с центром масс на разных расстояниях от него.
Приступая к работе необходимо
Знать определения
вектора и составляющей вектора;
координат вектора;
проекции вектора на направление;
вектора угла бесконечно малого поворота, угловой скорости, углового ускорения;
системы координат и системы отсчета;
инерциальной и неинерциальной систем отсчёта;
массы тела, момента инерции тела;
силы, момента силы;
центра масс;
сил инерции;
ускорения свободного падения;
силы тяжести.
Знать
формулировку и границы применения уравнения динамики вращательного движения;
выражения для сил инерции;
уравнение движения материальной точки относительно земной вращающейся системы отсчета;
причины зависимости ускорения свободного падения от положения на поверхности Земли.
Уметь
графически решать уравнения;
измерять расстояния с помощью линейки;
измерять время ручным секундомером;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Измерение ускорения свободного падения.
Решаемые задачи
ü Знакомство с методом измерения ускорения свободного падения методом оборотного маятника;
ü Измерение периода колебаний маятника;
ü Измерение ускорения свободного падения.
Экспериментальная установка
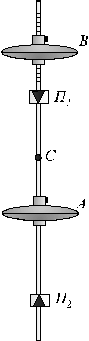 Рис. 1 Рис. 1 |
Приборы и принадлежности:
ü Оборотный маятник;
ü Рулетка;
ü Секундомер.
Оборотный маятник - устройство для определения ускорения свободного падения. Он состоит из стальной рейки, на которой жестко закреплены опорные стальные призмы П1 и П2 и массивное тело А, находящееся между ними (рис.1). Другое подобное тело В находится на одном из концов рейки (не между призмами). Оно может перемещаться по стержню и закрепляться в нужном положении. Перемещением этого тела достигают совпадения периодов колебаний маятника, когда точками подвеса являются ребра опорных призм П1 и П2. В этом случае ребра призм будут точками взаимности. Эти ребра закреплены асимметрично относительно центра масс С. Поэтому при совпадении периодов колебаний расстояние между ними дает приведенную длину физического маятника l. Измерив период его колебаний T, можно вычислить g по формуле (3).
Порядок выполнения работы
1. Рулеткой измерьте расстояние l между призмами.
2. Подвесьте маятник на одну из призм. Отклоните маятник на небольшой угол.
3. Отсчитайте как можно больше полных колебаний и определите по секундомеру время t, за которое они совершаются, рассчитайте период колебания T1.
4. Подвесьте маятник на другую призму и найдите период T2. При перевороте маятника старайтесь держать его как можно ближе к грузам.
5. Найдите периоды колебаний T1 и T2 для 7-10 положений чечевицы В.
6. На одном поле координат постройте графики зависимости периодов колебаний T1 и T2 от положения чечевицы.
7. Найдите точку пересечения графиков, определите период колебания в точке взаимности T = T1 = T2.
8. Рассчитайте g по формуле (3).
Обработка и представление результатов
По результатам измерений, и проведя вычисления, заполните таблицу.
| N | l, см | 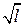 , см1/2 , см1/2 | t, с | T, с |
| … |
Постройте график зависимости T( 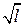 ). Выделите на нём линейный участок. По точкам этого участка, пользуясь выражением (2) найдите ускорение свободного падения.
). Выделите на нём линейный участок. По точкам этого участка, пользуясь выражением (2) найдите ускорение свободного падения.
Лабораторная работа № 163. Измерение гравитационной постоянной
Механические колебания
Лабораторная работа № 171. Пружинный маятник
Введение
Колебания осциллятора с затуханием описываются уравнением:
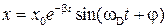 , (1)
, (1)
где 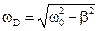 - циклическая частота затухающих колебаний, b - коэффициент затухания, w0 - циклическая частота собственных (т.е. незатухающих) колебаний. Это уравнение описывает не периодический процесс, но при b<<w0 можно считать, что это уравнение описывает гармоническое колебание с изменяющейся амплитудой
- циклическая частота затухающих колебаний, b - коэффициент затухания, w0 - циклическая частота собственных (т.е. незатухающих) колебаний. Это уравнение описывает не периодический процесс, но при b<<w0 можно считать, что это уравнение описывает гармоническое колебание с изменяющейся амплитудой 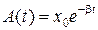 .
.
Таким образом, колебания осциллятора с затуханием характеризуются двумя параметрами b и w0. Однако зачастую, для удобства и информативности используют величины связанные с ними:
· Период колебаний T= 2p/wD ;
· Декремент затухания:
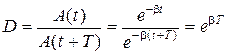 (2)
(2)
определяет отношение амплитуд колебаний, следующих друг за другом.
· Логарифмический декремент затухания:
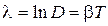 . (3)
. (3)
обратно пропорционален числу колебаний Ne, за которые амплитуда убывает в e раз (покажите).
· Добротность:
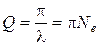 . (4)
. (4)
величина пропорциональная числу колебаний, за которое амплитуда сигнала уменьшается в e раз.
Чем выше добротность, тем медленнее в системе затухают колебания.
Величины декрементов затухания и добротности безразмерны. Они не зависят от выбора системы единиц, поэтому их использование более предпочтительно по сравнению с размерной величиной b.
В данной работе изучаются колебания пружинного маятника с целью установления общих закономерностей, свойственных осцилляторам с действующими диссипативными силами, проводится измерение параметров осциллятора.
Приступая к работе необходимо
Знать определения
гармонического осциллятора и осциллятора с затуханием;
амплитуды, частоты, фазы, начальной фазы, периода колебаний;
декремента затухания, логарифмического декремента затухания.
Знать
вид динамического и кинематического уравнений осциллятора и осциллятора с затуханием;
границы использования моделей гармонического осциллятора и осциллятора с затуханием.
Уметь
запускать программы в среде Windows и пользоваться стандартными элементами их интерфейса (меню, контекстные меню, окна и т.д.);
записывать уравнение движения груза, подвешенного на пружине и сводить его к уравнению осциллятора с затуханием;
решать уравнения гармонического осциллятора и осциллятора с затуханием;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы:
Изучение колебаний осциллятора с затуханием на примере пружинного маятника.
Решаемые задачи
ü наблюдение графиков зависимости смещения груза относительно положения равновесия от времени;
ü измерение периода колебаний;
ü определение декремента затухания колебаний пружинного маятника;
ü оценка зависимости периода колебаний и декремента затухания от амплитуды[1];
ü оценка вклада массы пружины в полную инертную массу маятника1.
Экспериментальная установка
Используемое оборудование
ü Штатив с установленным на нём держателем пружины и регистратором смещения – спицевым колесом со световыми воротами;
ü Две пружины (I – покороче, II – подлиннее);
ü Набор грузов;
ü Компьютерный интерфейс Sensor CASSY;
ü Компьютер с установленной программой CASSY Lab 2.
Порядок выполнения работы:
1. Включите Sensor CASSY и компьютер в сеть переменного тока 220В.
2. На Рабочем столе Windows найдите папку “Механика”. В ней найдите и стартуйте ярлык “Пружинный маятник”.
В открывшемся окне в строке инструментов найдите кнопку Measuring time. Щёлкая по ней, или нажимая на клавишу F9 можно запускать или останавливать измерения.!!! Перед каждым измерением необходимо сбрасывать координату SA1 на →0←. Для этого в строке меню нажмите правой кнопкой на SA1. Справа внизу во вкладке Setting\Path SA1 нажмите →0←.
3. Оттяните грузик на пружине вниз на 3 – 4 см (не больше!). Запустите измерения и отпустите грузик. На координатной сетке экрана при этом должна появиться затухающая синусоида, а в таблице слева – измеренные значения координат. После того, как синусоида выродится в прямую,параллельную оси ординат остановите измерения.
4. Если щёлкнуть мышкой по точке на графике, компьютер выделит соответствующее значение в таблице. Щёлкая мышкой последовательно по точкам максимумов, занесите в таблицу соответствующие им моменты времени ti и координаты по оси ординат si. В качестве нулевого выберите первый ярко выраженный экстремум.
Таблица:
| 1й эксп. | 2й эксп. | ||||
| φ | ti | si | Ti = tφ +2π - tφ | Di = sφ+2π/ sφ | ... |
| ... | |||||
| π | |||||
| 2π | |||||
| 3π | |||||
| ... |
5. Проведите эксперимент не менее трёх раз.
6. Повторите серии измерений для разного числа грузов (1, 2 и 3) и разного набора пружин (I и II последовательно). !!! Сохраните каждый эксперимент в файл (6 экспериментов) – для этого нажмите кнопку  или клавишу F2, выберите папку Документы\Students\выберите папку с номером вашей группы\Сохраните файл под своей фамилией и номером упражнения.
или клавишу F2, выберите папку Документы\Students\выберите папку с номером вашей группы\Сохраните файл под своей фамилией и номером упражнения.
Обработка и представление результатов
Данные измерений представьте в виде таблицы:
| m=M/M1 | T2I | T2II | T2экв= T2I+ T2II |
где М – общая масса всех грузов в i-ом эксперименте; М1 – масса грузика
Постройте графики зависимости T2 от относительной массы груза m.
Измерьте массу пружин mп и оцените её вклад в полную инертную массу маятника M+mп
Рассчитайте декременты затухания маятника.
Сделайте выводы о соответствии полученных данных предсказаниям теоретических расчётов.
Постройте графики зависимости периода колебаний от амплитуды.[2]
Постройте графики зависимости декремента затухания от амплитуды.2
Лабораторная работа № 172. Иучение свободных и вынужденных колебаний торсионного маятника
Введение
При небольших моментах сил трения колебания торсионного маятника описываются уравнением
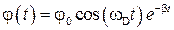 , (1)
, (1)
где φ0 – начальная амплитуда колебаний, 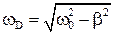 – циклическая частота затухающих колебаний, ω0 – собственная циклическая частота маятника, β – коэффициент затухания. В отсутствие сил трения (β = 0) колебания называются свободными.
– циклическая частота затухающих колебаний, ω0 – собственная циклическая частота маятника, β – коэффициент затухания. В отсутствие сил трения (β = 0) колебания называются свободными.
Коэффициент затухания β можно определить, зная декремент затухания D, который определяется отношением амплитуд:
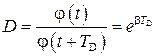 , (2)
, (2)
отличающихся на период колебаний 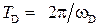 .
.
Логарифмируя выражение (2), получим логарифмический декремент затухания
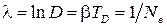 . (3)
. (3)
Ne – число колебаний, за которое угловая амплитуда убывает в e раз. Если через N колебаний угловая амплитуда уменьшается в k, то коэффициент затухания β можно определить из формулы
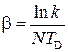 . (4)
. (4)
Таким образом, измерив TD и определив число 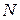 , когда угловая амплитуда уменьшилась в k раз, по формуле (4), можно вычислить β, а используя связь
, когда угловая амплитуда уменьшилась в k раз, по формуле (4), можно вычислить β, а используя связь
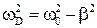 , (5)
, (5)
– определить собственную частоту ω0.
Приступая к работе необходимо
Знать определения
гармонического осциллятора и осциллятора с затуханием;
амплитуды, частоты, фазы, начальной фазы, периода колебаний;
декремента затухания, логарифмического декремента затухания.
Знать
вид динамического и кинематического уравнений осциллятора и осциллятора с затуханием;
границы использования моделей гармонического осциллятора и осциллятора с затуханием;
определение и физическую суть явления резонанса.
Уметь
записывать уравнение движения твёрдого тела под действием момента силы упругости и сводить его к уравнению осциллятора с затуханием;
решать уравнения гармонического осциллятора и осциллятора с затуханием;
оценивать случайные погрешности прямых и косвенных измерений.
Цели работы
Исследование свободных, затухающих и вынужденных колебаний торсионного маятника.
Решаемые задачи
ü Знакомство с основными понятиями физики колебаний;
ü Измерение собственной частоты торсионного маятника;
ü Определение коэффициента затухания торсионного маятника;
ü Построение графика зависимости частоты затухающих колебаний от логарифмического декремента затухания.
Экспериментальная установка
Приборы и принадлежности
ü торсионный маятник (1) с электромагнитом в виде катушки (5) и мотором, создающий вынуждающую осциллирую силу;
ü источник постоянного тока электромагнитной катушки торсионного маятника (2);
ü источник постоянного тока мотора маятника (4);
ü секундомер, кабели красный и синий 100 см.
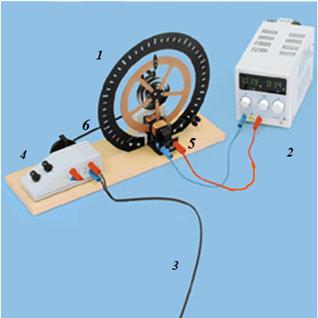 Рис.1. Торсионный маятник. Источник постоянного тока мотора (4) не показан. Рис.1. Торсионный маятник. Источник постоянного тока мотора (4) не показан. |
Торсионный маятник может использоваться для изучения свободных, и вынужденных вращательных гармонических колебаний. Электромагнитная катушка с током (5) тормозит (демпфирует) эти колебания. Тормозное воздействие будет тем больше, чем больший ток течёт по катушке. Кроме того, торсионный маятник может возбуждаться осциллирующей силой посредством эксцентрической тяги (6), (см. также, рис. 2) управляемой мотором. Число оборотов эксцентрической тяги мотора может меняться двумя ручками: грубой и точной настройки (4).
Порядок выполнения работы
Подготовка к эксперименту
1. В тетради, или в программе по обработке электронных таблиц создайте таблицу для записи данных эксперимента и результатов проведённых расчетов. Для этого прочитайте все описание до конца, и решите, какие данные необходимо внести в таблицу. Один из возможных вариантов такой:
| I, A | j0 | j10 | t10, с | 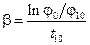 , с-1 , с-1 | ωD = 20p/t10, с-1 |
| I1 | |||||
| I2 | |||||
При проведении экспериментов заполняются первые 4 столбца, остальные – при проведении статистической обработки.
2. Включите источник постоянного тока (2) в сеть переменного тока 220 В. Дайте прибору прогреться 2-3 минуты.
3. Ручку А на источнике тока (2) установите в крайне правое положение.
Проведение эксперимента
4. Вращая ручку V на источнике тока (2), установите ток, подаваемый на электромагнит демпфирующей катушки, например, 0,2 А. При этом ручку А надо установить в крайне правое положение.
5. Отклоните белый указатель на маятнике на некоторый угол. Запишите угловую амплитуду j0. Отпустите указатель и измерьте время десяти полных колебаний t10. В конце десятого колебания измерьте угловую амплитуду j10.
6. Повторите пункты 3-4 несколько раз. По окончании всех измерений проведите статистическую обработку данных.
7. Увеличивая несколько раз ток в демпфирующей катушке, для каждого его значения повторите пункты 3-5. (Внимание! Величина тока на демпфирующей катушке не должна превышать 2 А)
Завершение эксперимента
8. Отключите электропитание приборов.
Обработка и представление результатов
Рассчитайте частоты затухающих колебаний ωD, и коэффициенты затухания β, и их погрешности.
Постройте график зависимости 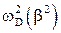 . Экстраполируя его к β = 0 (см. формулу (5)) найдите w0.
. Экстраполируя его к β = 0 (см. формулу (5)) найдите w0.
Литература
Савельев И.В. Курс общей физики: Учеб. Пособие для вузов. В 5 кн., Т.1., 1998, М., Физматлит.
Иродов И.Е. Механика. Основные законы. ‑ М.:БИНОМ. Лаборатория знаний, 2006.
Лабораторная работа № 173. Изучение явления резонанса торсионного маятника
Введение
Вынужденные колебания торсионного маятника возбуждаются моментом внешней силы с частотой ω и угловой амплитудой α0. Через интервал времени порядка 1/b маятник будет качаться на частоте ω с постоянной амплитудой, определяемой соотношением
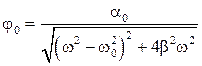 . (1)
. (1)
где ω0 – собственная циклическая частота маятника, β – коэффициент затухания.
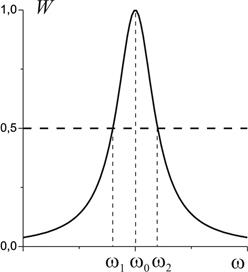 Рис. 1 Рис. 1 |
Зависимость (1) описывает явление резонансного возбуждения торсионного маятника. Если отобразить её в координатах W=(j/jмакс)2 и w, при выполнении условия b < ω0 получим следующее соотношение:
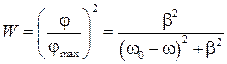 . (2)
. (2)
График этой зависимости изображен на рис. 1. Очевидно, что положение максимума резонансной кривой определяет величину w0. Проведем на графике прямую параллельную оси абсцисс при ординате 1/2. Эта прямая пересечет резонансную кривую в точках w1 и w2. Величину Dw = w2 - w1 называют шириной резонансной линии. Из (2) очевидно, что Dw = 2b. Таким образом, коэффициент затухания определяет полуширину резонансной линии.
Приступая к работе необходимо
Знать определения
гармонического осциллятора и осциллятора с затуханием;
амплитуды, частоты, фазы, начальной фазы, периода колебаний;
декремента затухания, логарифмического декремента затухания.
Знать
вид динамического и кинематического уравнений осциллятора и осциллятора с затуханием;
границы использования моделей гармонического осциллятора и осциллятора с затуханием;
определение и физическую суть явления резонанса.
Уметь
записывать уравнение движения твёрдого тела под действием момента силы упругости и сводить его к уравнению осциллятора с затуханием;
решать уравнения гармонического осциллятора и осциллятора с затуханием;
оценивать случайные погрешности прямых и косвенных измерений.
Цели работы
Исследование явления резонанса торсионного маятника.
Решаемые задачи
ü Знакомство с основными понятиями физики колебаний;
ü Исследование колебаний маятника от частоты вынуждающей силы и коэффициента затухания;
 Рис.1. Торсионный маятник. Источник постоянного тока мотора (4) не показан. Рис.1. Торсионный маятник. Источник постоянного тока мотора (4) не показан. |
ü Построение резонансных кривых;
ü Измерение собственной частоты торсионного маятника по резонансной кривой;
ü Определение коэффициента затухания торсионного маятника по резонансной кривой.
Экспериментальная установка
Приборы и принадлежности
ü торсионный маятник (1) с электромагнитом в виде катушки (5) и мотором, создающий вынуждающую осциллирую силу;
ü источник постоянного тока электромагнитной катушки торсионного маятника (2);
ü источник постоянного тока мотора маятника (4);
ü секундомер, кабели красный и синий 100 см.
Торсионный маятник может использоваться для изучения свободных, и вынужденных вращательных гармонических колебаний. Электромагнитная катушка с током (5) тормозит (демпфирует) эти колебания. Тормозное воздействие будет тем больше, чем больший ток течёт по катушке. Кроме того, торсионный маятник может возбуждаться осциллирующей силой посредством эксцентрической тяги (6), (см. также, рис. 2) управляемой мотором. Число оборотов эксцентрической тяги мотора может меняться двумя ручками: грубой и точной настройки (4).
Порядок выполнения работы
Подготовка к эксперименту
1. В тетради, или в программе по обработке электронных таблиц создайте таблицу для записи данных эксперимента и результатов проведённых расчетов. Для этого прочитайте все описание до конца, и решите, какие данные необходимо внести в таблицу. Один из возможных вариантов такой:
| I, A | N | tN, с | Dj0 | ωD = 2pN/tN, с-1 | (Dj0)2 |
| I1 | |||||
| I2 | |||||
При проведении экспериментов заполняются первые 4 столбца, остальные – при проведении статистической обработки.
2. Включите источник постоянного тока (2) в сеть переменного тока 220 В. Дайте прибору прогреться 2-3 минуты.
3. Ручку А на источнике тока (2) установите в крайне правое положение.
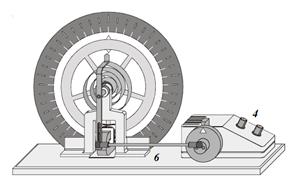 Рис. 2. Схематическое изображение маятника. Рис. 2. Схематическое изображение маятника. |
Проведение эксперимента
4. Вращая ручку V на источнике тока (2), установите ток, подаваемый на электромагнит демпфирующей катушки, 0,4 А.
5. Установите ручку грубой настройки (4) (см. рис. 2), например, в положение 10.
6. Измерьте секундомером время tN N штук полных оборотов эксцентрической тяги мотора (белый треугольник проходит указатель Nодин раз, см. рис. 2). Количество оборотов подбирайте так, чтобы tN было не менее 10 секунд. Занесите данные в таблицу.
7. Для этой частоты вынуждающей силы определите размах колебаний Dj0 (угол между крайними правым и левым положениями указателя на маятнике).
8. Повторите пункты 6-7 не менее пятнадцати раз, изменяя число оборотов эксцентрической тяги мотора, т.е. вращая ручки грубой и тонкой настройки (4) на рис.2.
9. Повторите пункты 5-8 еще не менее чем для двух значений тока в демпфирующей катушке, не превышая 2 А.
Завершение эксперимента
10. Отключите электропитание приборов.
Обработка и представление результатов
11. Проведите вычисления (Dj0)2 и ωD, заполнив соответствующие столбцы в таблице.
12. На одном координатном поле постройте графики зависимостей (Dj0)2 от ωD.
13. Соедините точки гладкими кривыми и определите значения (Dj0мах)2 в их максимумах
14. На одном координатном поле постройте графики зависимостей (Dj0/Dj0мах)2 от ωD.
15. По графикам найдите величины ω0 и b.
Литература
Савельев И.В. Курс общей физики: Учеб. Пособие для вузов. В 5 кн., Т.1., 1998, М., Физматлит.
Иродов И.Е. Механика. Основные законы. ‑ М.:БИНОМ. Лаборатория знаний, 2006.
Лабораторная работа № 174. Изучение колебаний связанных маятников
Введение
При произвольном возбуждении в системе двух связанных идентичных маятников возникает довольно сложное движение, характерной чертой которого является периодическая перекачка энергии от одного маятника к другому.
Тем не менее, можно показать, что такое движение является наложением двух строго периодических колебаний, которые можно возбудить независимо друг от друга. Такие колебания называют нормальными колебаниями (модами), а соответствующие им частоты – нормальными частотами системы.
В системе двух идентичных маятников нормальные колебания возбуждаются при отклонении на одинаковые углы в одну сторону (симметричное колебание) и при отклонении на одинаковые углы в противоположные стороны (антисимметричное колебание).
В симметричном колебании с угловой частотой ω+ меняется сумма двух углов отклонения маятников, а в антисимметричном с угловой частотой ω‑ – разница этих углов. (При этом отклонения в разные стороны от вертикали характеризуются углами с разными знаками).
Легко сообразить, что частота ω‑ больше, чем частота ω+, причём разница между этими частотами тем существенней, чем больше масса дополнительного груза и расстояние h от точек подвеса до точек закрепления нитей (докажите).
Достаточно полное изложение теории колебаний в системе связанных маятников и её обобщение на системы с большим числом степеней свободы можно найти в литературе [1,2].
Приступая к работе необходимо
Знать определения
гармонического осциллятора и осциллятора с затуханием;
амплитуды, частоты, фазы, начальной фазы, периода колебаний;
декремента затухания, логарифмического декремента затухания;
нормальных колебаний и нормальных частот.
Знать
вид динамического уравнения осциллятора;
вид системы уравнений, описывающих движение системы двух идентичных осцилляторов.
Уметь
сводить систему уравнений, описывающих движение системы двух идентичных осцилляторов, к независимым уравнениям, описывающим нормальные колебания;
измерять время секундомером;
измерять расстояния линейкой;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Знакомство с особенностями движения связанных осцилляторов
Решаемые задачи
ü Наблюдение симметричных, антисимметричных и произвольно возбуждаемых колебаний в системе двух идентичных связанных маятников;
ü Измерение частот нормальных колебаний.
Экспериментальная установка
 Рис. 1 Рис. 1 |
ü два идентичных физических маятника (рис.2), представляющих собой массивные стержни 1, длиной 85 см, на которых закреплены грузы 2;
ü нить 3 с дополнительным грузом 4;
ü линейка;
ü секундомер.
Длина стержня – 85 см, масса стержня – 325 г., масса груза – 480 г., масса дополнительного груза – 20 г.
Порядок выполнения работы
Подготовка к эксперименту
1. В тетради, или в программе по обработке электронных таблиц создайте таблицу для записи данных эксперимента и результатов проведённых расчетов. Для этого прочитайте все описание до конца, и решите, какие данные необходимо внести в таблицу. Один из возможных вариантов такой:
| h, см | t+, c | N+, | t‑, с | N‑, | T, с | ω+, c‑1 | ω‑, c‑1 | 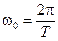 , c‑1 , c‑1 | 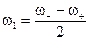 , c‑1 , c‑1 |
При проведении экспериментов заполняются первые 6 столбцов, остальные – при проведении статистической обработки.
2. Установите грузы на одинаковой высоте.
3. Соедините маятники нитью на одинаковых расстояниях h от точек подвеса.
4. Отклоните маятники в одну сторону на одинаковый угол и отпустите их без начального толчка. Измерьте время t+, в течение которого они совершат N+ полных колебаний (N+ =30 ÷ 50). Рассчитайте 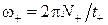 .
.
5. Повторите действия, описанные в п. 4. для антисимметричного нормального колебания. При этом маятники отводятся от положения равновесия в разные стороны на одинаковое расстояние и отпускаются без начального толчка. Измеряется время t-, в течение которого совершаются N- полных колебаний, далее рассчитывается 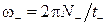 .
.
6. Отклоните один из маятников и понаблюдайте за движением маятников.
7. Измерьте время T между моментами практически полной остановки одного из маятников.
8. Повторите не менее 15 раз действия, описанные в п.п. 4-7 для других значений h.
Обработка и представление результатов
9. Проведите необходимые вычисления и закончите заполнение таблицы.
10. На одном координатном поле постройте графики зависимости частот симметричной и антисимметричной мод от h. Сравните характер этих зависимостей с предсказаниями теории (см. формулы для нормальных частот в литературе [1,2]).
11. На одном координатном поле постройте графики зависимостей w0(h) и w1(h). Сопоставьте оба графика.
Литература
1. Сивухин Д.В. Общий курс физики. Т. I. Механика. - М.: Наука. 1974. -Гл. I.
2. Трубецков Д.И., Рожнёв А.Г. Линейные колебания и волны. - М.: Физматлит. 2001.-Гл. 8.
Упругие волны
Лабораторная работа № 181. Иследование волн на поверхности воды
Введение
Волны на поверхности воды легко наблюдаются. Это позволяет более чётко представить себе ряд основных характеристик и свойств волнового движения.
Приступая к работе необходимо
Знать определения
волны;
амплитуды, частоты, фазы, начальной фазы, периода волны, длины волны, волнового вектора,
фазовой скорости волны.
Знать
вид динамического и кинематического уравнений волны;
выражение для фазовой скорости волн на поверхности воды.
Уметь
измерять расстояния линейкой;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Наблюдение и изучение явлений , характерных для волнового движения, (отражение, преломление, дифракция, интерференция) на примере волн на поверхности воды.
Решаемые задачи
ü Наблюдение плоских и сферических волн, измерение длины волны;
ü Изучение волнового движения вблизи границы раздела двух сред: отражение и преломление волн;
ü Наблюдение интерференции и дифракции;
ü Знакомство с принципом работы стробоскопа
 |
Экспериментальная установка
Приборы и принадлежности:
Волновая кювета (Fig. 1.1)
(1) Рама, 50 см x 36 см x 32 см
(2) Выходная трубка со шланговым зажимом
(3) Кювета с наклоненными боковыми стенками для подавления отраженных волн
(4) Стеклянная пластина, 30 см x 19 см
(5) Направляющая для прикрепления держателей (30) для возбудителей сферических волн (31)
(6) Плексигласовый экран для наблюдения, 50 см x 30 см
(7) Ножка штатива с тремя точками опоры и регулировочным винтом
(8) 2 нивелирующие ножки штатива с тремя точками опоры с регулировочными винтами
(9) 2 стабилизирующие ножки с регулировочными винтами (для стабилизации горизонтального положения, установленного на штативе с тремя точками опоры (7), (8))
(10) Отклоняющее зеркало, 48 см x 33,5 см
Стробоскоп (Fig. 1.1)
(11) Штатив с двумя монтировочными винтами
(12) Стробоскоп с галогенной лампой (12В/55Вт) для освещения волновой кюветы и диска стробоскопа, а также двигателя стробоскопа, провод со специальным разъемом для подключения к разъему DIN (24). Диск стробоскопа можно также вращать вручную.
(13) Световая апертура с конденсорной линзой
(14) Ручка с рифленой головкой для вращения диска стробоскопа вручную, для настройки беспрепятственного испускания света, в случае, когда стробоскоп выключен.
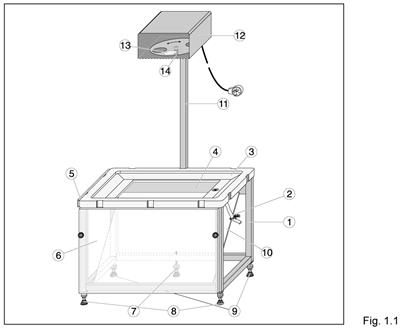
Источник питания (рис. 1.2)
(15) Источник питания; 230 В перем.ток или 115 В перем.ток (согласно техническому паспорту на задней панели прибора), 50/60 Гц, с питающим кабелем.
(16) Сетевой выключатель со световым индикатором
(17) Выключатель стробоскопа
(18) Ручка для точной регулировки частоты стробоскопа (и для соотнесения с частотой возбудителя волн)
(19) Кнопка для генерации одиночных волн
(20) Ручка для регулировки амплитуды возбуждаемых волн
(21) Ручка для регулировки частоты возбуждаемых волн (и частоты стробоскопа)
(22) Воздуховыпускные клапаны для пульсации потока воздуха для возбуждения волн посредством трубки (28)
(23) Разъем для питающего кабеля; держатель для основного и запасного предохранителей. На задней стороне корпуса в техническом паспорте указаны параметры предохранителя.
(24) DIN разъем для кабеля стробоскопа
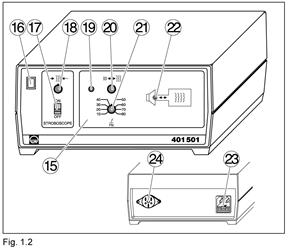
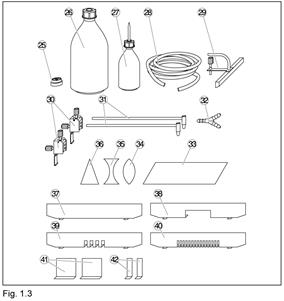
Принадлежности (Рис. 1.3)
(25) Спиртовой уровень для выравнивания горизонтального положения волновой кюветы
(26) Пластиковая бутылка с винтовой крышкой, 1 л
(27) Бутылка для жидкого моющего средства (ПАВ предназначены для снижения поверхностного натяжения)
(28) Трубка для передачи колебаний воздуха
(29) Возбудитель плоских волн, ширина: 19 см
(30) 2 держателя для возбудителей сферических волн, для крепления к направляющей (5)
(31) 2 возбудителя сферических волн
(32) Соединитель с ниппелями, Y-образная форма; для соединения трубки (28) с двумя возбудителями сферических волн
Предметы для экспериментов по преломлению (Рис. 1.3)
(33) Плоскопараллельная пластина из прозрачного акрилового стекла
(34) Двояковыпуклая линза, пластик
(35) Двояковогнутая линза, пластик
(36) Призма, пластик
Препятствия для экспериментов по отражению и интерференции (Рис. 1.3)
(37) Отражающее препятствие
(38) Препятствие с большой щелью, ширина щели: 71 мм
(39) Препятствие с 4 одиночными щелями, ширина щели: 7 мм, расстояние между щелями: 14 мм
(40) Препятствие с 15 одиночными щелями, ширина щели: 4 мм, расстояние между щелями: 8 мм
(41) 2 покровных слайда, ширина: 55 мм
(42) 2 покровных слайда, ширина: 12 мм
Волновая кювета со стробоскопом предназначена для демонстрации образования волн на поверхности воды. С целью генерации волн, колебания мембраны в блоке питания передаются поверхности воды посредством изменения давления воздуха различными возбудителями волн. Частоту возбуждения можно задавать в пределах от 10 Гц до 80 Гц. Кроме того, можно генерировать одиночный волновой импульс.
Для демонстрации образа стоячей волны частоту стробоскопа синхронизируют с частотой генератора колебаний воздуха.
Возбуждение волн
ВНИМАНИЕ: для каждого эксперимента необходимо точно настраивать глубину погружения возбудителя(лей) в воду, частоту и амплитуду колебаний. Часто картину наблюдаемых явлений можно значительно улучшить, изменяя эти параметры. При изменении частоты возбуждения часто приходится менять и амплитуду. Изменение амплитуды позволяет фокусировать различные зоны волновой картины (необходимо учитывать в опытах по дифракции и отражению).
Порядок выполнения работы
Подготовка экспериментальной установки
1. Отгоризонтируйте волновую кювету.
2. Закройте выходную трубку (2) шланговым зажимом. Наполните волновую кювету водой. Уровень воды: для экспериментов по преломлению: 1 мм над предметами в кювете; для всех остальных экспериментов: около 5 мм.
3. Капните каплю жидкого моющего средства для того, чтобы снизить поверхностное натяжение воды и минимизировать возмущающие отражения.
4. Соедините передаточную трубку (28) к воздуховыпускным клапаном (22). Подсоедините кабель стробоскопа (12) к разъему (24). Включите источник питания, нажав сетевой выключатель (16).
  |
5. При необходимости поверните диск стробоскопа так, чтобы луч не прерывался с помощью ручки (14).
6. Пронаблюдайте плоские волны. Для чего сделайте следующее.
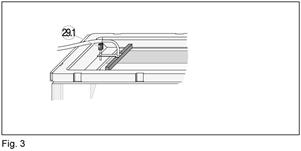
7. Соедините передаточную трубку (28) с переходником возбудителя плоских волн (29) и установите возбудитель в волновой кювете. Установите винт (29.1) таким образом, чтобы нижний край возбудителя слегка касался поверхности воды (см. рис. 3). Если волновые фронты нарушены, капните немного жидкого моющего средства перед возбудителем.
8. Установите желаемую амплитуду и частоту с помощью ручек (20) и (21). При необходимости отрегулируйте возбудитель плоских волн с помощью винта (29.1) или возбудитель круговых волн с помощью винта (30.2) до момента достижения четкого изображения волн.
Замечание: в области низких частот волны можно наблюдать и без стробоскопа. При более высоких частотах возбуждения рекомендуется использование стробоскопа. Он включается с помощью выключателя (17). После небольшого времени разогрева (несколько секунд), на экране появится изображение стоячей волны или медленно движущейся волны. При необходимости поверните ручку (18) для тонкой настройки синхронизации возбудителя и частоты стробоскопа. После выключения стробоскопа, возможно, придется повернуть диск прибора с помощью винта (14), чтобы он не заграждал путь луча.
9. Линейкой измерьте расстояние lп между волновыми поверхностями, отличающимися на 2p.
10. Повторите наблюдения и измерения для 3-4 разных частот.
11. Пронаблюдайте сферические волны. Для чего сделайте следующее.
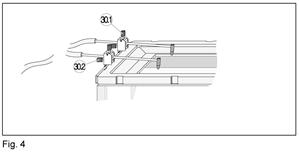
12. Прикрепите держатель (30) к направляющей (5) и закрепите один возбудитель сферических волн (31) с помощью винта (30.1). Затем подсоедините передаточную трубку (28). Установите винт (30.2) таким образом, чтобы нижний край возбудителя слегка касался поверхности воды (см. рис.4).
13. Линейкой измерьте расстояние lп между волновыми поверхностями, отличающимися на 2p.
14. Повторите наблюдения и измерения для 3-4 разных частот.
15. Пронаблюдайте интерференцию сферических волн. Для чего сделайте следующее.
16. Прикрепите держатель (30) к направляющей (5) и закрепите два возбудитель сферических волн (31) с помощью винтов (30.1). Затем подсоедините передаточную трубку (28). Для двойного возбуждения используйте Y-образный соединитель и два коротких кусочка трубки (около 20 см, см. рис. 4). Установите винты (30.2) таким образом, чтобы нижний край возбудителя слегка касался поверхности воды (см. рис.4).
17. Проведите наблюдения для 3-4 частот.
Уборка после эксперимента
18. Слейте воду из кюветы с помощью трубки (2).
19. Осторожно вытрите кювету, особенно стеклянное дно (4) и все остальные части, имеющие контакт с водой. При транспортировке прибора убедитесь, что не жестко установленное зеркало (10) не выпадает.
Обработка и представление результатов
Для плоских и сферических волн рассчитайте длины по формуле l = l/k, где k = 1.65 – коэффициент, обусловленный оптической схемой проекции.
Найдите фазовые скорости поверхностных волн: c = ln. Сделайте вывод о зависимости с(n).
Лабораторная работа № 182. Измерение частоты камертона методом биений
Введение
Биенияявляются частным случаем интерференции волн. Суть явления биений состоит в том, что сумма двух гармонических колебаний близких частот n1 и n2 воспринимается как колебание с частотой n равной (n1+n2)/2 и амплитудой, периодически меняющейся во времени с частотой nБ = |n1-n2|.
Для измерений способом биений необходима некоторая эталонная частота, скажем n1. Колебания этой частоты накладываются на исследуемые колебания. Непосредственно измеряется частота биений, равная разности исследуемой и эталонной частот nБ. Искомая частота
n = n1 ± nБ. (1)
Для выбора одного из знаков необходимы дополнительные соображения, зависящие от конкретного случая.
Приступая к работе необходимо
Знать определения
волны;
амплитуды, частоты, фазы, начальной фазы, периода волны, длины волны, волнового вектора,
фазовой скорости волны;
стоячей волны;
интерференции волн.
Знать
вид динамического и кинематического уравнений волны;
вид гармонического колебания;
Уметь
пользоваться осциллографом;
оценивать случайные погрешности прямых и косвенных измерений.
Цель работы
Освоение способа измерения частоты колебаний с помощью явления биений
Решаемые задачи
ü Знакомство с методом биений звуковых волн;
ü Наблюдение узлов и пучностей стоячих звуковых волн при помощи осциллографа;
ü Измерение частоты биений и частоты камертона при различных положениях муфточки.
Экспериментальная установка
Приборы и принадлежности
ü Осциллограф (4);
ü два камертона (3) (υ0 = 440 Гц) на резонаторных ящиках (2) (на
ü одном - нанесена шкала);
ü муфточки, которые можно укреплять на ветви камертона;
ü секундомер;
ü микрофон (1);
ü молоточек.
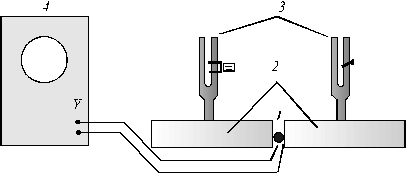 Рис. 4. Рис. 4. |
Микрофон 1 находится в пространстве между резонаторными ящиками 2. Именно там звуковые колебания, создаваемые камертонами 3, имеют максимальную амплитуду. Электрический сигнал с микрофона регистрируется осциллографом 4.
Порядок выполнения работы
1. Снимите муфточку с камертона с делениями. Установите одну из муфточек на другом камертоне ближе к центру ветви. Камертон без муфточки в данном случае является эталонным.
2. Расположите микрофон между резонаторными ящиками, как показано на рисунке выше.
3. Включите питание осциллографа в сеть переменного тока 220 В и дайте прибору прогреться 2-3 минуты: на экране должна появиться светящаяся точка. При помощи ручек управления (яркость, фокус, смещение по «X» и «Y») на панели прибора выведите точку в центр экрана, добейтесь достаточной яркости и резкости.
4. Если ударить молоточком по обоим камертонам, светящая полоска на экране будет периодически изменять свою длину, вследствие звуковых биений. Настройте осциллограф. Для этого, слегка ударяя молоточком по одному из камертонов, переключателем «Volts» на панели осциллографа добейтесь заметного "растяжения" светящейся точки на экране в вертикальном направлении. Теперь можно проводить измерения.
5. Измерьте секундомером время t возможно большего числа n периодов "дыхания" полоски на экране. По формуле nБ = n / t рассчитайте частоту биений.
6. По формуле n1 = n0 - nБ рассчитайте частоту камертона, с закрепленной муфточкой.
7. Повторите измерение n1 несколько раз и найдите среднее значение.
8. Укрепите муфточку напротив самого нижнего деления на камертоне с делениями. Теперь этот камертон будет являться исследуемым, а другой, частота которого n1 уже измерена - эталонным.
9. Последовательно устанавливая муфточку напротив каждого из делений, по описанной методике определите частоты биений и собственные частоты камертона с муфточкой по формуле (1).
Обработка и представление результатов
10. Постройте график зависимости частоты камертона от расстояния муфточки до основания вилки камертона (номера деления, начиная снизу).
11. Объясните наблюдаемые закономерности.
Лабораторная работа № 183. Изучение эффекта Допплера ультразвуковых волн
