Форма отчета по лабораторной работе. Отчет должен содержать: титульный лист; цель работы; условие задачи; текст программы с комментариями; скриншот окна с результатами работы; выводы по

Отчет должен содержать: титульный лист; цель работы; условие задачи; текст программы с комментариями; скриншот окна с результатами работы; выводы по работе.

Вопросы для самоконтроля

1. Назначение функции WinMain.

2. Назначение функции окна.

3. Определение класса окна.

4. Сообщения Windows.

5. Перерисовка окна.

Заключение

В методических указаниях рассмотрены содержание и особенности выполнения лабораторных работ по дисциплине «Алгоритмические языки». Работы выполняются в течение первого семестра со студентами, обучающимися на кафедре ИУ8, и в течение третьего семестра со студентами факультета ГУИМЦ, обучающимися по специальностям кафедры ИУ8.

По каждой лабораторной работе приведены: цель и задачи работы, требования к результатам ее выполнения, краткая характеристика объекта изучения, задачи и порядок выполнения, форма отчета. Также для подготовки студентов представлены вопросы для самоконтроля, в приложении заданы варианты заданий.

Выполнение предложенных работ позволит студенту получить знания, навыки и умения по основным средствам языка Си и подготовится к изучению объектно-ориентированных возможностей языка Си++ на последующих этапах обучения.

Рекомендуемые источники

1. Керниган Б., Ритчи Д. Язык программирования С, 2-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2011. – 304 с.

2. Распространение программного обеспечения по подписке DreamSpark Premium (MSDNAA). [Электронный ресурс] // URL: http://msdnaa.lib.bmstu.ru/default.aspx (дата обращения: 30.06.2015).

3. Подбельский В.В., Фомин С.С. Программирование на языке Си: Учебное пособие. – М.: Финансы и статистика, 2009. – 600 с.

4. Вирт Н. Алгоритмы и структуры данных. Новая версия для Оберона. – М.: ДМК Пресс, 2010. – 272 с.

5. Румянцев П.В. Азбука программирования в Win 32 API. – М.: Горячая Линия - Телеком, 2004. – 312 с.

Приложение А. Варианты заданий для выполнения лабораторных работ

Варианты заданий для лабораторной работы № 1

Часть 1

Вариант № 1

Угол α задан в градусах, минутах и секундах. Найти его величину в радианах (с максимально возможной точностью).

Вариант № 2

Угол α задан в радианах. Найти его величину в градусах, минутах и секундах.

Вариант № 3

Длина отрезка задана в дюймах (1 дюйм=2,54 см). Перевести значение длины в метрическую систему, т.е. выразить ее в метрах, сантиметрах и миллиметрах. Так, например, 21 дюйм = 0 м 53 см 3,4 мм.

Вариант № 4

Заданы моменты начала и конца некоторого промежутка времени в часах, минутах и секундах (в пределах одних суток). Найти продолжительность этого промежутка в тех же единицах измерения.

Вариант № 5

Кубическое уравнение. Заданы три корня кубического уравнения: x1, x2, x3. Найти коэффициенты этого уравнения.

Вариант № 6

Квадратное уравнение. Найти корни квадратного уравнения, заданного своими коэффициентами, с положительным дискриминантом. Подстановкой в уравнение убедиться в погрешности вычислений.

Вариант № 7

Комплексное число. Заданы действительная и мнимая части комплексного числа z=x+ iy. Преобразовать его в тригонометрическую форму и напечатать в виде выражения: z=r(cosφ+i sinφ).

Для справки:

; .

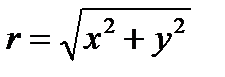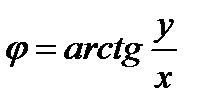Вариант № 8

Движение без топлива? Владелец автомобиля приобрел новый карбюратор, который экономит 50 % топлива, новую систему зажигания, которая экономит 30 % топлива, и поршневые кольца, экономящие 20 % топлива. Верно ли, что его автомобиль теперь сможет обходиться совсем без топлива? Найти фактическую экономию для произвольно заданных сэкономленных процентов.

Вариант № 9

Задача жестянщика. Из круга радиуса r вырезан прямоугольник, большая сторона которого равна a. Найти максимальный радиус круга, который можно вырезать из этого прямоугольника?

Вариант № 10

Приближение sin x. Функция y= sin x на отрезке 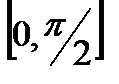хорошо аппроксимируется разложением: 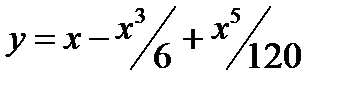. Для заданного значения аргумента x вычислить y по этой формуле и сравнить с точным значением, вычисленным с помощью стандартной функции sin.

Вариант № 11

Переправа. Пловцу надо под прямым углом к фарватеру преодолеть реку шириной b м. Его скорость в стоячей воде 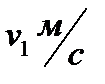; скорость течения реки - 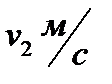. Под каким углом к фарватеру он должен плыть, чтобы его «не снесло»? Сколько времени займет переправа? Как изменится решение, если посередине реки скорость пловца упадет с 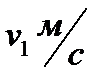до ?

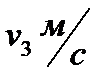Вариант № 12

Вершина параболы. Найти координаты вершины параболы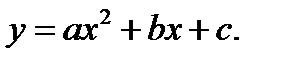

Вариант № 13

Треугольник задается координатами своих вершин на плоскости: 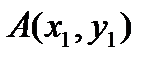, , 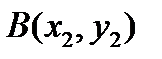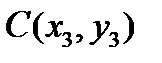. Найти площадь треугольника ABC.

Вариант № 14

Треугольник задается координатами своих вершин на плоскости: 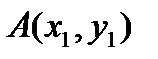, , 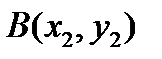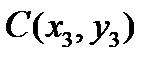. Найти сумму длин медиан треугольника ABC.

Вариант № 15

Треугольник задается координатами своих вершин на плоскости: 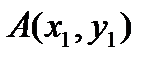, , 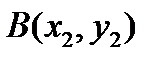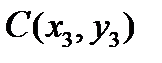. Найти точку пересечения биссектрис треугольника ABC (центр вписанной с него окружности).

Вариант № 16

Треугольник задается координатами своих вершин на плоскости: 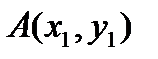, , 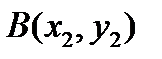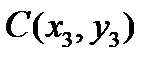. Найти внутренние углы треугольника ABC (в градусах).

Вариант № 17

Треугольник задается координатами своих вершин на плоскости: 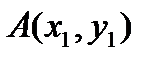, , 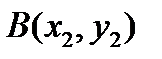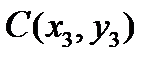. Найти длину и основание высоты, опущенной из вершины A на сторону BC.

Вариант № 18

Треугольник задается координатами своих вершин на плоскости: 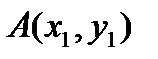, , 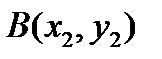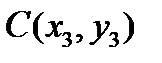. Найти точку D, симметричную точке A относительно стороны BC.

Вариант № 19

В равнобедренном прямоугольном треугольнике известна высота h, опущенная на гипотенузу. Найти стороны треугольника.

Вариант № 20

«Косой» квадрат. У квадрата ABCD на плоскости известны координаты двух противоположных вершин – точек A и C. Найти координаты точек B и D.

Примечание. Расположение квадрата произвольно, его стороны не обязательно параллельны координатным осям.

Вариант № 21

Треугольник ABC задан длинами своих сторон. Найти длину высоты, опущенной из вершины A.

Вариант № 22

Заданы уравнения двух пересекающихся прямых на плоскости: 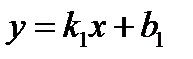, 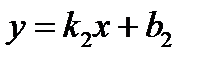. Найти (в градусах, минутах и секундах) угол между ними, используя формулу: .

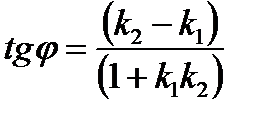Вариант № 23

Трехмерные вектора заданы своими координатами, например, 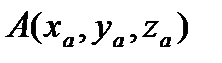, 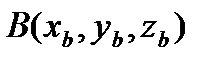. Найти угол в градусах между векторами A и B, используя формулу: .

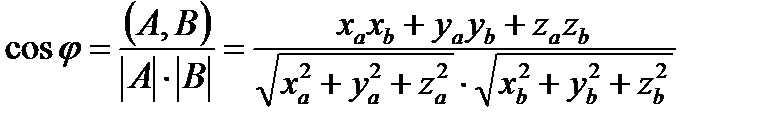Вариант № 24

Трехмерные вектора заданы своими координатами, например, 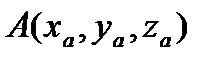, , 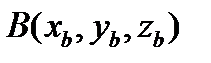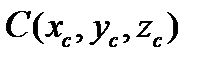. Найти объем пирамиды, построенной на векторах A, B, C, как на сторонах.

Вариант № 25

Трехмерные вектора заданы своими координатами, например, 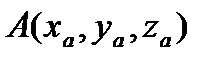, , 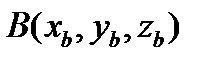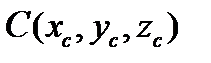. Найти длину диагонали параллелепипеда, построенного на векторах A, B, C, как на сторонах.

Вариант № 26

Определить периметр правильного n-угольника, описанного около окружности радиуса r.

Вариант № 27

Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

Часть 2

Вариант № 1

Даны действительные положительные числа x, y, z. Выяснить, существует ли треугольник с длинами сторон x, y, z.

Вариант № 2

Дано действительное а. Для функции f(a), график которой представлен на рисунке, вычислить f(a).

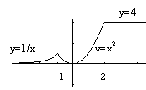
Вариант № 3

Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1, 3). Или вывести сообщение, что таких чисел нет.

Вариант № 4

Даны действительные числа x, y. Если x, y отрицательны, то каждое значение заменить его модулем; если отрицательное только одно из них, то оба значения увеличить на 0.5; если оба значения не отрицательны и ни одно из них не принадлежит отрезку [0.5, 2.0], то оба значения уменьшить в 10 раз; в остальных случаях x, y оставить без изменения.

Вариант № 5

Определить и вывести на печать номер квадранта, в котором расположена точка М(x,y), x и y заданные вещественные числа.

Вариант № 6

Из величин, определяемых выражениями a=sinx, b=cosx, c=ln|x| при заданном х, определить и вывести на экран дисплея минимальное значение.

Вариант № 7

Определить, какая из двух точек - M1(x1, y1) или M2(x2, y2) - расположена ближе к началу координат. Вывести на экран дисплея координаты этой точки.

Вариант № 8

Определить, какая из двух фигур (круг или квадрат) имеет большую площадь. Известно, что сторона квадрата равна а, радиус круга r. Вывести на экран название и значение площади большей фигуры.

Вариант № 9

Определить, попадает ли точка M(x, y) в круг радиусом r с центром в точке (x0, y0)

Вариант № 10

Найти количество положительных (отрицательных) чисел среди четырех целых чисел A, B, C, D.

Вариант № 11

Написать программу, определяющую, есть ли в введенном числе дробная часть. Написать программу, определяющую, есть ли в введенном числе дробная часть.

Вариант № 12

Кирпич. Пройдет ли кирпич со сторонами a, b и c через прямоугольное отверстие со сторонами r и s? Стороны отверстия должны быть параллельны граням кирпича.

Вариант № 13

Шар и ромб. Может ли шар радиуса r пройти через ромбообразное отверстие с диагоналями p и q?

Вариант № 14

Вычислите значение выражения y= sqrt(2Х-1) в случае, когда это возможно (т.е. если (2Х-1)>=0). В противном случае выводите на сообщение «Задайте другое значение Х»

Вариант № 15

Запрашивайте рост и вес пользователя вашей программы. В случае, если вес больше, чем рост -100, то выводите сообщение «Хорошо бы Вам похудеть». В противном случае выводите сообщение «Ваш вес в норме».

Вариант № 16

Если целое число М делится нацело на целое число N, то вывести на экран частное от деления, в противном случае вывести сообщение М на N нацело не делится.

Вариант № 17

Запишите условный оператор, в котором значение переменной с вычисляется по формуле a+b, если а - нечетное и a*b, если а - четное.

Вариант № 18

Написать программу для подсчета суммы только положительных из трех данных чисел.

Вариант № 19

Заданы стороны треугольника: a, b, c. Проверить, является ли этот треугольник остроугольным.

Вариант № 20

Заданы стороны треугольника: a, b, c. Проверить, является ли этот треугольник тупоугольным.

Вариант № 21

Заданы три параметра: a, b, c. Проверить, могут ли эти параметры быть длинами сторон треугольника.

Вариант № 22

Даны три значения. Вывести большее из них.

Вариант № 23

Даны три переменные вещественного типа: A, B, C. Если их значения упорядочены по возрастанию, то удвоить их; в противном случае заменить значение каждой переменной на значение с противоположным знаком. Вывести новые значения переменных A, B, C.

Вариант № 24

Даны вещественные числа a, b, c (a ≠ 0). Выяснить, имеет ли уравнение ах2 + bx + c = 0 вещественные корни.

Вариант № 25

Известны две скорости: одна в километрах в час, другая — в метрах в секунду. Какая из скоростей больше?

Вариант № 26

Даны радиус круга и сторона квадрата, y какой фигуры площадь больше?

Вариант № 27

Даны объемы и массы двух тел из разных материалов. Материал какого из тел имеет большую плотность?

Вариант № 28

Известны сопротивления двух не соединенных друг с другом участков электрической цепи и напряжение на каждом из них. По какому участку протекает меньший ток?

Варианты заданий для лабораторной работы № 2

Вариант № 1

Найти сумму первых k чисел последовательности Фибоначчи. Последовательность определяется законом:

F₀=F₁=1; F_n=F_n-1+F_n-2 - для n³2.

Вариант № 2

Определить первое число последовательности Фибоначчи, превышающее число А. Последовательность определяется законом:

F₀=F₁=1; F_n=F_n-1+F_n-2 - для n³2.

Вариант № 3

Найти все нечетные числа последовательности Фибоначчи, не превышающие заданного числа А. Последовательность определяется законом:

F₀=F₁=1; F_n=F_n-1+F_n-2 - для n³2.

Вариант № 4

Вычислить сумму ряда

¥

S= å (-1)^k-1/k c точностью x=10^-2,…, 10^-6. Точное значение: ln 2.

^K=1

Определить, как изменяется число итераций при изменении точности.

Вариант № 5

Вычислить: .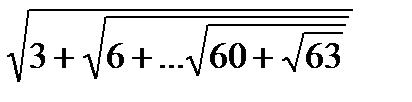

Вариант № 6

Вычислить определенный интеграл методом трапеций:

p/₃

ò (tg²x+ctg²x) dx при n=20, 30, 40 (число шагов разбиения интервала)

p/₆

Вариант № 7

Вычислить сумму ряда

¥

S= 1+å (-1)^k/(2k)! c точностью x=10^-2,…, 10^-6. Точное значение: cos 1.

^K=1

Определить, как изменяется число итераций при изменении точности.

Вариант № 8

Решить задачу, организовав цикл с точностью x=10^-2,…, 10^-6.

Вычислить значение определенного интеграла методом трапеции:

₂

ò e^x(1+sin x)/(1+cos x) dx при x=10^-2,…, 10^-6.

⁰

Вариант № 9

Проверить численно первый замечательный предел 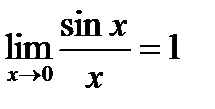, задавая значения x: 1; ½; ¼; 1/8; … до тех пор, пока левая часть равенства не будет отличаться от правой менее чем на заданную погрешность x=10^-2,…, 10^-6, определить как меняется число итераций в зависимости от x.

Вариант № 10

Проверить численно второй замечательный предел 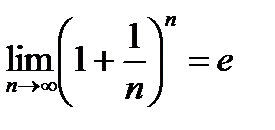, задавая значения n: 1; 2; 3; 4; … При каком n исследуемое выражение отличается от e менее чем на заданную погрешность x=10^-2,…, 10^-6?

Вариант № 11

Сравнить скорость сходимости (число слагаемых для достижения заданной точности x=10^-2,…, 10^-6) следующих разложений числа π:

;

.

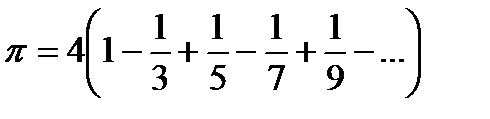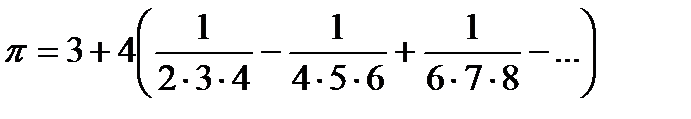Вариант № 12

Сравнить скорость сходимости (число учитываемых элементов для достижения заданной точности x=10^-2,…, 10^-6) при вычислении числа e с помощью ряда и бесконечной дроби:

;

.

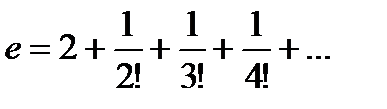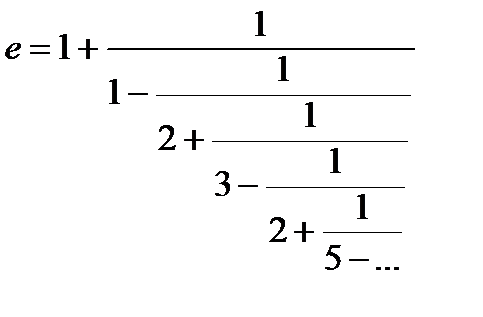Вариант № 13

Сравнить скорость сходимости (число слагаемых для достижения заданной точности x=10^-2,…, 10^-6) следующих разложений числа π:

;

.

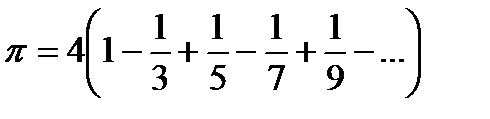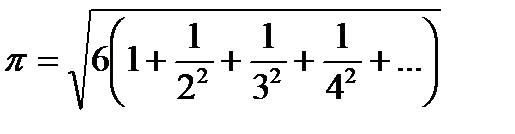Вариант № 14

Для заданных a и p вычислить 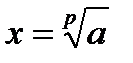по рекуррентному соотношению Ньютона:

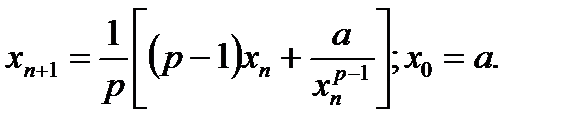
Сколько итераций надо выполнить, чтобы для заданной погрешности x=10^-2,…, 10^-6 выполнялось соотношение: ?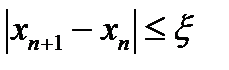

Вариант № 15

Вычислить 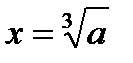для заданного значения a, используя рекуррентное соотношение:

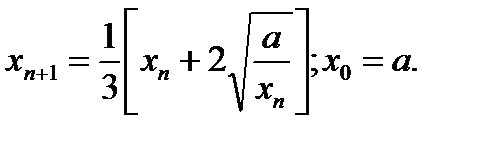
Сколько итераций надо выполнить, чтобы для заданной погрешности x=10^-2,…, 10^-6 выполнялось соотношение: ?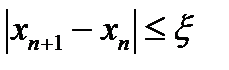

Вариант № 16

Для заданного x>1 вычислить по итерационной формуле 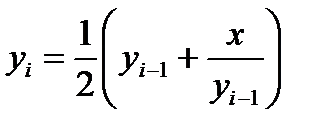с заданной погрешностью x=10^-2,…, 10^-6, задав начальное приближение 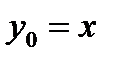. Сравнить с результатом встроенной функции. Сколько итераций пришлось выполнить?

Вариант № 17

Вычислить, организовав цикл с точностью x=10^-2,…, 10^-6. Определить, как меняется число итераций в зависимости от точности.

.

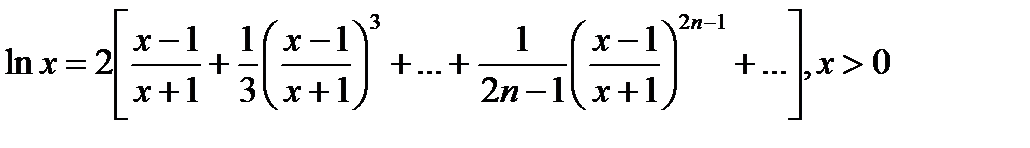Вариант № 18

Вычислить, организовав цикл с точностью x=10^-2,…, 10^-6. Определить, как меняется число итераций в зависимости от точности.

.

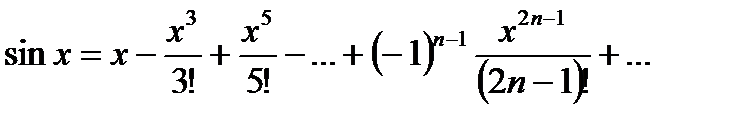Вариант № 19

Вычислить, организовав цикл с точностью x=10^-2,…, 10^-6. Определить, как меняется число итераций в зависимости от точности.

.

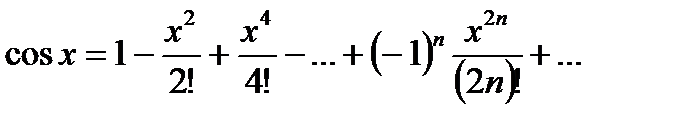Вариант № 20

Вычислить, организовав цикл с точностью x=10^-2,…, 10^-8. Определить, как меняется число итераций в зависимости от точности.

.

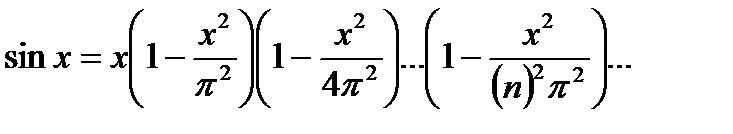Вариант № 21

Вычислить, организовав цикл с точностью x=10^-2,…, 10^-8. Определить, как меняется число итераций в зависимости от точности.

.

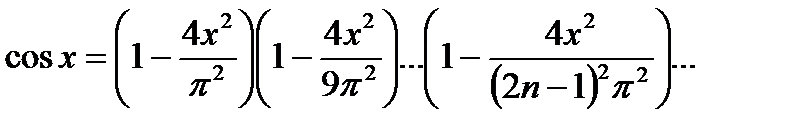Вариант № 22

Вычислить, организовав цикл с точностью x=10^-2,…, 10^-8. Определить, как меняется число итераций в зависимости от точности.

,

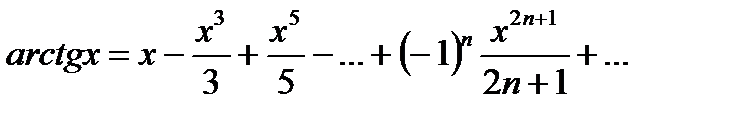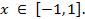
Вариант № 23

Вычислить, организовав цикл с точностью x=10^-2,…, 10^-8. Определить, как меняется число итераций в зависимости от точности.

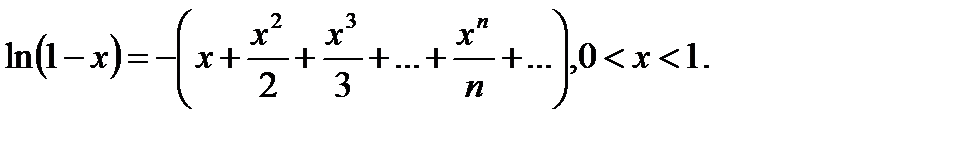
Вариант № 24

Вычислить .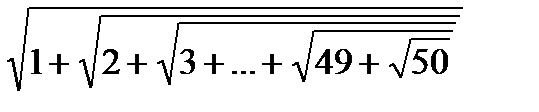

Вариант № 25

Вычислить 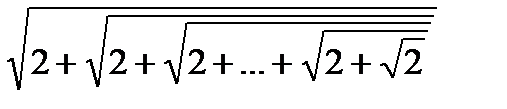; n слагаемых, n вводится с клавиатуры.

Вариант № 26

Вычислить с заданной точностью (x=10^-2,…, 10^-8):

.

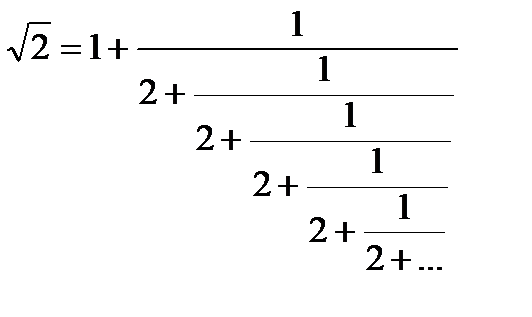Вариант № 27

Вычислить с заданной точностью (x=10^-2,…, 10^-8):

.

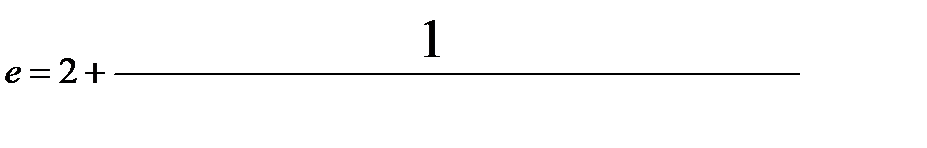Варианты заданий для лабораторной работы № 3

Часть 1. Одномерные массивы

Вариант № 1

Задан одномерный массив целых чисел. Написать программу, которая находит сумму элементов массива.

Вариант № 2

Задан одномерный массив целых чисел. Написать программу, которая находит среднее арифметическое элементов массива.

Вариант № 3

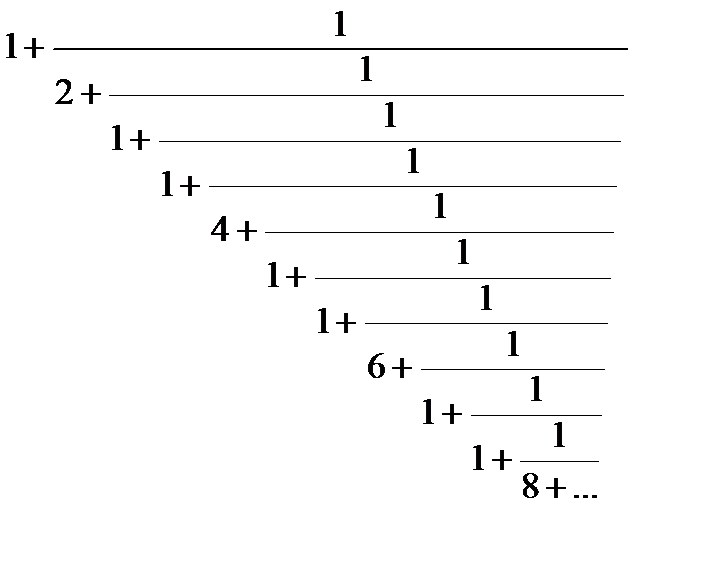
Написать программу, которая находит скалярное произведение двух n-мерных векторов.

Указание. Скалярное произведение определяется по формуле .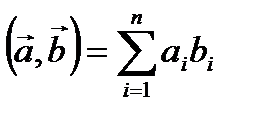

Вариант № 4

Задан одномерный массив целых чисел. Написать программу, которая "переворачивает" массив, т. е. меняет местами его первый и последний элементы, второй и предпоследний и т. д.

Вариант № 5

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит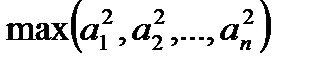

Вариант № 6

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит .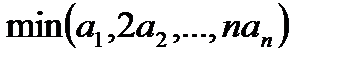

Вариант № 7

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит .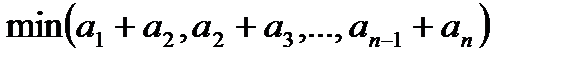

Вариант № 8

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит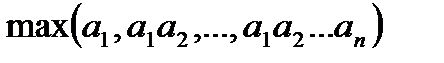

Вариант № 9

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит количество четных чисел среди чисел a₁, a₂,…, a_n.

Вариант № 10

Задан одномерный массив целых чисел. Написать программу, которая выводит элементы массива на экран и находит произведение элементов массива.

Вариант № 11

Задан одномерный массив целых чисел. Написать программу, которая выводит элементы массива на экран и находит среднее геометрическое элементов массива.

Вариант № 12

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит сумму четных чисел среди чисел a₁, a₂,…, a_n.

Вариант № 13

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит сумму элементов с четными индексами.

Вариант № 14

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит сумму элементов с четными индексами.

Вариант № 15

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая меняет местами минимальный и максимальный элементы (или любую пару из этих элементов в случае, если таких элементов несколько).

Вариант № 16

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит индекс минимального элемента.

Вариант № 17

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит минимальный элемент среди элементов с четными индексами.

Вариант № 18

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит максимальный четный элемент.

Вариант № 19

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит сумму отрицательных элементов (при формировании массива обеспечить, чтобы были отрицательные элементы).

Вариант № 20

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая считает число нечетных элементов.

Вариант № 21

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая считает число элементов кратных 3.

Вариант № 22

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая считает сумму элементов кратных 7.

Вариант № 23

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая выводит индексы отрицательных элементов на экран (при формировании массива обеспечить, чтобы были отрицательные элементы).

Вариант № 24

Заданы целые числа a₁, a₂,…, a_n. Число b вводится с клавиатуры, проверить, есть ли в массиве элемент со значением b. Если элемент есть, то вывести индекс (индексы) такого элемента.

Вариант № 25

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая находит количество положительных элементов (при формировании массива обеспечить, чтобы были отрицательные элементы).

Вариант № 26

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая отрицательные элементы заменяет на их абсолютные значения и печатает преобразованный массив (при формировании массива обеспечить, чтобы были отрицательные элементы).

Вариант № 27

Заданы целые числа a₁, a₂,…, a_n. Написать программу, которая нечетные элементы удваивает и печатает преобразованный массив.

Часть 2. Многомерные массивы (матрицы)

Вариант № 1

Заданы матрица с элементами размерности n×m и вектор с элементами размерности m. Написать программу, которая находит произведение матрицы на вектор.

Указание. Результатом перемножения матрицы на вектор является вектор размерности n с компонентами .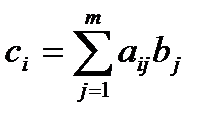

Вариант № 2

Заданы две матрицы: размерности n×m и размерности m×l. Написать программу, которая находит произведение этих матриц.

Указание. Результатом перемножения двух матриц является матрица размерности n×l с элементами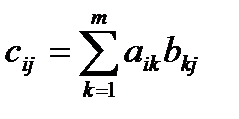

Вариант № 3

Задана квадратная матрица размерности n×n. Написать программу, которая находит транспонированную матрицу.

Указание. Транспонированием матрицы называется преобразование, при котором элементы и меняются местами. При транспонировании строки становятся столбцами, а столбцы − строками.

Вариант № 4

Задана действительная матрица a_ij размерности n×m. Написать программу, которая определяет числа b₁, b₂, …, b_n, равные суммам элементов строк матрицы.

Вариант № 5

Задана целочисленная матрица a_ij размерности n×m. Написать программу, которая определяет числа b₁, b₂, …, b_n, равные произведениям элементов строк матрицы.

Вариант № 6

Задана действительная матрица a_ij размерности n×m. Написать программу, которая определяет числа b₁, b₂, …, b_n, равные наименьшим значениям элементов строк матрицы.

Вариант № 7

Задана целочисленная матрица a_ij размерности n×m. Написать программу, которая определяет действительные числа b₁, b₂, …, b_n, равные значениям средних арифметических элементов строк матрицы.

Вариант № 8

Задана действительная матрица a_ij размерности n×m. Написать программу, которая определяет числа b₁, b₂, …, b_n, показывающие, сколько отрицательных элементов расположено в каждой строке матрицы.

Вариант № 9

Задана квадратная целочисленная матрица a_ij размерности n×n. Написать программу, которая заменяет все отрицательные элементы матрицы на −1, положительные − на 1, а нулевые элементы оставляет без изменения.

Вариант № 10

Задана действительная матрица a_ij размерности n×m. Написать программу, которая вычисляет новую матрицу b_ij. Матрица получается путем деления всех элементов заданной матрицы a_ij на ее наибольший по модулю элемент.

Вариант № 11

Задана целочисленная матрица a_ij размерности n×m. Написать программу, которая определяет числа b₁, b₂, …, b_n, равные числу нечетных элементов в строках матрицы.

Вариант № 12

Задана действительная матрица a_ij размерности n×m. Написать программу, которая определяет действительные числа b₁, b₂, …, b_n, равные значениям средних геометрических элементов строк матрицы.

Вариант № 13

Задана действительная матрица a_ij размерности n×m. Написать программу, которая определяет действительные числа b₁, b₂, …, b_n, равные значениям минимальных элементов строк матрицы.

Вариант № 14

Задана действительная матрица a_ij размерности n×m. Написать программу, которая определяет целые числа b₁, b₂, …, b_n, равные индексам максимальных элементов строк матрицы (если в строке 2 и более максимальных элементов, то использовать любой индекс).

Вариант № 15

Задана действительная матрица a_ij размерности n×m. Написать программу, которая определяет целые числа b₁, b₂, …, b_n, равные числу отрицательных элементов строк матрицы (при формировании матрицы обеспечить наличие в ней отрицательных элементов).

Вариант № 16

Улитка. Матрицу M(m, n) заполнить натуральными числами от 1 до m x n по спирали, начинающейся в левом верхнем углу и закрученной по часовой стрелке.

Вариант № 17

Работа комбайнера. Матрицу K(m, n) заполнить следующим образом. Элементам, находящимся на периферии (по периметру матрицы), присвоить значение 1; периметру оставшейся подматрицы - значение 2 и так далее до заполнения всей матрицы.

Вариант № 18

Символьную матрицу A(m, n) заполнить символами с кодами менее 128. Найти строки, содержащие только цифры от 0 до 9, или вывести сообщение, что таких строк нет.

Вариант № 19

Матрицу A(m, n) заполнить следующим образом. Для заданных k и l (k и l вводятся с клавиатуры) элементу a_kl присвоить значение 1; элементам, окаймляющим его (соседним с ним по вертикали, горизонтали и диагоналям) - значение 2; элементам следующего окаймления - значение 3 и так далее до заполнения всей матрицы.

Вариант № 20

Матрица K(m, m) состоит из нулей и единиц. Найти в ней номера (индексы) хотя бы одной строки или хотя бы одного столбца, не содержащих единицы, либо сообщить, что таковых нет.

Вариант № 21

Латинский квадрат. Латинским квадратом порядка n называется квадратная таблица размером, каждая строка и каждый столбец которой содержат все числа от 1 до n. Проверить, является ли заданная целочисленная матрица латинским квадратом.

Вариант № 22

Магический квадрат. Магическим квадратом порядка n называется квадратная таблица размером n, состоящая из чисел так, что суммы по каждому столбцу, каждой строке и каждой из двух диагоналей равны между собой. Проверить, является ли заданная целочисленная квадратная матрица магическим квадратом.

Вариант № 23

Развитие задачи магический квадрат. Реализовать любой алгоритм построения магического квадрата заданного размера n.

Вариант № 24

Крестики-нолики. Клеточное поле размером есть результат игры в крестики-нолики на "бесконечном" поле (задать размерность поле равное n). Проверить, не закончена ли игра выигрышем "крестиков"? Считается, что "крестики" выиграли, если на поле найдется по горизонтали, вертикали или диагонали цепочка, состоящая подряд из 5 крестиков.

Вариант № 25

В каждой строке матрицы A(n, n) найти наибольший элемент и поменять его местами с соответствующим диагональным элементом.

Вариант № 26

Матрица L(n, k) состоит из нулей и единиц. Найти в ней самую длинную цепочку подряд стоящих нулей по горизонтали, вертикали или диагонали.

Вариант № 27

Символьную матрицу A(m, n) заполнить символами с кодами менее 128. Найти строки, содержащие только английские буквы, или вывести сообщение, что таких строк нет.

Варианты заданий для лабораторной работы № 4

Варианты 1- 12

Определить структуру «студент», поля структуры: ФИО, массив элементов структуры «дисциплина» (не менее 4-х элементов, результаты сдачи сессии), при необходимости можно использовать дополнительные поля (например, число элементов в массиве дисциплин). Структура «дисциплина» включает поля: название, оценка. Определите недостаток подобного представления данных, если описываются результаты сдачи сессии одной группой, и предложите способы его устранения.

В программе задайте группу студентов (массив переменных структурного типа) и выполните следующие действия.

1) Определите, сколько студентов имеют неудовлетворительную оценку хотя бы по одному предмету.

2) Определите, сколько студентов сдали все экзамены на 5.

3) Определите средний балл группы по заданной дисциплине.

4) Определите количество отличных оценок, полученных группой по всем предметам.

5) Определите, сколько студентов имеют неудовлетворительную оценку по заданному предмету.

6) Определите, сколько студентов имеют средний балл от 4 до 5.

7) Определите, какое количество неудовлетворительных оценок получено по всем предметам.

8) Определите, какой из предметов был сдан группой лучше всего.

9) Определите, сколько студентов не имеют задолженностей.

10) Определите, сколько студентов сдали сессию на 4 и 5.

11) Определите студентов с самым высоким средним баллом (один студент или несколько с одинаковыми баллами).

12) Определите средний балл каждого студента.

Варианты 13- 20

Определите структуру «Житель». Поля: ФИО, переменная структурного типа «адрес» (поля: улица, номер дома, номер квартиры), пол, возраст.

В программе задайте несколько жителей – фрагмент базы данных ЖЭК (массив переменных структурного типа) и выполнить следующие действия.

13) Определите, сколько лиц женского и сколько мужского пола проживают в заданном доме.

14) Определите, сколько лиц мужского пола в возрасте старше 18 лет и младше 60 проживают на одной улице.

15) Определите, сколько лиц женского пола в возрасте старше 30 лет проживают в заданном доме.

16) Определите, сколько детей до 7 лет проживают на одной улице.

17) Определите, сколько лиц мужского пола и женского в возрасте до 50 лет проживают на заданной улице.

18) Определите, сколько детей от 1 года до 5 проживают в заданном доме.

19) Определите, сколько лиц мужского пола призывного возраста (от 18 до 27 лет) находится в базе данных.

20) Определите, число пенсионеров (мужчины с 60 лет, женщины с 55) находится в базе данных.

Варианты 21- 27

Определите структуру «Пассажир» и поместите в нее следующую информацию: ФИО пассажира, массив элементов структуры «багаж» (поля: название предмета багажа, вес предмета в кг), при необходимости можно использовать дополнительные поля (например, число элементов в массиве багажа). В программе задайте несколько пассажиров (массив переменных структурного типа) и выполните следующие действия.

21) Определите число пассажиров, вес багажа которых превышает 30 кг.

22) Определите, имеется ли пассажир, багаж которого состоит из одной вещи весом более чем в 20 кг.

23) Определите средний вес багажа для пассажира.

24) Определите количество пассажиров, вес багажа которых превосходит средний.

25) Определите количество пассажиров, имеющих более трех вещей в багаже.

26) Определите средний вес одного предмета багажа для каждого пассажира.

27) Определите пассажира с максимальным весом багажа.

Варианты заданий для лабораторной работы № 5

Вариант № 1

Решить задачу, используя функцию.

Дано четное число N>2. Проверить для него гипотезу Гольдбаха, состоящую в том, что каждое четное число представимо в виде суммы двух простых чисел. Функция должна проверять является целое число простым или нет (простым является число, если оно делится без остатка только на себя и на 1).

Вариант № 2

Решить задачу, используя функцию.

Дана целочисленная матрица размера N*M. Преобразовать ее, переставив строки в порядке возрастания их наименьших элементов. Функция должна возвращать значение наименьшего элемента в одномерном массиве.

Вариант № 3

Решить задачу, используя функцию.

Дана матрица размера N*M. Преобразовать ее, упорядочив каждую строку по неубыванию элементов. Функция должна сортировать одномерный массив в порядке неубывания его элементов.

Вариант № 4

Решить задачу, используя функцию.

Дана квадратная целочисленная матрица А порядка n. Выделяя на главной диагонали последовательно по одному элементу A_ii, можно получить n матриц, ограниченных элементами A₁₁ и А_ii. Программа должна сформировать вектор, элементами которого являются наибольшие элементы всех таких матриц. Функция должна возвращать значение наибольшего элемента в матрице размерности n.

Вариант № 5

Решить задачу, используя функцию.

Определить количество простых чисел в целочисленном массиве С(n). Функция должна проверять является целое число простым или нет (простым является число, если оно делится без остатка только на себя и на 1).

Вариант № 6

Решить задачу, используя функцию.

Дана вещественная матрица A(n,m). Упорядочить матрицу по невозрастанию сумм элементов ее строк. Функция должна возвращать значение суммы элементов одномерного массива.

Вариант № 7

Решить задачу, используя функцию.

Дана символьная матрица размера n*m. Преобразовать ее таким образом, чтобы элементы каждой нечетной строки расположились в обратном порядке. Новую матрицу не заводить. Функция должна переписывать одномерный символьный массив в обратном порядке.

Вариант № 8

Решить задачу, используя функцию.

Даны три матрицы разных порядков (n1*m1, n2*m2, n2*m3). Найти сумму их наименьших элементов (считая, что в каждой матрице такой элемент единственный). Функция должна возвращать значение наименьшего элемента матрицы размерности n*m.

Вариант№ 9

Решить задачу, используя функцию.

Дан массив из n натуральных чисел. Определить количество чисел, в десятичной записи которых используется цифра 7. Функция должна проверять, если в десятичной записи целого числа цифра 7 или нет.

Вариант№ 10

Решить задачу, используя функцию.

Найдите наибольший общий делитель (НОД) 3-х натуральных чисел, используя соотношение НОД(a, b, c)=НОД(НОД(a, b), c). Функция должна находить НОД 2- х чисел по алгоритму Евклида.

Алгоритм Евклида:

1. Вычислим r - остаток от деления числа a на b (a>b), a = bq+r, 0 <= r < b.

2. Если r = 0, то b есть искомое число (НОД).

3. Если r != 0, то заменим пару чисел (a,b) парой (b,r), и перейдем к шагу 1.

Вариант№ 11

Решить задачу, используя функцию.

Дана матрица А(n,m). Определить суммы элементов тех строк матрицы, максимальные элементы которых не превышают среднего значения элементов матрицы или вывести сообщение, что таких строк не существует. Функция должны вычислять или значение суммы элементов одномерного массива или значение максимального элемента одномерного элемента или среднее значение элементов матрицы (можно использовать сразу три функции).

Вариант № 12

Решить задачу, используя функцию.

Для заданного m получить таблицу первых m простых чисел. Функция должна проверять является целое число простым или нет (простым является число, если оно делится без остатка только на себя и на 1).

Вариант № 13

Решить задачу, используя функцию.

Дан массив из n натуральных чисел. Определить количество чисел, десятичная запись которых не содержит одинаковых цифр. Функция должна проверять, содержит десятичная запись числа одинаковые цифры или нет.

Вариант № 14

Решить задачу, используя функцию.

В вещественном массиве размерности n найти все числа, у которых старшая значащая десятичная цифра есть 9 (числа сильно различаются по величине). Функция должна проверять для вещественного числа является старшая значащая десятичная цифра 9 или нет.

Вариант № 15

Решить задачу, используя функцию.

Дан массив натуральных чисел размерности n. Для каждого числа переставьте его десятичные числа так, чтобы получить максимально возможное число, записанное теми же цифрами. Функция должна переставлять цифры одного натурального числа, возвращаемое значение не использовать (тип void). Примечание: достаточно цифры числа отсортировать по невозрастанию.

Вариант № 16

Решить задачу, используя функцию.

Дан массив натуральных чисел размерности n. Определить число чисел палиндромов в нем. Палиндром («перевертыш») – число, десятичная запись которого читается одинаково слева направо и справа налево (например, 14541). Функция должна проверять является число палиндромом или нет.

Вариант № 17

Решить задачу, используя функцию.

Получить все шестизначные «счастливые» номера и подсчитать их количество. Функция должна проверять является число «счастливым» или нет. «Счастливым» называется такое шестизначное число, у которого сумма первых трех цифр равна сумме последних трех.

Вариант № 18

Решить задачу, используя функцию.

Дан массив натуральных чисел размерности n. Отсортировать массив в порядке неубывания сумм цифр десятичной записи чисел. Функция должна считать сумму десятичных цифр натурального числа.

Вариант № 19

Решить задачу, используя функцию.

Дата некоторого дня характеризуется тремя натуральными числами (число, месяц, год). Определите количество дней, прошедших между двумя датами (учитывать високосные годы, даты начинаются с 1970 года). Функция должна считать, сколько дней прошло с 1 января 1970 года до текущей даты.

Вариант № 20

Решить задачу, используя функцию.

Дан массив натуральных чисел размерности n. Отсортировать его в порядке неубывания числа единиц в двоичной записи чисел. Функция должна считать число единиц в двоичной записи числа.

Вариант № 21

Решить задачу, используя функцию.

Дан массив натуральных чисел размерности n. Вывести на печать все числа этого массива, являющиеся полными квадратами. Функция должна проверять, является число полным квадратом или нет.

Вариант № 22

Решить задачу, используя функцию.

Дан массив натуральных чисел размерности n. Вывести на печать все числа этого массива, являющиеся степенями пятерки. Функция должна проверять, является число степенью пятерки или нет.

Вариант № 23

Решить задачу, используя функцию.

Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Напечатать все пары «близнецов», не превышающих заданного значения a. Функция должна проверять является целое число простым или нет (простым является число, если оно делится без остатка только на себя и на 1).

Вариант № 24

Решить задачу, используя функцию.

Дан массив натуральных чисел размерности n. Найти число в массиве, имеющее максимальную сумму цифр в десятичном представлении, если существует несколько чисел с одинаковой максимальной суммой, то вывести на печать их все. Функция должна возвращать сумму цифр числа в десятичном представлении.

Вариант № 25

Решить задачу, используя функцию.

Даны два натуральных числа a и b – числитель и знаменатель дроби. Сократите дробь, разделив числа на их наибольший общий делитель (НОД). Функция должна находить НОД 2- х чисел по алгоритму Евклида.

Алгоритм Евклида:

1. Вычислим r - остаток от деления числа a на b (a>b), a = bq+r, 0 <= r < b.

2. Если r = 0, то b есть искомое число (НОД).

3. Если r != 0, то заменим пару чисел (a,b) парой (b,r), и перейдем к шагу 1.

Вариант № 26

Решить задачу, используя функцию.

Составить программу для нахождения общего числа некоторой буквы (буква вводится с клавиатуры) в нескольких предложениях (предложение задается строкой в языке Си). Функция считает количество заданной буквы в строке.

Вариант № 27

Решить задачу, используя функцию.

Даны три квадратных уравнения: 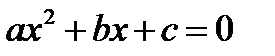, , 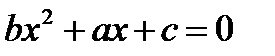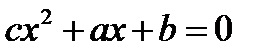. Сколько из них имеют вещественные корни. Функция должна проверять имеет квадратное уравнение вещественные корни или нет.

Варианты заданий для лабораторной работы № 6

В приложении организовать список объектов и сортировку списка. Варианты заданий заданы в ячейках таблицы А.1. Параметры приложений указаны в заголовках строк и столбцов таблицы А.1.

Таблица А.1 – Варианты заданий

Параметры приложений	Метод сортировки
Метод вставки	Метод прямого выбора	Метод обмена («пузырька»)
Объект- сотрудник (поля: ФИО, дата приема на работу, должность, базовый оклад)	Сортировка по ФИО
Сортировка по окладу
Объект- банковский вклад (поля: название, сумма вклада, тип валюты, ставка в % годовых)	Сортировка по сумме вклада
Сортировка по названию
Объект- студент (поля: ФИО, группа, номер зачетной книжки, массив 4-х оценок за сессию)	Сортировка по ФИО
Сортировка по среднему баллу
Объект- книга (поля: ФИО автора, название, издательство, год издания, число страниц)	Сортировка по ФИО
Сортировка по названию
Объект- автомобиль (поля: название модели, массив расходов топлива из 3-х элементов (на трассе, в городе, смешанный), максимальная скорость, мощность)	Сортировка по названию модели
Сортировка по смешанному расходу топлива

Варианты заданий для лабораторной работы № 7

Варианты заданий заданы в ячейках таблицы А.2. Параметры приложений указаны в заголовках строк и столбцов таблицы А.2.

Таблица А.2 – Варианты заданий

Параметры приложений	Файл открывается в текстовом режиме	Файл открывается в двоичном режиме
Структура студент (поля: ФИО, группа, номер зачетной книжки, массив 4-х оценок за сессию)	Объекты в первом приложении задаются списком, во втором – массивом
Объекты в первом приложении задаются массивом, во втором – списком
Структура книга (поля: ФИО автора, название, издательство, год издания, число страниц)	Объекты в первом приложении задаются массивом, во втором – списком
Объекты в первом приложении задаются списком, во втором – массивом
Структура автомобиль (поля: модель, массив расходов топлива из 3-х элементов (на трассе, в городе, смешанный), максимальная скорость, мощность)	Объекты в первом приложении задаются списком, во втором – массивом
Объекты в первом приложении задаются массивом, во втором – списком
Структура сотрудник (поля: ФИО, дата приема на работу, должность, базовый оклад)	Объекты в первом приложении задаются массивом, во втором – списком
Объекты в первом приложении задаются списком, во втором – массивом
Структура банковский вклад (поля: Продолжение таблицы А.2 название, сумма вклада, тип валюты, ставка в % годовых)	Объекты в первом приложении задаются списком, во втором – массивом
Объекты в первом приложении задаются массивом, во втором – списком
Структура компьютер (поля: тип процессора, тактовая частота, объем оперативной памяти, размер жесткого диска, тип видеокарты)	Объекты в первом приложении задаются массивом, во втором – списком
Объекты в первом приложении задаются списком, во втором – массивом
Структура программное средство криптозащиты (поля: название разработчика, номер версии, название реализуемого алгоритма, наличие лицензии ФСБ- да, нет)	Объекты в первом приложении задаются списком, во втором – массивом
Объекты в первом приложении задаются массивом, во втором – списком

Варианты заданий для лабораторной работы № 8

Разработать приложение для рисования в окне с помощью мыши (функции простого графического редактора).

Варианты заданий заданы в ячейках таблицы А.3. Параметры приложений указаны в заголовках строк и столбцов таблицы А.3.

Таблица А.3 – Варианты заданий

Параметры приложений	Параметры границы и закраски фигур
Рисуемый элемент	Клавиша «мыши» для рисования	Граница пунктирная синего цвета, закраска красными вертикальными линиями	Граница точечная зеленого цвета, закраска желтыми горизонтальными линиями	Граница «точка- тире» красного цвета, закраска синими горизонтальными и вертикальными линиями	Граница «две точки- тире» фиолетового цвета, закраска желтыми наклонными диагональными слева- направо и справа- налево линиями
Небольшие круги (50х50 пикселей) по следу курсора при перемещении «мыши» с нажатой клавишей	Левая
Правая
Прямоугольники, начальный угол- точка положения курсора мыши в момент нажатия клавиши, рисование происходит при перемещении мыши с нажатой клавишей, конечный угол прямоугольника- положение курсора в момент отпускания клавиши	Левая
Правая
Овалы, вписанные в прямоугольники (прямоугольники рисовать не надо), начальный угол- точка положения курсора мыши в момент нажатия клавиши, рисование происходит при перемещении мыши с нажатой клавишей, конечный угол прямоугольника- положение курсора в момент отпускания клавиши	Левая
Правая
Отрезки, начальная точка – точка положения курсора мыши в момент нажатия клавиши, рисование происходит при перемещении мыши с нажатой клавишей, конечная точка- положение курсора в момент отпускания клавиши	Левая
Правая