Древовидные и табличные структуры

Под системой мы понимаем единство взаимосвязанных предметов и явлений в природе и обществе. Поэтому система характеризуется как своим составом, так и своей структурой, т.е. взаимосвязями ее элементов и их соподчиненностью (иерархией). Иерархия означает, что элементы каждой системы связаны друг с другом и что среди них находятся главные (определяющие, ведущие) и соподчиненные им (определяемые, ведомые ими) элементы. Структурирование системы заключается в установлении иерархии между элементами системы и их взаимосвязей. Общих правил определения в системе главных элементов и их взаимосвязей не существует. Структуру системы можно описать различными способами.

Часто используется иерархическая структура типа "дерево". Применение этой структуры возможно, когда все подсистемы строго соподчинены своим надсистемам.

Рассмотрим для примера структуру некоего института. Для простоты предположим, что в институте всего три факультета: физический, химический и биологический. На физическом факультете три кафедры: общей, теоретической и экспериментальной физики. На химическом факультете всего две кафедры: кафедра органической и неорганической химии. А на биологическом факультете есть кафедры ботаники, зоологии и анатомии.

Системы в дереве разделены на уровни. На первом уровне находится самая сложная система, которая называется корнем дерева. На втором уровне – три ее подсистемы (три ветви), которые подчинены всей системе. В свою очередь, каждая система второго уровня разбита на соответственно подчиненные им подсистемы. Системы самого нижнего уровня называют листьями. По линиям связи дерева легко определить, какая кафедра какому факультету принадлежит. Аналогично отражена принадлежность факультетов институту.

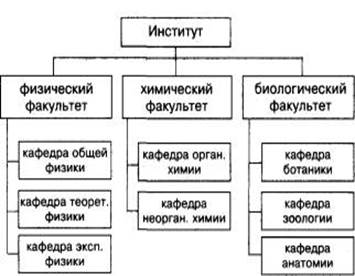
Структура типа "дерево"

В дереве соотношения между верхними и нижними уровнями имеют характер "один ко многим". Для наглядности структуру системы можно изобразить геометрически. Для этого ее элементы изображают чаще всего плоскими геометрическими фигурами. При этом главные элементы можно изображать в верхней части схемы, а соподчиненные – под ними. Связи между элементами изображают стрелками или отрезками.

Методы поиска в массиве

Методы поиска в массиве: последовательный, бинарный, интерполяционный, фибоначчи и др. Для поиска в массиве предполагается, что ключи упорядочены: 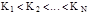. Исход поиска удачен, если ключ найден, и неудачен, если ключ не найден.

Последовательный метод заключается в последовательном переборе всех ключей до тех пор, пока один из них не совпадет с искомым ключом. Это не самый быстрый метод.

Бинарный метод - сначала сравниваем К с ключом среднего элемента. Результат сравнения позволит определить, в какой половине таблицы продолжать поиск. К этой половине снова применяем ту же процедуру и т.д. Алгоритм бинарного метода (l, u - указатели верхней и нижней границ поиска):

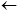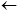А1.[Начальная установка] Установить l 1, u N.

A2.[Поиск середины] Если u<l, то алгоритм заканчивается неудачно. Иначе установить i 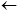[(l+u)/2].

A3.[Сравнение] Если K<K_i, то перейти на А4, если К>K_i, то - на А5, если К=K_i, то алгоритм заканчивается успешно.

А4.[Корректировка u] Установить u 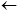i-1 и вернуться к шагу А2.

А5.[Корректировка l] Установить l 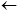i+1 и вернуться к шагу А2.

За более чем 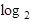N сравнений ключ будет либо найден, либо будет установлено его отсутствие.

Вместо трех указателей - l,u,i можно использовать два - текущее положение i и величину смещения. Такая модификация называется однородным бинарным поиском. Алгоритм такой:

B1. [Начальная установка] Установить i 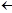[N/2], m 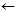{N/2}.

B2. [Сравнение] Если К< К_i то перейти на В3. если К>K_i, то - на В4, если К=K_i, то алгоритм заканчивается успешно.

В3. [Уменьшение i] Если m=0, то алгоритм заканчивается неудачно. Иначе установить i 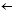i-[m/2], m 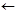{m/2} и вернуться на В2.

В4. [Увеличение i] Если m=0, то алгоритм заканчивается неудачно. Иначе установить i 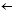i+[m/2], m 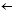{m/2} и вернуться на В2.

([x] - целая часть х, {x} - наименьшее целое число, большее х)

Интерполяционный метод заключается в том, чтобы отступать от текущего ключа (несовпадающего с искомым) на расстояние, зависящее от разницы между текущим и искомым ключами - отступают на расстояние 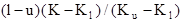от l. Метод за не более чем 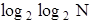сравнений позволяет либо найти, либо установить отсутствие этого ключа. Этот метод наиболее эффективен для ключей, возрастающих, как арифм. прогрессия, и для очень больших N, когда 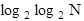будет существенно меньше 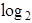N.