Деревья вывода. Канонические выводы. Двусмысленные порождающие грамматики.
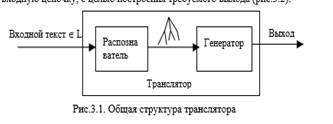
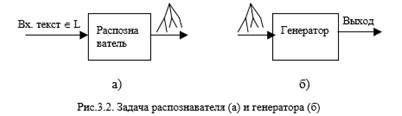
Основная идея Хомского состоит в том, что понимание цепочки языка должно основываться на структуре этой цепочки. В данной главе на примерах показывается, каким образом структура цепочки – дерево ее вывода в порождающей контекстно-свбодной грамматике, может быть использовано для генерации требуемого выхода транслятора. 3.1. Дерево вывода как основа семантических вычислений Рис.3.1 повторяет представленную в главе 1 общую структуру транслятора. После рассмотрения понятий грамматики, синтаксического анализа и дерева вывода эта структура приобретает бόльшую определенность: задачей распознавателя является восстановление дерева вывода входной цепочки в заданной КС-грамматике, а задачей генератора – использование дерева вывода для вычисление смысла, вложенного в эту входную цепочку, с целью построения требуемого выхода (рис.3.2).
Задачей транслятора является генерация нужного выхода для каждой входной цепочки языка. Поэтому предварительный синтаксический анализ (рис.3.2 а) представляется вспомогательной, дополнительной задачей. Для того, чтобы выявить важность этого этапа, мы сначала рассмотрим, как построение дерева вывода может быть использовано для решения основной задачи трансляции. Будем считать, что дерево вывода цепочки уже построено распознавателем с помощью некоторого алгоритма синтаксического анализа (рис.3.2 б).
Множество смыслов, которые можно приписать символам, фразам и предложениям языка – это в общем случае некоторое множество элементов любой природы. Не существует правил, позволяющих определить смысл слова по его звучанию, смысл символа, знака по его изображению. Связь звучания слова, начертания символа с их смыслом должна быть заучена (задана некоторой конечной функцией). Словарь любого языка конечен, и такая функция всегда явно или неявно определена на этом словаре, например, некоторой таблицей соответствия. Язык состоит из бесконечного множества предложений – цепочек над его словарем. Соответствие каждого предложения его смыслу не может быть задано таблицей или заучено: это потребовало бы бесконечных ресурсов. Функция соответствия предложений языка элементам множества смыслов должна вычислять смысл предложения, как-то сочетая множество смыслов составляющих это предложение слов. Такая функция называется семантической функцией. В соответствии с гипотезой Хомского, семантическая функция вычисляется на основе дерева вывода цепочки языка в порождающей ее грамматике. Для естественных языков разрабатывается множество подходов к построению таких семантических функций, однако естественные языковые системы столь сложны, что до сих пор полного описания семантических функций для них не существует. Для искусственных языков один из простейших и в то же время мощных формализмов для задания семантических функций предложен Дональдом Кнутом [K68].
Рассмотрим рис. 3.2 б). От общей задачи трансляции рис 1.1 задача блока генерации в принципе не отличается – на входе блока генерации те же цепочки языка, правда с добавленными надстроенными деревьями вывода этих цепочек. Сложность общей задачи трансляции рис 1.1 состоит в том, что надо вычислять требуемые выходы для любой входной цепочки из потенциально бесконечного их множества, составляющего входной язык. Но и на входе блока генерации те же цепочки языка, и каждая цепочка имеет свое собственное дерево вывода (и даже, возможно, не одно!). Поэтому те же проблемы, связанные с бесконечностью количества входных цепочек, стоят и при разработке алгоритма работы блока генерации выхода. Каким же образом эти проблемы могут быть решены с использованием дерева вывода?
Пример 3.1. Рассмотрим конкретный пример - грамматику G7 арифметических выражений из Главы 2: G3.1 = G7: Е → i | (E) | E+E| E-E| E*E| E/E и дерево вывода в ней цепочки 2*(3+1) на рис. 3.3,а).:
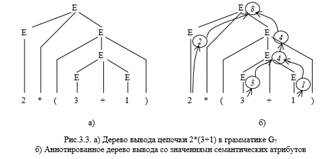
Задачей трансляции таких выражений будем считать вычисление значения выражения, полученного на входе. Искомая семантическая функция должна каждому выражению из бесконечного их множества сопоставить его значение. Естественно выполнять это сопоставление на основе структуры выражения: хотя выражений бесконечно много, но типов структур, которые могут комбинироваться в выражениях, конечное число – это сумма двух подвыражений (E+E), их произведение(EхE) и т.д. (и все они задаются грамматикой!). Свяжем с каждой нетерминальной конструкцией Е, имеющей смысл "выражение", семантический параметр (или атрибут) – значение соответствующего выражения, которое выводится из этой конструкции. Очевидно, что вычисление значения всего выражения (которое выводится из корня дерева) может проводиться последовательным вычислением значений частных подвыражений на основе их структуры. В частности, если выражение является суммой двух подвыражений, то естественно семантический атрибут (значение) этого выражения вычислять как сумму семантических атрибутов (значений) составляющих его подвыражений ( рис.3.3,б). Поэтому семантическую функцию, сопоставляющую значение каждому выражению, можно определить как последовательно вычисляемую по структуре дерева вывода, и на каждом шаге этих вычислений правила семантических преобразований атрибутов задаются семантической интерпретацией, связанной с каждым типом узла дерева вывода, иными словами, с соответствующим правилом порождающей грамматики. Итак, хотя количество возможных цепочек на входе генератора бесконечное количество, и также бесконечно число структур - деревьев вывода, которые связывает с этими цепочками блок синтаксического анализа, типов узлов в деревьях вывода цепочек конечное число, и все эти типы задаются продукциями грамматики. Семантические вычисления значения ("смысла") входной цепочки могут быть построены на основе семантических связей, которые определены для каждой продукции грамматики на основе дерева вывода, восстановленного для этой цепочки.
Будем говорить, что правила КС-грамматики имеют канонический (для РС-метода)вид, если каждая группа правил с одинаковым нетерминалом в левой части относится к одному из перечисленных ниже видов и выполняются дополнительные условия:

Если правила вывода имеют такой вид, то рекурсивный спуск может быть реализован без промежуточного построения прогнозов: для правил с несколькими альтернативами выбирается альтернатива ai i, если текущий символ совпадает с ai, иначе выбирается альтернатива, если она присутствует; если нет совпадения текущего символа ни с одним из ai и нет -альтернативы — фиксируется ошибка.
Канонический вид правил грамматики дает достаточное, но не необходимое условие применимости РС-метода. Грамматику с правилами канонического вида называют q-грамматикой. Рассмотренные выше s-грамматики являются q-грамматиками, обратное неверно.
Двусмысленные грамматики
Грамматика операторов цикла языка Милан Операторы цикла языка Милан порождаются следующей грамматикой: Gwhile: L→SS;L S →while b do L s Здесь мы абстрагировались от структуры условия (обозначив любое условие терминалом b) и от структур всех типов операторов кроме оператора цикла (обозначив их все терминалом s). Пусть в этой грамматике порождена цепочка: while b do s; s Эта цепочка имеет два различных дерева вывода (см.рис.3.12.). Как терминалы, так и нетерминалы снабжены здесь индексами, чтобы иметь возможность идентифицировать их.
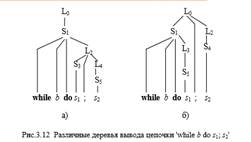
Поскольку семантические вычисления основываются именно на дереве вывода, очевидно, что различные деревья вывода могут привести к различным интерпретациям этой цепочки. Пусть семантический параметр, сопоставленный каждому нетерминалу грамматики – это блок последовательных вычислений с одним входом и одним выходом. Терминалу s сопоставим простейший блок (например, будем его интерпретировать, как оператор присваивания). Тогда каждому синтаксическому правилу (продукции) можно очевидным образом сопоставить семантические правила получения структуры сложного блока (соответствующего левой части продукций) из более простых (рис.3.13 ).
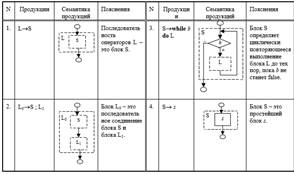
Грамматика условных операторов
Очень похожая ситуация с грамматикой, задающий условный оператор в языке Милан. Для простоты будем считать, что в условном операторе может встретиться только оператор, а не список операторов. Соответствующая грамматика определяется так: Gif: S→ if b then S else S if b then S оп Очевидна семантика этих правил. Таблица, ставящая в соответствие каждой продукции семантическое правило, представлена ниже.
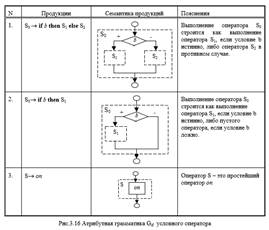
Оказывается, эта грамматика двусмысленна. Например, для цепочки: if b1 then if b2 then оп1 else оп2 можно построить два дерева вывода. Эти деревья вывода определяют различную интерпретацию этой цепочки в соответствии с семантическими правилами рис.3.16 одно из возможных деревьев вывода представлена на рис. 3.17. В соответствии с ним вся цепочка, рассматриваемая как один оператор S0, представляет собой полный условный оператор if b1 then S1 else S2. Оператор S1 в этом операторе, в свою очередь, является сокращенным условным оператором if b2 then S 3, в то время как операторы S 2 и S 3 – это простейшие атомарные в данной грамматике операторы оп1 и оп2 соответственно.
