Математические формулы и функции в Excel

Обработка данных, хранимых в ячейках рабочих листов Excel, осуществляется по формулам, определённым пользователем. Для перехода в режим создания формул необходимо выделить ячейку и ввести знак =. В формулах могут использоваться как стандартные арифметические операторы, так и встроенные функции Excel. Пример определения простейшей формулы: = (7 – 4) ´ 2.

При создании формул Excel для вычисления математических выражений руководствуются следующими традиционными правилами, определяющими приоритет выполнения операций:

– в первую очередь вычисляются выражения внутри круглых скобок;

– определяются значения, возвращаемые встроенными функциями;

– выполняются операции возведения в степень (^), затем умножения (*) и деления (/), а после – сложения (+) и вычитания ( – ).

Необходимо отметить, что операции с одинаковым приоритетом выполняются слева направо.

В Excel имеется целый ряд встроенных математических функций, существенно облегчающих решение задач. Синтаксис функций:

<Имя Функции><(Аргумент 1;...;Аргумент N)>.

Здесь в качестве аргумента могут использоваться как непосредственное значение, так и идентификатор ячейки.

При использовании в функции нескольких аргументов они отделяются один от другого точкой с запятой. Например, формула

=ПРОИЗВЕД(А1;В2;С4)

указывает Excel, что необходимо перемножить числа в ячейках А1, В2 и С4. Однако любой аргумент может быть диапазоном, содержащим произвольное число ячеек листа. Например, функция

=ПРОИЗВЕД(А 1: A3 ;В2:В4)

имеет два аргумента, но перемножает содержимое шести ячеек. Аргументы не обязательно должны образовывать непрерывные диапазоны ячеек:

=ПРОИЗВЕД(А1 :АЗ;В2;В4:В7).

Подбор параметра

Подбор параметра является удобным средством для решения задач, которые имеют точное целевое значение, зависящее от одного неизвестного параметра. С помощью Подбора параметра можно определить значение, которое будет давать желаемый результат.

В общем виде задачи, которые могут быть решены с помощью Подбора параметра, можно представить следующим образом. Есть значение х, от которого зависит формула или цепочка последовательно зависящих друг от друга формул (рис. 1). Требуется изменить х таким образом, чтобы в конечной формуле получить заданное значение.

Зависимость
	Формула F(x)
	Формула F1(x)	Формула F2(F1(x))	…	Формула Fn(Fn-1(x))

Рис. 1. Пример зависимости формул от значения или от других формул

Чтобы воспользоваться средством Подбор параметра, нужно выбрать команду меню Сервис|Подбор параметра (в Office 2007 – Данные|Анализ «Что-если»|Подбор параметра). На экране появится окно диалога (рис. 2).

В поле Установить в ячейке нужно указать ячейку, в которой находится конечная формула. Обычно, прежде чем обращаться к средству Подбор параметра, выделяют ячейку с формулой. В этой ячейке нужно получить некое конкретное значение. В этом случае в поле Установить в ячейке уже будет указана абсолютная ссылка на активную ячейку.

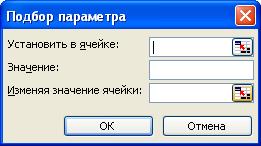
Рис. 2. Окно диалога Подбор параметра

В поле Значение нужно ввести значение, которое должно быть достигнуто в ячейке, указанной в поле Установить в ячейке.

В поле Изменяя значение ячейки необходимо ввести ссылку на ячейку, значение которой нужно подобрать таким образом, чтобы в ячейке из поля Установить в ячейке было получено значение, указанное в поле Значение. То есть в этом поле нужно указать ссылку на ячейку, значение которой является неизвестным.

Пример:

Решить уравнение х² – 1 = 0.

Квадратное уравнение имеет не более двух корней. Решение задачи включает два этапа.

1. Локализация корней. Этот этап представляет собой нахождение отрезков, на которых находится один корень.

Сделать это можно следующим образом. Сначала нужно протабули-ровать функцию на некотором отрезке [х₀; х_n]. Возможно, что выбранный отрезок не будет включать корни уравнения. Поэтому нужно построить график этой функции. При необходимости в соответствии с характером изменения функции поменять интервал исследования функции, а также шаг изменения аргумента. После этого найти либо на графике функции, либо в таблице табулирования функции отрезки, на которых функция меняет знак. За первое приближение корня можно взять середину найденного отрезка. На рисунке 3 видно, что найдено два отрезка [-1.2; 0.8] и [0.8; 1.2]. В ячейки F4 и F9 помещены начальные приближения корней на соответствующих отрезках.

Для данной задачи нужно найти два отрезка и, соответственно, определить начальные приближения для двух корней.

2. Уточнение корней. Этот этап позволит найти точное значение корней в найденных на первом этапе отрезках.

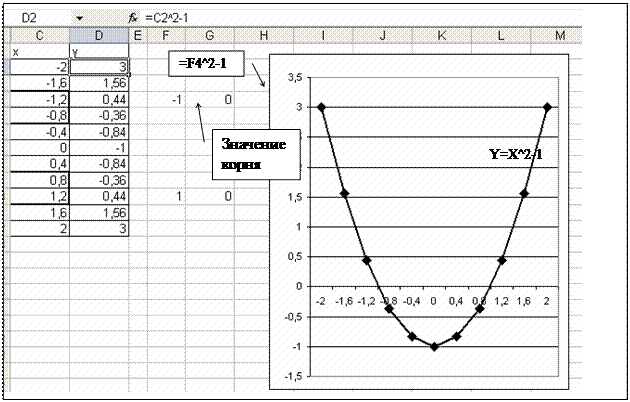Нужно вычислить значение функции в значениях, которые приняты за первое приближение корня. На рисунке 3 в ячейках G4 и G9 размещаются формулы, вычисляющие значения функции в начальных приближениях корней.

Рис. 3. Нахождение корней уравнения с помощью средств

Подбор параметра

Далее для каждого отрезка нужно применить средство Подбор параметра для уточнения корня на этом отрезке. Выделить ячейку G4, воспользоваться командой Сервис|Подбор параметра. В поле Установить в ячейке должна быть указана ссылка на ячейку G4. В поле Значение ввести значение 0. В поле Изменяя значение ячейки указать ссылку на ячейку F4. Excel найдет решение и поместит его в ячейку F4. То же самое нужно проделать для второго отрезка, чтобы найти второй корень.

В этой задаче корнями уравнения будут значения -1 и 1.