Основные структуры алгоритмов. Реализация алгоритмов.

Основные структуры алгоритмов - это ограниченный набор стандартных способов соединения отдельных блоков или структур блоков для выполнения типичных последовательностей действий. Эти структуры следует использовать, если алгоритмы (и, следовательно, программы) разрабатываются в рамках структурного подхода. Иначе, структурный подход к программированию предполагает использование только нескольких основных структур, комбинация которых дает все многообразие алгоритмов.

Элементарные шаги алгоритма при укрупнении объе­диняются в алгоритмические конструкции: последова­тельные, ветвящиеся, циклические, рекурсивные. В 1969 году Эдсгер В. Дейкстра в статье "Структуры данных и алгоритмы" доказал, что для записи любого алгоритма достаточно трех основных алгоритмических конструкций: последовательных, ветвящихся, циклических. (Бойм и Якопини (Bohm, Jacopini, 1966), Миле (Mills, 1972))

Главная идея этого доказательства сводится к тому, что необходимо преобразовать каждую часть программы в одну из трех основных структур или их комбинацию так, чтобы неструктурированная часть программы уменьшилась. После достаточного числа таких преобразований оставшаяся неструктурированной часть либо исчезнет, либо станет ненужной.

Доказательство относится лишь к простым программам, которые содержат единственный вход и единственный выход, не содержат бесполезных (недостижимых) фрагментов, не содержат бесконечных циклов.

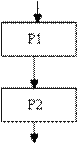
Определение.Алгоритм Р реализован через после­довательную алгоритмическую конструкцию,если каждый шаг алгоритма Р выполняется один раз, причем после каждого i-го шага выполняется ( i +1)-й шаг, если i-й шаг — не конец алгоритма.

Т.е. следование- это последовательное размещение блоков и групп блоков.

Определение.Алгоритм Р реализован через ветвя­щуюся алгоритмическую конструкцию,если от вход­ных данных зависит, какие шаги алгоритма будут выпол­няться (последовательность выполнения шагов алгорит­ма зависит от входных данных). При каждом конкрет­ном наборе входных данных ветвящаяся алгоритмиче­ская конструкция сводится к последовательной алгорит­мической конструкции.

Т.е. разветвление применяется, когда в зависимости от условия требуется выполнить либо одно действие, либо другое.

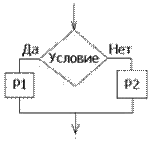
На рисунках P1 и P2 представляют собой в общем случае некоторые серии команд для соответствующего исполнителя. В зависимости от истинности (Да) или ложности (Нет) условия управление передаётся по одной из двух ветвей.

Обход- частный случай разветвления, когда одна ветвь не содержит ни каких действий.

Множественный выборявляется обобщением разветвления, когда в зависимости от значения переменной выполняется одно из нескольких действий.

Определение.Алгоритм Р реализован с использова­нием циклической алгоритмической конструкции,если некая, подряд идущая группа шагов алгоритма мо­жет выполняться несколько раз в зависимости от вход­ных данных. Любая циклическая алгоритмическая кон­струкция содержит в себе элементы ветвящейся алгорит­мической конструкции.

Т.е. если некоторая часть программы выполняется многократно и после проверки некоторого условия в какой-то момент времени осуществляется выход из нее, то такую часть программы называют циклом.

Тело цикла - та последовательность действия, которая выполняется многократно (в цикле).

Цикл «До» применяется при необходимости выполнить какие-либо вычисления несколько раз до выполнения условия.

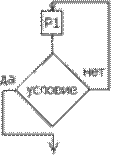
Особенность в том, что он выполняется хотя бы один раз, т.к. первая проверка условия выхода из цикла происходит после того, как тело цикла выполнено.

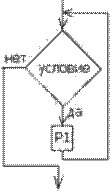
Цикл «Пока» отличается от цикла «До» тем, что проверка условия производится до выполнения тела цикла. В этом случае, если при первой проверке условия оно выполняется, то тело цикла не выполняется ни разу. Поэтому цикл «Пока» называют циклом «с предусловием», а цикл «До» - «с постусловием».

Определение.Алгоритм R называется рекурсив­ным,если на каком-либо шаге он прямо или косвенно обращается сам к себе.

Особенностью всех алгоритмических структур является то, что они имеют один вход и один выход и могут соединяться друг с другом в любой последовательности. Каждая структура может содержать в качестве одного из блоков любую другую структуру.

Вопросы для активизации и создания проблемной ситуации.

1. Что понимается под стратегией решения задач?

2. Понятие алгоритма

3. Что понимается под поиском решений задач?

4. Свойства алгоритма.

5. В чем заключается свойство массовости?

6. В чем заключается свойство конечности?

7. В чем заключается свойство результативности?

8. Какие стратегии реализации алгоритма существуют?

9. На какие виды подразделяются алгоритмы?

10. Способы записи алгоритмов

11. Графический способ записи алгоритмов.

12. Какие виды блок- схем существуют?

Лекция №10. Реализация алгоритмов. Основные вычислительные алгоритмы. (1 час)

Цель лекции: Изучить историю возникновения теории алгоритмов; принцип

работы абстрактных вычислительных конструкции; рассмотреть

принцип действия Машины Тьюринга. Сделать анализ алгоритмов;

дать понятие сложности алгоритма.

Вопросы лекции:

1. Основные вычислительные алгоритмы.

2. Машина Тьюринга.

3. Анализ алгоритмов. Понятие сложности алгоритма

4. Сопоставление алгоритмических моделей

Содержание лекции: