Игры с полной информацией, с двумя участниками

В настоящей главе рассматриваются игры, которые относятся к играм с полной информацией, с двумя участниками. В качестве примеров игр такого типа можно на­звать шахматы, шашки и го. В этих играх два игрока делают ходы поочередно и имеют полную информацию о текущей ситуации в игре. Таким образом, этому опре­делению не соответствует большинство карточных игр. Игра заканчивается после то­го, как достигается позиция, которая оценивается по правилам игры как заключи­тельная, например мат в шахматах. Правила определяют также, каким является ре­зультат игры после ее завершения в заключительной позиции.

Подобная игра может быть представлена в виде дерева игры. Узлы такого дерева соответствуют ситуациям игры, а дуги — ходам. Первоначальная ситуация игры представляет собой корневой узел, а листья дерева соответствуют заключительным позициям.

В большинстве игр такого типа результатом игры может стать победа, поражение или ничья. Но в данной главе рассматриваются игры только с двумя результатами:

победа и поражение. Б тех играх, где возможна ничья, результаты также можно све­сти к двум ситуациям: победа и отсутствие победы. Двух участников рассматривае­мых игр принято называть своим игроком и чужим игроком. Свой игрок может вы­играть в незаключительной позиции своего хода, если имеется допустимый ход, ве­дущий к выигранной позиции. С другой стороны, не заключи тельная позиция чужого хода является выигрышной для своего игрока, если все допустимые ходы ведут от этой позиции к выигрышным позициям. Эти правила соответствуют представлению задач в виде деревьев AND/OR, которые рассматривались в главе 13. В табл. 22,1 показано соответствие между понятиями, которые применяются при описании де­ревьев AND/OR и игр.

Таблица 22.1, Соответствие между понятиями, которые применяются при описании игр и деревьев «ID/OR

Игры

Деревья AND/OR

Игровые позиции

Завершающая выигранная позиция Завершающая проигранная позиция Выигранная позиция Позиция своего хода Позиция чужого хода

Проблемы Целевой узел, тривиально решаемая проблема Неразрешимая проблема Решенная проблема Узел OR Узел AND

Очевидно, что для организации поиска в деревьях игры можно применить многие понятия, которые обеспечивают поиск в деревьях AND/OR.

Простая программа, позволяющая определить, является ли выигрышной некото­рая позиция своего хода, приведена ниже.

won( Fos) :-

terminalwonf Pos}. % Заключительная выигранная позиция

won( Pos) :-

not termiriallost ( Pos),

move( Pos, Posl}, not ( move I Poslf not won( Pos2)). Правила игры встроены в

% Допустимый ход, ведущий к позиции Posl Pos2), \ Ни один ход противника не ведет

% к невыигрышной позиции

предикат raove ( Pos, Posl), который вырабатывает допустимые ходы, и в предикаты terTrdnalwon ( Pos) и terminallost ( Pos), предназначенные для распознавания заключительных позиций, являющихся выиг­рышными или проигрышными согласно правилам игры. Последнее из приведенных выше правил гласит, что не существует чужого хода, который ведет к невыигрыш­ной позиции, поскольку в этом правиле используются два оператора отрицания. Иными словами, в ситуации выигрыша все чужие ходы должны вести к выигрыш­ной позиции.

Как и другие аналогичные программы поиска в графах AND/OR, приведенная выше программа основана на использовании стратегии поиска в глубину. Кроме того, эта программа не предотвращает циклический переход от одной позиции к другой. Это может вызвать проблемы, поскольку правила некоторых игр не исключают воз­можности повторения позиций. Но такое повторение часто только внешне выглядит как результативное продолжение игры, а в действительности служит признаком без­выходной ситуации. Например, по правилам шахмат после троекратного повторения позиции в игре может быть объявлена ничья.

Приведенная выше программа демонстрирует лишь основной принцип. Но для практической реализации программ ведения таких сложных игр, как шахматы или го, необходимы гораздо более мощные методы. Из-за большой комбинаторной слож­ности этих игр приведенный выше примитивный алгоритм поиска, который останав­ливается только в заключительных позициях игры, становится полностью непршод-

Глава 22. Ведение игры

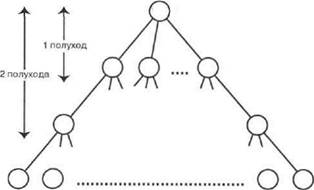
там. На рис. 22.1 эта мысль иллюстрируется применительно к шахматам. Простран­ство поиска астрономических размеров в дереве этой игры включает приблизительно 10^1И> позиций. Иногда можно услышать такие возражения, что в различных местах дерева, показанного на рис. 22.1, встречаются одинаковые позиции. Тем не менее доказано, что количество различных позиций на шахматной доске намного превосхо­дит возможности любых компьютеров, которые могут быть созданы в обозримом бу­дущем.

начальная позиция

- 30 позиций продолжения

80 полухвдов - 40ХОДЗМ

30x30 ЮООпОЗииий

- 1000*¹ позиций

Рис. 22.1, Сложность деревьев игр в шахматах. Приведенные здесь оценки основа­ны на предположении, что из любой шахматной позиции может быть сделано приблизительно 30 допустимых ходов, а заключительные позиции возникают на глубине 40 ходов. Каждый ход состоит из 2 полуходов (по 1 полуходу от каждого участника)

Проект

Напишите программу ведения какой-то простой игры (такой как ним.) с использо­ванием прямолинейного подхода, основанного на поиске в графе AND/OR,