Циклы с неизвестным числом повторений
В циклах с неизвестным числом повторений используются, как правило, операторы repeat-untilи while-do.
Табулирование функции
Пример 12. Табулировать функцию y=2x-sin(x) на отрезке [xmin,xmax] с шагом Dx, т.е. вычислить таблицу значений функции y(x), если x задан на отрезке [xmin,xmax].
В данном примере для организации циклического процесса будем использовать оператор repeat-until.
Общий вид оператора repeat-until:
Repeat
оператор1;
оператор2;
…
операторn;
until логическое_выражение;
Выполнение оператора repeat-until:
1) выполняются операторы цикла;
2) если значение логического_выражения равно true(истина), происходит выход из цикла, в противном случае процесс повторяется, начиная с пункта 1).
Программа Схема алгоритма
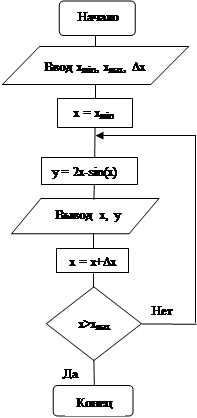 Program Prim12;
Program Prim12;
var
x, y, xmin, xmax, dx : real;
begin
writeln('Введите xmin,xmax,dx');
readln(xmin,xmax,dx);
x:=xmin;
repeat
y:=2*x-sin(x);
writeln('x=', x:7:2, ' y=', y:7:2);
x:=x+dx;
until x>xmax;
end.
Исходные данные: Результат:
xmin = -2; xmax = 1; dx = 0.5 x= -2.00 y= -3.09
x= -1.50 y= -2.00
x= -1.00 y= -1.16
x= -0.50 y= -0.52
x= 0.00 y= 0.00
x= 0.50 y= 0.52
x= 1.00 y= 1.16
Итерационные вычислительные процессы
Пример 13. Найти методом итераций корень уравнения 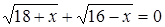 на интервале [a,b] с заданной точностью e и определить количество итераций.
на интервале [a,b] с заданной точностью e и определить количество итераций.
Указания. 1. В качестве нулевого приближения корня уравнения выберем середину интервала [a,b] (x:=(a+b)/2).
2. Для получения предыдущего и последующего приближенных значений корня уравнения будем использовать две переменные x0 и x.
3.Условие выхода из цикла: |x - x0|£e.
Программа Схема алгоритма
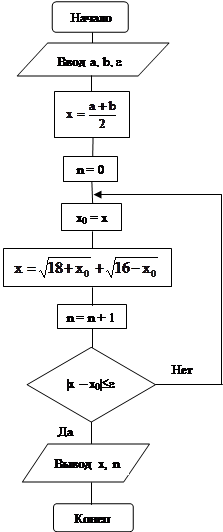 Program Prim13;
Program Prim13;
var
a,b,x,x0,eps : real;
n : integer;
begin
writeln('a,b,eps');
readln(a,b,eps);
x:=(a+b)/2;
n:=0;
repeat
x0:=x;
x:=sqrt(18+x0)+sqrt(16-x0);
n:=n+1;
until abs(x-x0)<=eps;
writeln('x=', x:8:5,' n=', n:3);
end.
Исходные данные: Результат:
a = 6; b = 8; eps = 0.0001 x= 7.93272 n= 5
Вычисление суммы членов бесконечного ряда
Пример 14. Найти сумму бесконечного ряда:
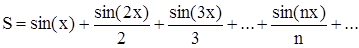
Условие выхода из цикла: |sin(nx)/n|£e
В этом примере будем использовать оператор while-do.
Общий вид оператора while-do:
Whileлогическое_выражениеdo
Begin
оператор1;
оператор2;
…
операторn;
end;
Выполнение оператораwhile-do:
Если значение логического_выражения равно true (истина), то выполняются операторы цикла, в противном случае происходит выход из цикла.
Программа Схема алгоритма
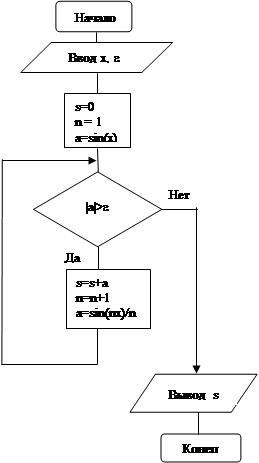 Program Prim14;
Program Prim14;
var
a,s,x,eps : real;
n : integer;
begin
writeln('Введите x, eps');
readln(x,eps);
s:=0;
n:=1;
a:=sin(x);
while abs(a)>eps do
begin
s:=s+a;
n:=n+1;
a:=sin(n*x)/n;
end;
writeln('s=', s:8:3);
end.
Исходные данные: Результат:
x = 3.48; eps = 0.0001 s= -0.168
Пример 15. Найти сумму ряда 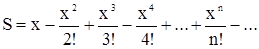
Условие выхода из цикла: |xn/n!|£e
Указания. 1. В качестве начальных приближений переменных выберем следующие значения:
s:=0; n:=1; a:=x;гдеа -очередной (текущий) член ряда.
2. Каждый последующий член ряда будем получать умножением предыдущего члена на дробь x/nи умножать на –1,т.к. ряд знакопеременный, т.е. будем вычислять по формуле:a:= -a*x/n.
Программа Схема алгоритма
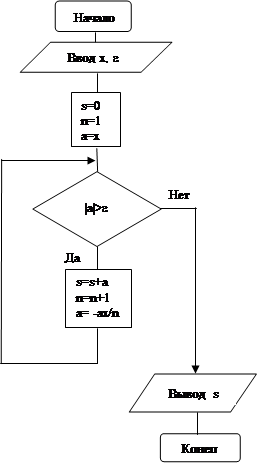 Program Prim15;
Program Prim15;
var
a,s,x,eps : real;
n : integer;
begin
writeln('Введите x,eps');
readln(x,eps);
s:=0;
n:=1;
a:=x;
while abs(a)>eps do
begin
s:=s+a;
n:=n+1;
a:= -a*x/n;
end;
writeln('s=', s:8:3);
end.
Исходные данные: Результат:
x = 1.3; eps = 0.0001 s= 0.727
Сложные циклы
Сложные циклы – это циклы, содержащие внутри себя другие циклы, называемые вложенными.
Цикл, не входящий в другие циклы, но содержащий в себе другие циклы, называется внешним циклом.
Цикл, входящий в другие циклы, но не содержащий в себе другие циклы, называется внутренним циклом.
